Nemrég logikaijáték-tervező versenyt hirdettünk, ahová manuálisan játszható egyszemélyes fejtörőket, azaz játék-prototípusokat várunk. Nemcsak ördöglakatokat, de mindenféle trükkös síkbeli és térbeli kirakót, beszuszakolós feladványt vagy szekvenciális fejtörőt is lehet küldeni szeptember 10-ig. Sokan talán, ha van is egy jónak tűnő ötletük, esetleg visszariadnak attól, hogy fabrikáljanak és saját kezűleg elkészítsék, hogy aztán tesztelni tudják a játékot.

A tesztelés hosszabb folyamat is lehet, amikor az ember újabb és újabb változatokat készít és próbál ki. Ezt a folyamatot nagyban megkönnyítheti egy program, ami virtuális térben szimulálni tud egy játékot. A Burr Tools nevű program egy ilyen ingyenes eszköz, amelyben nemcsak tervezni lehet, de a program képes az összes megoldás megkeresésére is, így nagyon le tud rövidülni a játéktervezés folyamata. A Burr Tools nagyon egyszerűen használható, ráadásul futtatható Windows, OSX és Linux operációs rendszer alatt is, így mindenkinek rendelkezésére áll, és ha elégedettek vagyunk azzal, amit alkottunk, akár 3D nyomtatásra alkalmas formában is el tudjuk menteni a játék alkatrészeit.

A program limitációja, hogy valamilyen rácshoz kötött a tervezés folyamata, de nem csak kockarácson, hanem rengeteg másfajta rácson is dolgozhatunk, ezáltal a térbeli logikai fejtörőknek egy nagyon nagy tárháza lefedhető vele. Rengeteg játéktervező használja, az alábbi síkbeli feladvány is ezzel készült, de a programmal sokkal bonyolultabb térbeli játékok is készíthetők. Biztatunk mindenkit a kipróbálására és a játéktervező versenyen való részvételre. A program használatához a YouTube-on találhattok magyar nyelvű tutorial videókat is a verseny egyik zsűritagja, Gál Péter csatornáján.

183. feladvány: Két qubittel kitölteni

Tekintsünk az alábbi poliomonó elemkészletből két szettet, azaz összesen tíz darab betűt, amelyek összesen 54 egységnégyzetnyi területtel rendelkeznek. A sárga i betűt tekintsük egyetlen merev elemnek, azaz az i betűn lévő 1×1-es pöttyöt az alatta lévő 2×1-es téglalappal együtt tudjuk csak mozgatni. Minden elem forgatható és tükrözhető. Kirakható-e ezekkel az elemekkel rés- és átfedésmentesen egy 5×11-es téglalap, amelynek pontosan a közepéről hiányzik egy 1×1-es négyzet?

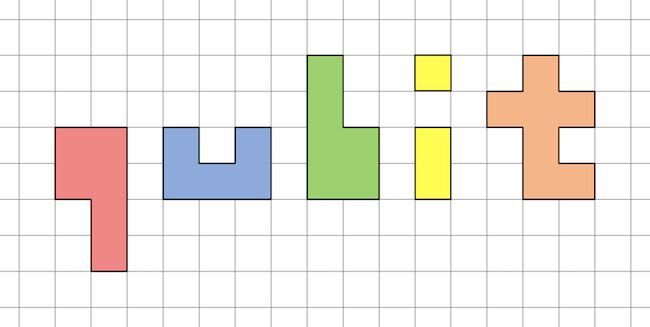
Bónusz kérdés haladóknak: Hány különböző megoldás létezik az 5×11-es téglalap forgatásától és tükrözésétől eltekintve? A közepe helyett hol hagyhatnánk még ki a téglalapból egységnyi lyukat úgy, hogy a téglalap kitölthető legyen a fenti elemekkel?

Nehézségi szint:

A megfejtéseket részletes magyarázattal és a szükséges ábrákkal együtt az eszventura@qubit.hu címre várjuk. A leggyorsabb és legkreatívabb megoldást küldő versenyzőink felkerülnek az Ész Ventura dicsőségfalára – közöttük és minden jó megoldást beküldő versenyző között év végén nyereményeket sorsolunk ki. A versenyről minden tudnivaló megtalálható: itt. Az e-mail subject mezőjében kérjük sorszámmal jelezni, hogy melyik feladvány megoldásáról van szó. Beküldési határidő: július 10. éjfél.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, kognitív kutató, társasjáték-fejlesztő és bűvész.

Kapcsolódó cikk a Qubiten: