177. feladványunkban azt vizsgáltuk, hogy mekkora körlapot lehet letakarni egy 1 × 2 méretű téglalap alakú bankjeggyel. A körlapot nem kellett teljesen becsomagolni, elég volt csak síkidomként lefedni, viszont a bankjegyet nem volt szabad tépni, vágni, csak hajtogatni. Egység átmérőjű kört természetesen könnyen le lehet fedni, hiszen ketttő is elfér belőle a bankjegy alatt, de lehet-e nagyobbat?

Hamar rá lehet jönni, hogy az alábbi félbehajtás vezethet esetleg a megoldáshoz, amikor a téglalap két szemközti csúcsa pont egymásra kerül, már csak ki kéne számolni, hogy ehhez mekkora kör tartozik.

A számoláshoz Oros Imre beküldőnk gondolatmenetét használjuk. Az alábbi ábrán XY jelöli a hajtást, K a beírt kör középpontját, amely kör az E pontban érinti az XY szakaszt, a keresett sugarat pedig a KE szakasz hossza adja. Mivel a BAX háromszög egyik szöge a bankjegy sarka, ezért egy derékszögű háromszögről van szó, amire felírhatjuk a Pitagorasz-tételt. A szóban forgó derékszögű háromszög BA befogója egységnyi, hiszen ez éppen a bankjegy rövidebbik oldala, a háromszög másik két oldaláról pedig tudjuk, hogy a hosszuk összege éppen 2 egység, mert a hajtás előtt ezek adták a téglalap hosszú oldalát. Ebből a két egyenletből az oldalhosszak már meghatározhatók, és BX hosszára 5/4, AX hosszára pedig 3/4 adódik.

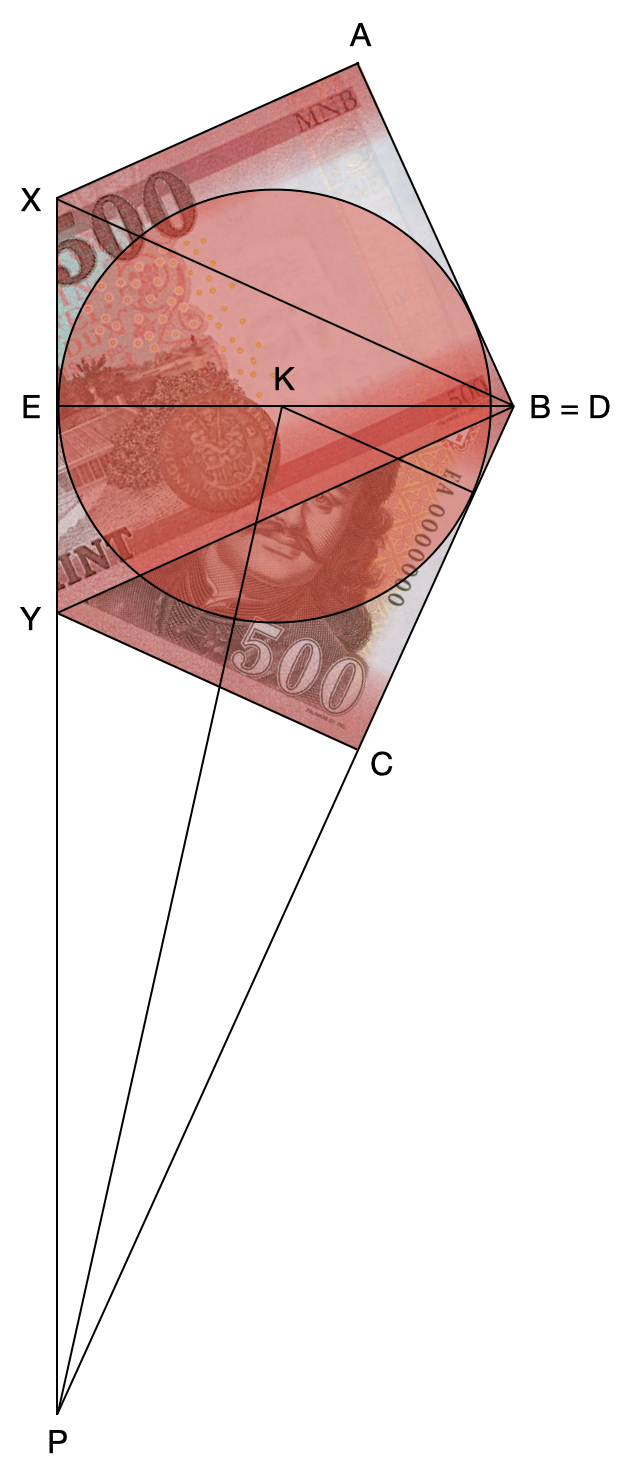
A szimmetria miatt azt is tudjuk, hogy az E pont a kihajtott téglalapnak pont a középpontja lenne, ezért BE hossza a téglalap átlójának a fele, ami √5/2. Másrészt a BEX szintén derékszögű háromszög, és ebben a háromszögben most már ismert a BX és a BE oldal hossza is, ezért az EX befogó is számolható, amire √5/4 adódik, tehát XY hossza ennek a kétszerese, azaz szintén √5/2.

Ezután vegyük fel a P segédpontot, amely a BC és XY egyenesek metszéspontja. Ekkor a PBX és BEX egymáshoz hasonló derékszögű háromszögek, mert X-ben közös szögük van. BEX háromszögnek már minden oldala ismert a PBX háromszögből viszont még csak a BX befogó ismert, a hasonlóság miatt azonban aránypárok segítségével a többi oldal hossza is kiszámítható, így PX hosszára 5·√5/4 adódik. Ebből levonva EX nagyságát PE hossza is meghatározható, amire √5 adódik.

Innen már egyszerű a dolgunk, hiszen a P-ben lévő szöget a szög szinusza alapján meg tudjuk határozni. Felhasználva a BX és PX szakaszok hosszának arányát, ami 1/√5, a szóban forgó szögre kb. 26,565 fok adódik. A keresett kör K középpontja viszont ennek a szögnek a szögfelezőjén fekszik, ezért PE hosszának ismeretében a KE sugár már számolható, amire kb. 0,5278 adódik. Ez 0,5-nél 5,56%-kal nagyobb.

Bónusz feladvány haladóknak: Továbbra is kérdés, hogy lehet-e ennél nagyobb kört lefedni? Különdíjért várjuk a számolást arra vonatkozóan, ha a két szemközti csúcs nem kerül pont egymásra, vajon akkor lehet-e nagyobb picivel a beírható kör?