Mint azt megtudhattuk, idő nincs, de óra azért még van. Így szerencsére az én feladványom se vesztette értelmét. Az volt a kérdés, hogy egy analóg órán egy nap alatt hányszor fordul elő, hogy a mutatók végpontjai egy egyenesre esnek, de semelyik két mutató nem esik egymásra.

A kismutató fél nap, azaz 12 óra leforgása alatt egyszer jár körbe, a nagymutató 12-szer, a másodpercmutató pedig ennyi idő alatt 12 × 60 = 720 kört tesz meg. A nagymutató tehát 12-szer, a másodpercmutató pedig 720-szor gyorsabban jár körbe egyenletes szögsebességgel, mint a kismutató.

Tekintsük a másodpercmutató végpontját és a kismutató végpontját összekötő egyenest. Ez mindenképpen a külső körnek egy nem elfajult húrja lesz, vagyis mindig lesz két metszéspontja a körrel, hiszen a húr átmegy a kismutató végpontján, ami a körnek egy belső pontja. A két metszéspont egyike egyébként a másodpercmutató végpontja, a másik pontot pedig nevezzük a testvérpontjának. A kérdés lényegében az, hogy a testvérpont mikor, illetve hányszor esik egybe a percmutató végpontjával úgy, hogy közben a mutatók közül semelyik kettő nem esik egymásra.

Mivel a másodpercmutató és a kismutató is mozog, bár utóbbi jóval lassabban, ezért a testvérpont is mozogni fog a külső körön, ráadásul nem is egyenletes sebességgel. A mutatók és a testvérpont mozgását úgy lehet a legpraktikusabban leírni, ha mindent a kismutatóhoz viszonyítunk, és beülünk egy olyan forgó vonatkoztatási rendszerbe, ami a kismutatóval együtt jár körbe. Ebben a rendszerben a kismutató állni fog, és csak a másik két mutató mozog. Mivel a kismutató a leglassabb, ezért a másik két mutató továbbra is azonos irányba és egyenletes szögsebességgel fog mozogni. A percmutató ebben a rendszerben fél nap alatt 11-szer, a másodpercmutató pedig 719-szer fog körbejárni, vagyis lényegében ennyiszer körözik le a kismutatót.

Most nézzük a testvérpontot. Ábrázoljuk úgy a vonatkoztatási rendszerünket, hogy a kismutató, ami ebben a rendszerben áll, legyen éppen függőleges. Ahogy a másodpercmutató halad a másodpercmutató végpontja és a testvérpont által meghatározott húr a kismutató végpontja körül forog, amit annak pillanatképei jól mutatnak az alábbi ábrán. A testvérpont sebessége ugyan változó, de a másodpercmutatóhoz hasonlóan ő is 719-szer körözi le egy nap alatt a kismutatót, és mindig azonos irányba halad.

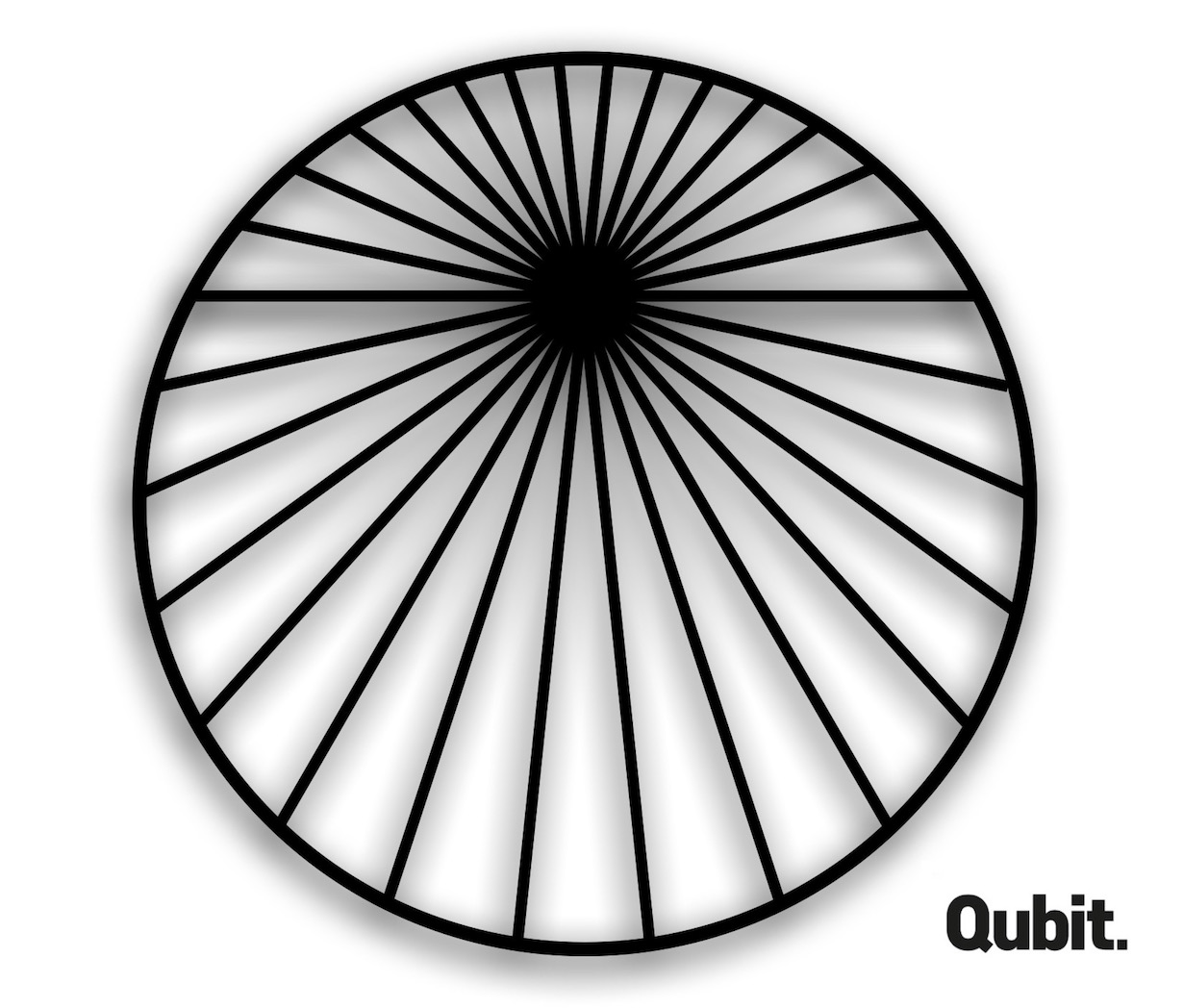
Bár erre nem lesz szükségünk, de az ábráról leolvasható az is, hogy a testvérpont sebessége akkor a legnagyobb, amikor a másodpercmutató áthalad a kismutatón, ekkor a testvérpont sebessége éppen háromszor akkora, mint a másodpercmutató végpontjának sebessége. Legkisebb pedig akkor lesz a sebessége, amikor a másodpercmutató éppen az ellentétes oldalon jár, ilyenkor a másodpercmutató sebességének csak a harmadával halad a testvérpont.

Visszatérve a lényegre, megállapítottuk, hogy fél nap alatt a testvérpont 719-szer, a percmutató pedig 11-szer körözi le a kismutatót. Ebből az következik, hogy a testvérpont 719 - 11 = 708 alkalommal esik egybe a nagymutató végpontjával, tehát ennyiszer van egy egyenesen a három mutató vége.

Mostmár csak az a kérdés, hogy hány olyan eset van ezek között, amikor két mutató egybeesik, ezeket ugyanis le kéne vonni. A két hosszabb mutató nem eshet egybe, mert a testvérpont különbözik a másodpercmutató végétől. A maradék eseteket pedig végig lehet nézni, a kismutató és a nagymutató 11 alkalommal esik egybe és 11 alkalommal esnek éppen egymással szembe, de ezekben az időpontokban a másodpercmutató sose jár éppen a közös egyenesen, kivétel az éjfél vagy a dél, de akkor mindhárom mutató egybeesik. Vagy 6:00, amikor a nagymutató és a másodpercmutató esik egybe, de ezek egyikét se számoltuk bele a 708 alkalomba. Összesen tehát egy teljes nap alatt 2 × 708 = 1416 alkalommal kollineárisak a mutatók.