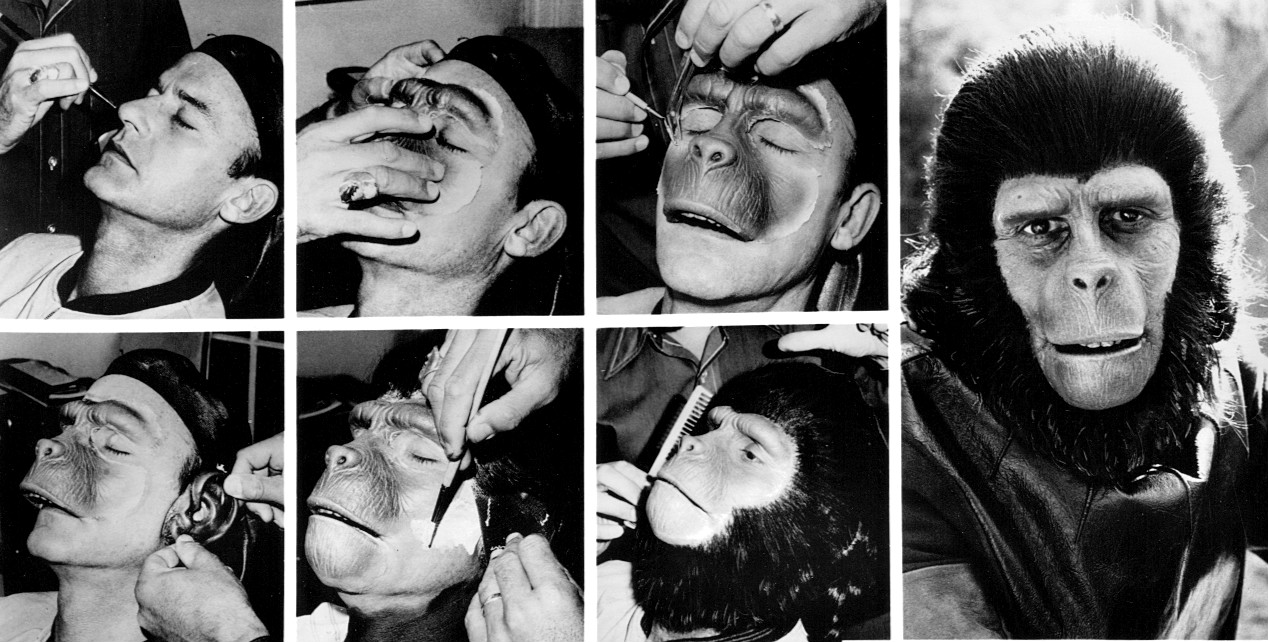
Mire képes az emberi elme, és mit nem tud a gép?

A múltkor arról volt szó, hogy az alakzatok (képek, hangok stb.) felismerése fontos része az intelligenciának, ezért a mesterséges intelligencia sokat foglalkozik az utánzásával, modellezésével. Erre sikeresen használnak például olyan mesterséges neuronhálózatokat, amilyeneket mutattam. A hálózatot arra tanítják be, hogy hasonló alakzatokra (például majmok arcképére) hasonlóképpen válaszoljanak, és másképpen, mint más alakzatokra (például emberek arcképére). A betanítás felügyelt módon történik, tehát úgy, hogy a tréning során minden alakzathoz a megoldást is megadjuk, vagyis azt, hogy milyen reakciót várunk el a hálózattól („az itt egy majom arcképe”, „ez itt egy ember arcképe”).
De a felismerés csak az egyik nagyon alapvető tényezője az intelligenciának (emberek esetében talán nem is szoktuk úgy venni, hogy különösebb intelligencia kell hozzá). Több más tényezőre és ezek együttműködésére van még szükség ahhoz, hogy igazán intelligens viselkedésről beszélhessünk. A felismerés a nyelvhasználat esetében is csak az egyik alapvető készség, amire szükségünk van, hiszen ahhoz, hogy jól használjuk a nyelvet, fel kell ismernünk a hangokat, a szavakat, a helyzeteket stb. De sok más dolog is kell hozzá.
A felügyelt tanulás során tulajdonképpen azt tanuljuk meg (vagy a hálózat azt tanulja meg), hogy miben hasonlítanak egymásra az egyikfajta ingerek (például a majomarcok), és miben másfajták (például az emberarcok). Vagyis az a tudás alakul így ki, hogy egy bizonyos szempontból mik a fontos, és mik a lényegtelen jegyei az ingereknek. Például a csecsemő már jóval a beszéd kezdete előtt meg tudja különböztetni a saját anyanyelvén (a szülei anyanyelvén) elhangzó beszédet az idegen nyelvektől, vagyis felfedezi, hogy mik az anyanyelvének a legfontosabb hangtani jellemzői. Ez is felügyelt tanulás, mert olyan, mintha minden alkalommal megmutatnánk a csecsemőnek: „így beszélnek a szüleid”; „így beszélnek mások”.
Még egy fontos tulajdonsága van annak, ahogy a múltkor az arcok felismerésének megtanulását leírtuk: az, hogy a képek tulajdonságainak önmagukban semmi értelmük sincs (mert azok olyanok, mint például a képen egy-egy pixel színe), és a tanulás végére sem alakulnak ki értelmezhető tulajdonságok ezeknek a kombinációiból. Az ilyen feladatoknál egyszerűen csak arra idomítanak be minket, hogy megtaláljuk a kapcsolatot teljesen önkényes jelkombinációk és bizonyos kategóriák (majomarc, emberarc) között. Viszont nagyon sokféle intelligens viselkedésben (és a megtanulásában) sokszor olyan tulajdonságok játszanak szerepet, amik igenis értelmesek – és feltételezhetjük, hogy ezek vagy velünk születtek, vagy korábbi tanulással jutottunk a birtokukba. És a feladat is lehet másmilyen, például az, hogy felfedezzük, milyen összefüggések vannak ezek között a tulajdonságok között. Például hogy melyikek használhatók másikak előrejelzésére (hogyan szoktak együttjárni).
A nyelvelsajátításban ilyen másféle, a felismeréstől eltérő képesség az, hogy megtanuljuk: hasonló kifejezéseket hasonló funkcióban használunk. Ezt az elvet úgy általában valószínűleg velünkszületett módon feltételezzük, része az elménk általános működésének. De hogy konkrétan az anyanyelvünkben milyen kifejezésekre lehet alkalmazni, azt meg kell tanulnunk. Például gyerekkorunkban rájövünk, hogy hogyan használják a magyarban a tulajdonságokra utaló kifejezéseket más-más szórendben jelzői és állítmányi szerepben (ez a bolond majom, viszont ez a majom bolond), míg más esetekben a szórendnek nincs ilyen súlyos jelentősége, bár persze valamilyen kevésbé látványos funkciója lehet (az öcsém megérkezett és megérkezett az öcsém). Amikor ezt úgy tanuljuk meg, hogy a szereplő tulajdonságokat már egymástól függetlenül felismerjük, akkor a feladat egészen más, mint amit az arcok vagy a betűk, számjegyek felismerésénél láttunk.
Önfelügyelt tanulás
Ha már egyszer elfogadtuk, hogy az intelligens viselkedés elsajátítása sok-sok példa alapján történik (még ha vannak is szabályok, szabályrendszerek, azok a sok-sok tapasztalatból bontakoznak ki), akkor ennek magyarázatánál a statisztika használata elkerülhetetlen. Hiszen a statisztika annak a tudománya, hogy hogyan lehet rengeteg egyedi adatot tömör formában, néhány jellemzővel megragadni. Annál a fajta tanulásnál, amikor jelenségek összefüggéseit fedezzük, fel, mint a fenti példában a szórend és a funkció összefüggését, akkor számtalan tapasztalatból általánosítunk, felfedezzük az összefüggéseiket, és így tömörebben tudjuk őket megragadni, tehát tulajdonképpen statisztikát végzünk.
Hasonló feladatokat oldanak meg akkor, amikor számtalan adatból (például a vevők vásárlási szokásaiból, elkövetett bűncselekmények adataiból stb.) tipikus mintázatokat próbálnak kinyerni, és így tipikus vásárlói, elkövetői stb. profilokat felfedezni. Sokszor az ilyet is mesterséges intelligenciának nevezik. Számtalan matematikai-statisztikai módszere van az ilyen feladatok megoldásának, és mivel az adatok tömör jellemzése a cél, ezek a módszerek közeli rokonai azoknak a tömörítési eljárásoknak, amikkel mindannyian találkozunk (ha a működésüket nem ismerjük is), amiket a file-ok tömörítésénél alkalmaznak.
A vásárlók, a bűnözők vagy a kifejezések profiljainak ismerete nem felügyelt tanulás során történik: nincs olyan előre megadható „megoldás”, mint a számjegyek, a betűk vagy az arcok felismerésénél. Ezért az ebben alkalmazott eljárásokat a szakirodalom nem felügyelt (unsupervised) tanulásnak nevezi. Én inkább önfelügyelt tanulásnak nevezném, mert ebben az esetben is van a tanulónak egy célkitűzése, amit megpróbál megközelíteni, csak ez nem kívülről származik, hanem belülről fakad. Például a nyelvi kifejezések jellemzésénél az a belső cél, hogy egyszerre hozzunk létre profilokat (olyasmiket, mint a szófajok, még ha az iskolában tanult szófajokhoz ezeknek alig lesz közük), és ezzel egyidejűleg a különböző tulajdonságokat úgy súlyozzuk, hogy minél nagyobb szerepe van egy-egy tulajdonságnak a profilokba sorolásban, annál nagyobb legyen a súlya. Így aztán a legnagyobb súlyú (legfontosabb) tulajdonságok alkalmasak a többi nagyobb súlyú (fontosabb) tulajdonságok előrejelzésére. Ezt a belső célkitűzést matematikai pontossággal meg lehet fogalmazni, és lehet tervezni olyan algoritmusokat (akár neuronhálók segítségével), amelyek megtalálják a legjobb (vagy valamelyik legjobb) megoldást.
Egy szó a vektorokról
Muszáj egy kicsit felidézni (vagy megint felidézni) az iskolai tanulmányainkból egy fogalmat, a vektorokét, mert ezek nagyon fontos szerepet játszanak a mesterséges intelligenciának ebben a részében.
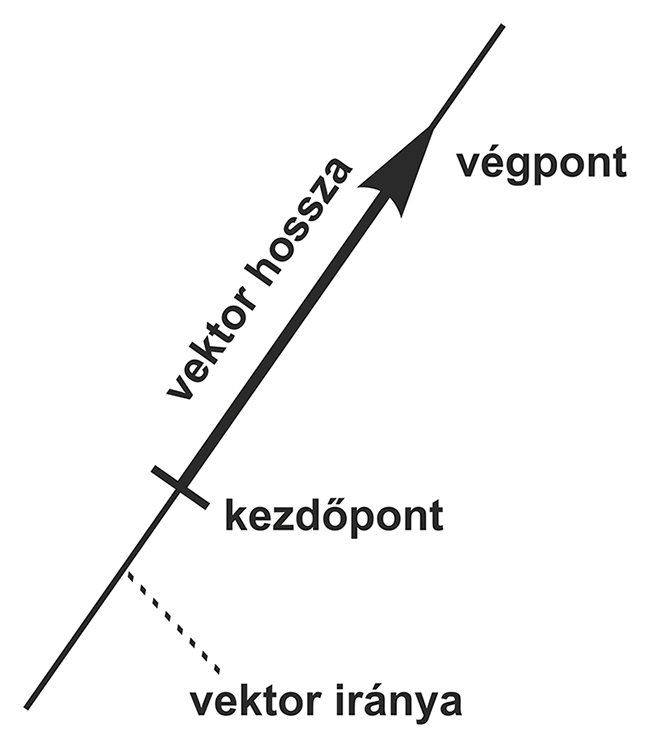
A vektor olyan lény, olyan absztrakció, amit összesen két dologgal jellemezhetünk: a hosszával és az irányával. Ezért úgy szoktuk lerajzolni, mint egy egyenes szakaszt, aminek az egyik végén egy nyíl van. Ez azért praktikus, mert a szakasznak van hossza is, meg az elhelyezkedése (a nyíllal együtt) egy irányt is kijelöl. Például ilyen vektorral szokták elvontan ábrázolni az erőket, mert azokra is egy nagyság és egy irány jellemző. Persze a szakasz és a végén a nyíl a papíron csak kétdimenziós vektort tud ábrázolni (vagy ha egy kicsit megerőltetjük a fantáziánkat, és perspektivikus ábrát rajzolunk, esetleg háromdimenziósat), ami azt jelenti, hogy a szakasz egy síkon fekszik, az iskolából ismert kétdimenziós koordinátarendszerben (x és y tengely, ugye tetszik emlékezni). Három dimenziónál meg már térről beszélünk, és van még egy ezekre merőleges (z) tengely. Például lehet olyan síkbeli vektor, ami egy négyzet átlójában húzódik, és az egyik csúcsban van a végén a nyíl, és lehet olyan (háromdimenziós) térbeli vektor, ami meg egy kocka átlójában húzódik ugyanígy.
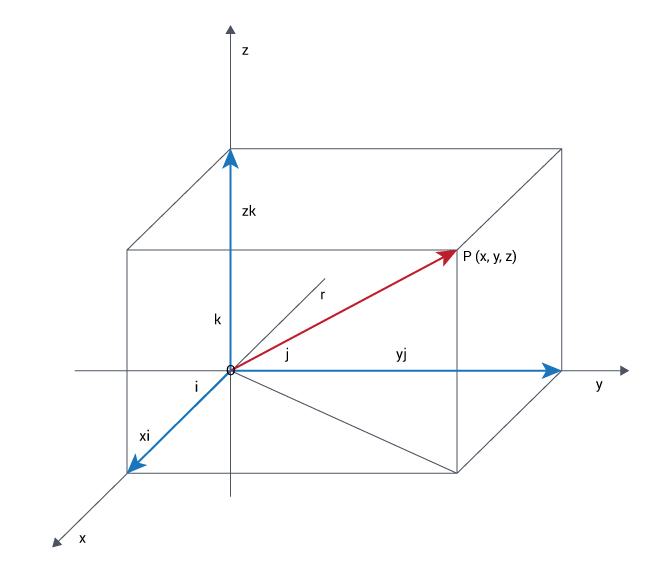
De a vektorokat nemcsak nyilakkal, hanem egy nagyon egyszerű trükk segítségével egyszerűen számsorozatokkal is ábrázolhatjuk. Ha például egy síkbeli vektort beleképzelünk az iskolából ismert koordinátarendszerbe, akkor, mivel csak az iránya és hossza számít, a koordinátarendszeren belül oda rakjuk, ahova csak akarjuk. Állapodjunk meg abban, hogy a kiindulópontját (a szakasznak azt a végét, ahol nincs nyíl) a koordinátarendszerünk origójába tesszük (a (0;0) pontba, ahol az x és y tengely metszi egymást). És akkor a vektort egyértelműen jellemzi, hogy hol a másik vége (ahol a nyíl van). Elég tehát ezt az egy pontot megadni ahhoz, hogy a vektort egyértelműen jellemezzük, márpedig ezt a pontot két számmal (az x és az y koordinátájával) megadhatjuk. Tehát a síkbeli vektorok egy két számból álló számsorral megadhatók. Ugyanígy a háromdimenziós térben meg három számból álló sorozattal adhatunk meg egy vektort (a z koordinátáját is hozzábiggyesztve). És ezt nyilván általánosíthatjuk: egy akármilyen hosszú (mondjuk n számból álló) számsorozat egy annyi dimenziós (esetünkben n-dimenziós) vektornak felel meg, még ha azt a vektort lerajzolni vagy akár nyílvessző-szerűen elképzelni nem tudjuk is.
Mi közük a vektoroknak a vásárlói meg bűnözői profilokhoz és a gépi tanuláshoz? Hát az, hogy – ahogy feljebb írtam – a vásárlók vásárlói szokásai, a felhasználók netezési, utazási vagy telefonálási szokásai, a bűnözők elkövetési szokásai mind olyan jelenségek, amik nagyon sok résztulajdonságból és részeseményből tevődnek össze, ezért rengeteg szempontból kell jellemeznünk őket. Például a vásárlónál: mikor milyen árucikkből milyen mennyiséget vett? (Ahol már maguk az árucikkek is rengetegfélék lehetnek.) Vagy például szavak esetében: milyen szövegekben milyen szavak előtt vagy után, azoktól milyen távolságra hányszor fordult elő egy bizonyos szó? (Ahol eleve szavak százezreiből áll az alaphalmaz.) Vagyis az adatok, amikből tanulni kell, amiben összefüggéseket kell észrevenni, mind nagyon hosszú, akár milliós hosszúságú számsorokból állnak, rengeteg, nagyon sok millió számsor adja ki az adatokat. Nem véletlen, hogy big data az összefoglaló beceneve az ilyen méretű adathalmazokkal foglalkozó technológiáknak.
A big datában minden a nagyon hosszú vektorokkal való bűvészkedésről szól. A big data korszaka tulajdonképpen nem az intelligenciára vonatkozó felfedezésekkel kapcsolatos. Pusztán annyi történt, hogy az 1990-es évek végétől kezdve (bár nagyon nehéz lenne időben pontosan elhelyezni a kezdetet, mert folyamatos fejlődésről van szó) eljutott odáig a számítástechnika, a hardveripar és a matematika, hogy reális lehetőséggé vált az ilyen csillagászati méretű adathalmazok kezelése és értelmes feldolgozása.
Mit tudunk kezdeni a vektorokkal?
Teljesen reménytelen lenne mindazokról a technikákról és felhasználási módjaikról röviden beszámolni, amik a big data keretében nap mint nap feltűnnek a tudományos sajtóban és néha még a népszerű médiában is. A mi szempontunkból csak az a fontos, hogy mit is csinálnak ezek a technikák, és mire jók.
Hogy nagyon leegyszerűsítsem a dolgot, a big datában a legtöbb eljárásnak az a lényege, hogy (tág értelemben vett) statisztikai eszközökkel tömörebb formában tudja ábrázolni azt a rengeteg nagyon hosszú vektort, amikről beszéltem. Egy nagy termelő vagy szolgáltató hálózat vezetői elolvadnának a boldogságtól, ha a sokmillió különböző kliensüket négy nagy csoportba tudnák osztani, amiknek a viselkedését néhány jellegzetes szokás jellemezné, mert akkor elég lenne négyfajta terméket vagy csomagot összeállítaniuk, és mindenki örülne. Ilyen radikális eredményt persze nem várhatunk, csak azért túloztam el a dolgot, hogy világos legyen, mire törekszünk.
Hogyan lehet közelebb jutni ahhoz, hogy boldoggá tegyük a megrendelőket? Egy nagyon-nagyon sok dimenziós teret, ami rengeteg vektort tartalmaz, úgy kellene ábrázolnunk, hogy a tartalma ne sokat változzon, és mégis radikálisan csökkentsük a dimenziók számát. Nagyon rossz hasonlattal olyasmire van szükség, mint a rajzolásban a perspektivikus ábrázolás felfedezése, ami lehetővé tette, hogy síkban (két dimenzióban) ábrázoljanak térbeli (háromdimenziós) tárgyakat, már amennyire ez egyáltalán lehetséges. Sok dimenzió esetén ez már-már olyasminek tűnik, amit metaforikus kifejezéssel „a lényeg kibogozásának, meglátásának” nevezhetünk. Számtalan technikája van (köztük akár olyanok is, amik a korábban már látottakhoz hasonló neurális hálókat használnak), de ezek részletei a lényeg szempontjából közömbösek.
A big data és az intelligencia
A big data segítségével elérhető eredményeket egy pillanatra sem szabad alábecsülnünk, de indokolt feltenni azt a kérdést, hogy hogyan viszonyulnak ezek az intelligenciához, vagyis hogy mennyivel visznek közelebb az emberi intelligencia modellálásához. (Ugyanezt a kérdést egyébként a korábbi „intelligens” algoritmusok esetében is rendszeresen feltették. Például nem világos, hogy az egyre jobban sakkozó gépek megalkotása hozzájárult-e valamivel az emberi intelligencia megértéséhez vagy szimulálásához. Az emberek többsége ugyanis, ha egyáltalán tud sakkozni, nem valami jó sakkozó.)
A big datában szokásos eljárások mindenképpen sok szempontból az intelligens viselkedéshez hasonló jegyeket tudnak mutatni. Például a dimenziók közötti összefüggések feltárása révén osztályozni tudjuk a vektorokat (illetve ezeken keresztül például a vásárlókat), meg tudjuk állapítani, hogy mik a vásárlásaik legfontosabb törvényszerűségei, sajátosságai. Ez még bizonyos jóslatok megtételére is alkalmas, például ha bizonyos termékek megvásárolását mások megvásárolása szokta követni, akkor abból, hogy valaki az egyiket megvette, valamilyen biztonsággal megjósolhatjuk, hogy a másikat is meg fogja. Márpedig az osztályozás (szakszerű szóval: kategorizálás) meg a jóslás (szakszerű szóval: predikció vagy anticipáció) nagyon fontos részképességei az intelligenciánknak.
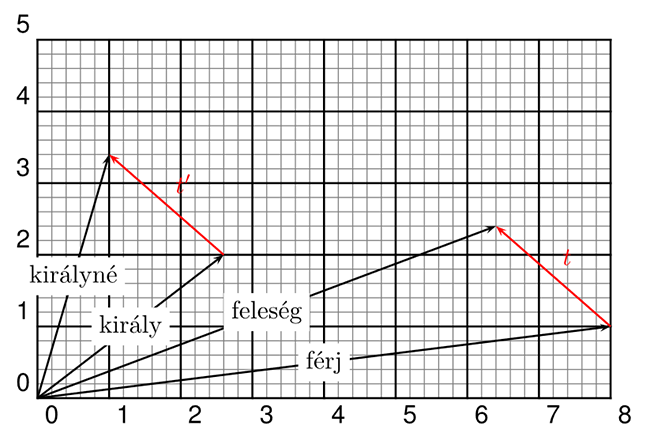
Sőt, még olyan látványos teljesítményekre is képes a big data, mint analógiák felfedezése, ami úgy általában egy igen magas szintű gondolkodási képesség. Igaz, hogy egyelőre csak elég egyszerűeket vagyunk képesek felfedezni. Például ha a férj és a feleség szót azokkal a vektorokkal jellemezzük, ami a milliónyi előfordulásuk környezetéből adódik (milyen más szavak előtt és után, tőlük milyen távolságra, milyen szövegekben, hányszor stb.), és megnézzük, hogy ezek között a vektorok között milyen a matematikai viszony (milyen transzformációval lehet az elsőből a másodikat megkapni), akkor azt fogjuk tapasztalni, hogy mondjuk a király és a királyné vektorai nagyjából ugyanabban a transzformációs viszonyban állnak egymással. Vagyis fennáll az az aránypár (analógia), hogy a férj úgy viszonyul a feleséghez, mint a király a királynéhez.
Ugyanakkor nagyon jelentős képességek utánzásától még nagyon távol állunk, és nem is világos, hogy a big data keretein belül fogunk-e a közelükbe jutni. Például éppen ahhoz, ami a korábbi, klasszikus mesterséges intelligencia középpontjában állt, a logikus gondolkozáshoz, bonyolult következtetési láncok végigviteléhez egy cseppet sem vitt közelebb a big data. De van olyan képesség is, amivel a korábbi típusú mesterséges intelligencia sem tudott igazán mit kezdeni, és a big data sem. Ilyen az, amire a korábbi cikkben már utaltam: viszonylag jól tudjuk utánozni az orvosi tudásnak azt a részét, hogy felállítsunk egy diagnózist (a korábbi esetekhez való hasonlóságok alapján), de alig értünk valamit abból, hogy a korábbi (sikeres) kezelések részleteiből hogyan kellene az aktuális helyzethez alkalmazkodó új kezelést szintetizálni. Ugyanez a probléma a gépi fordítással kapcsolatban is felvetődik. Annak ellenére, hogy kiválóan fel tudjuk ismerni, hogy mások korábbi fordításaiban mi minek felelt meg (akár a szövegek jellegétől függően is), a gyakorlatban jól érezhető, hogy új fordítások szintetizálásakor még mindig minden algoritmus csikorgó, sokszor teljes „félreértéseket” tartalmazó eredményekkel áll elő.
Végül még valami, ami talán össze is függ az előző hiányosságokkal. A big data legtöbb algoritmusa nyilvánvalóan nem felel meg semmi olyannak, ami az emberek agyában történik, különösen a tudás megszerzését (például a nyelv elsajátítását) illetően. Van ugyan néhány próbálkozás arra, hogy a rengeteg adatot apránként adagolva, ún. inkrementális módszerrel fokozatosan építgessék az automatikusan megszerzett tudást, ezek még nagyon gyerekcipőben járnak. Pedig én nagyon is elképzelhetőnek tartom, hogy az intelligencia megértésének és modellálásának a kulcsa az lenne, hogy megértjük, hogyan alakul ki, persze bizonyos születéstől adott alapképességek felhasználásával.
A szerző nyelvész, az MTA Nyelvtudományi Intézetének főmunkatársa. A Qubit.hu-n megjelent írásai itt olvashatók.
Kapcsolódó cikk a Qubiten: