Ész Ventura: Végignézted mind a 75494 állapotot a kétfős feladvány megoldásához?

Az Ész Ventura kétszemélyes q betűs játékával kapcsolatban több kérdést is felvetettünk. Aki viszont játszani is szeretné ezt a játékot, annak az a leginkább érdekes kérdés, hogy van-e valamelyik játékosnak nyerő stratégiája, és ha igen, akkor az mennyire bonyolult.
Ha egy játékban létezik nyerő stratégia, és nem olyan bonyolult, hogy a nyerő stratégiát ne lehessen kiokoskodni és/vagy megjegyezni, akkor az a játék nem lesz túl érdekes miután a játékosok kiismerték. Ha pedig nincs ugyan stratégia, amivel minden esetben nyerni tudunk, akárhogy is lépjen az ellenfél, de van egyszerűen követhető nem vesztő startégia, amivel döntetlenre lehet kihozni vagy végtelen sokáig el lehet húzni egy játékot, akkor megintcsak nem túl szórakoztató a játék.
Sakk és tic-tac-toe
A sakk is olyan játék például, ahol bizonyítható, mint általában minden véges állapotterű páros játék esetében, hogy a világos kezdő játékos számára vagy van nyerő stratégia, vagy van nem vesztő stratégia, esetleg a sötétnek van nyerő stratégiája, csak sajnos senki nem tudja, hogy melyik az igaz, sem azt, hogy konkrétan mi lenne az a stratégia, vagyis miket kell lépni.
Ennek pedig az az oka, amiről korábban már írtam, hogy a sakk lehetséges állapotainak a száma olyan nagy, hogyha nanoszekundumonként vizsgálnánk meg egy állást, akkor is 10^34 másodpercig, azaz 10^26 évig tartana az összes lehetséges állás végignézése, ami az Univerzum életkorának is rengetegszerese. Ezért tud a sakk érdekes játék lenni, amiből világbajnoságokat is érdemes rendezni.
Ezzel szemben mondjuk egy tic-tac-toe játék olyan primitív, hogy fejben is bárki ki tudja kalkulálni a lehető legjobb lépést, amivel legalább döntetlenre kihozható, ha viszont az ellenfél is megfelelően játszik, akkor nyerni nem lehet benne, ezért elég unalmas. Tic-tac-toe-világbajnokságot tehát ostobaság lenne rendezni, bár módosított verziójából tudtommal már rendeztek.
75494 állapot a q betűs feladványban
Visszatérve a q betűs feladványukra, ez egy olyan játék, aminek épp elég nagy az állapottere ahhoz, hogy ne lehessen fejben annyira áttekinteni, hogy valaki biztosan tudja minden lépésre a helyes választ. A játék lehetséges állapotainak száma ugyanis 75494. A játék állapota alatt értjük a tábla állását, azaz a két színes q betűnek és a szürke négyzeteknek az elhelyezkedését, továbbá azt, hogy éppen melyik játékos a soros.
Ahhoz hogy kiderítsük, melyik állásból kinek van nyerő stratégiája, fel kell térképeznünk a játék állapotterét. Az alábbi illusztráción minden egyes állapotot egy színes pöttyel jelölünk, kékkel, ha a kék, és pirossal, ha a piros játékos következik. A kezdő állást s betűvel jelöltük meg. Ha egy adott állásban tud lépni a soron következő játékos, akkor az adott állapothoz tartozó pöttyből nyilak mutatnak az elérhető lehetséges állapotokba. Így tehát kék pontból csak piros pontokba, piros pontból pedig csak kék pontokba mutatnak a nyilak, hiszen a játékosok felváltva követik egymást. Ha valaki nem tud lépni, azaz nincs az adott állapotból kifele nyíl, akkor a szóban forgó játékos veszített. Az ilyen vesztes végállapotokat a nyertes játékos színével gyűrűként körülvett pöttyök jelölik.
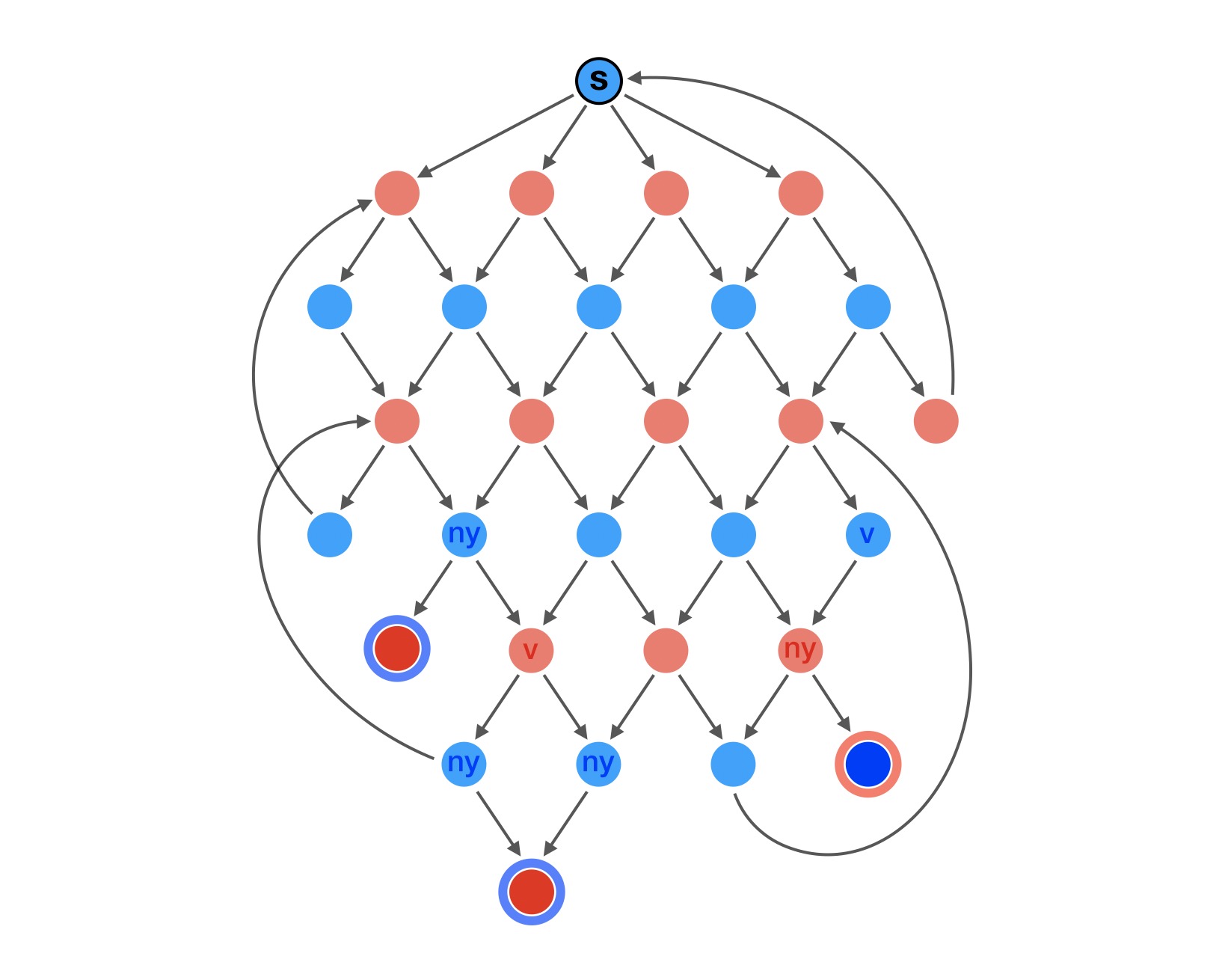
Egy ilyen állapottér ábrát tehát a sakkra nem tudnánk felrajzolni, de a q betűs játékra számítógép segítségével elkészíthető és vizsgálható a hozzá tartozó 75494 pontú irányított gráf. A fenti ábra azonban csak egy illusztráció. Ezen az illusztráción a kéknek egy, a pirosnak pedig kettő vesztes végállapota látható. Azon kék állapotok, amikből a piros egy vesztő állapotába nyíl mutat, a kék számára nyerő állapotok, hiszen onnan egy lépésben tud nyerni, ezeket kék ny betűvel megjelöltem. Hasonlóan az a piros állapot, amiből nyíl mutat a vesztő kék végállapotba, a piros számára nyerő, amit piros ny betűvel jelöltem.
Más állapotokról is eldönthető még az eddigi információk alapján, hogy kinek nyerő vagy vesztő állapotok. Ha van például olyan piros állapot, amiből csak nyerő kék állapotba mutat nyíl, akkor az sajnos a piros számára vesztő állapot, hiszen bármit lép, a kék fog nyerni (ha jól játszik). Ezeket piros v-vel jelöltem. Hasonlóan vesztő a kék számára egy olyan állapot, amiből csak nyerő piros állapotba mutat nyíl, ezt kék v-vel jelöltem az alábbi kiegészített ábrán.
Ezeket az elveket használva a gráf visszafejthető egészen a start állapotig, és eldönthető, hogy az vesztő vagy nyerő állapot a kék számára, esetleg egyik se. Lehetnek ugyanis még olyan pontok, amelyek a fenti szabályok alapján nem sorolhatók be sem vesztő, sem nyerő állapotnak; az ezek között a pontok között menő nyilakat az alábbi illusztráción narancssárgával jelöltem. Ha a játék ide keveredik, vagy innen indulna, akkor egyik játékosnak sem éri meg kilépni a narancssárga ciklusból, mert akkor a másik játékos nyerni tudna.
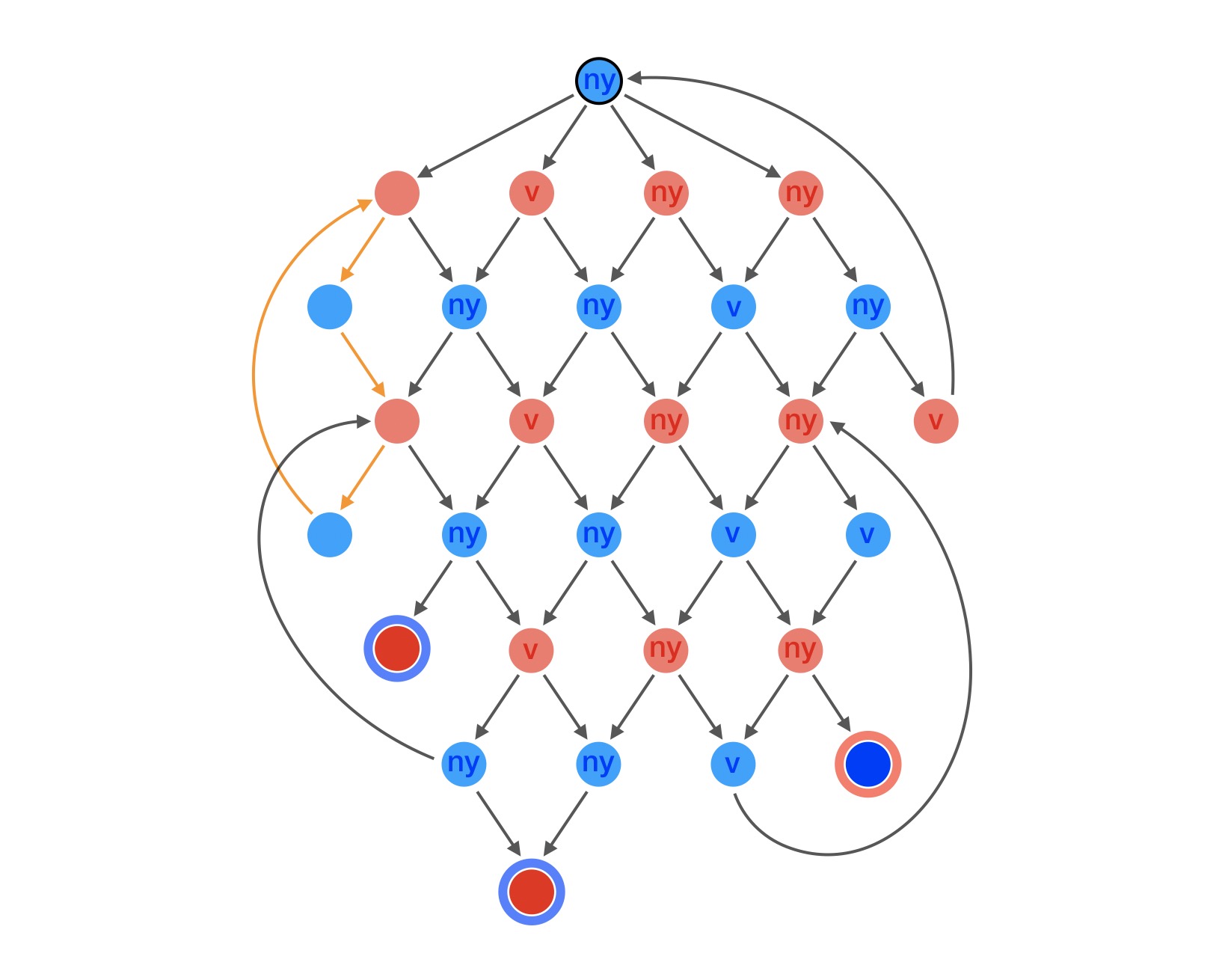
A fenti illusztárción láthatjuk, hogy ebben az egészen egyszerű esetben az állapotokat egészen a start állapotig vissza lehet fejteni, és kiderült, hogy a kéknek van nyerő stratégiája, és a játék összes lehetséges állapota közül csak négy olyan állapot van, ami se nem nyerő se nem vesztő egyik játékos számára se. A valódi q-játék 75494 pontú gráfjában azonban 21062 ilyen döntetlen állapot is van, ráadásul a feladványban szereplő kezdőállás ezek közé esik.
A döntetlen állapotok jellemzője tehát, hogy egy ilyen állapotból a játékos nem tud úgy lépni, hogy az ellenfelet vesztő állapotba kényszerítse, de mindig van lehetősége olyan lépésre, ami az ellenfelet is döntetlen állapotba viszi. Így ha mindkét játékos optimális startégiát követ, a játék sosem ér véget, egyik játékos sem tud nyerni. Gyakorlatban viszont, mivel a játék állapottere elég nagy ahhoz, hogy ne lássuk át teljesen, a cél az, hogy ne hibázzunk. Aki szeretné, Boros Péter megoldó jóvoltából a neten ki is próbálhatja a játékot.
Volt egy olyan kérdés is, hogy miért a kék kezd? Természetesen azért, mert a piros kezdése esetén a pirosnak nyerő stratégiája van, mégpedig egy lépésben, ráadásul többféle módon is, lásd az alábbi ábrát. Például a piros q-t és a felső szürke kis négyzetet egy egységnyit jobbra tolva a kék q betűje beszorul és azt sehova nem tudja már áthelyezni, lásd a bal oldalon.
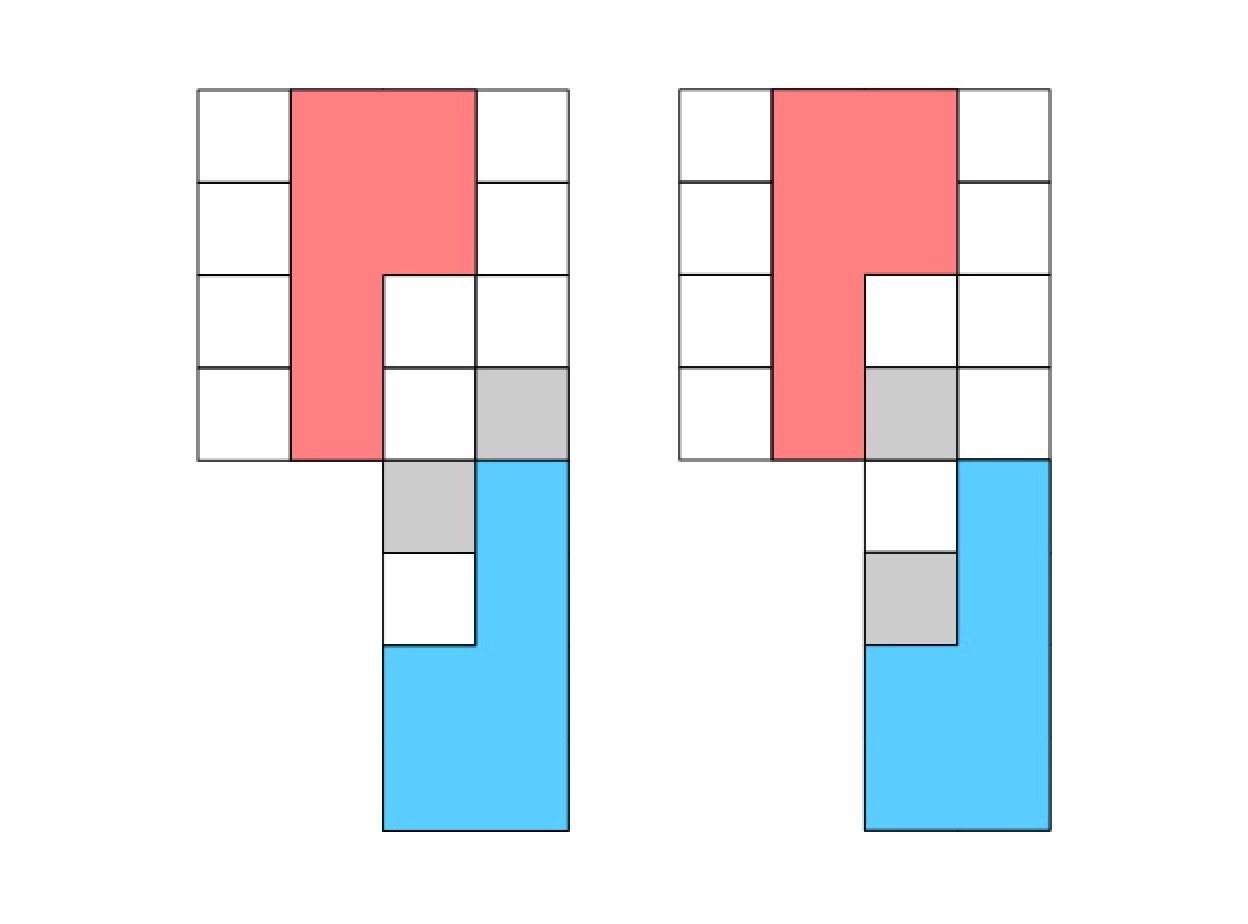
És a megoldás
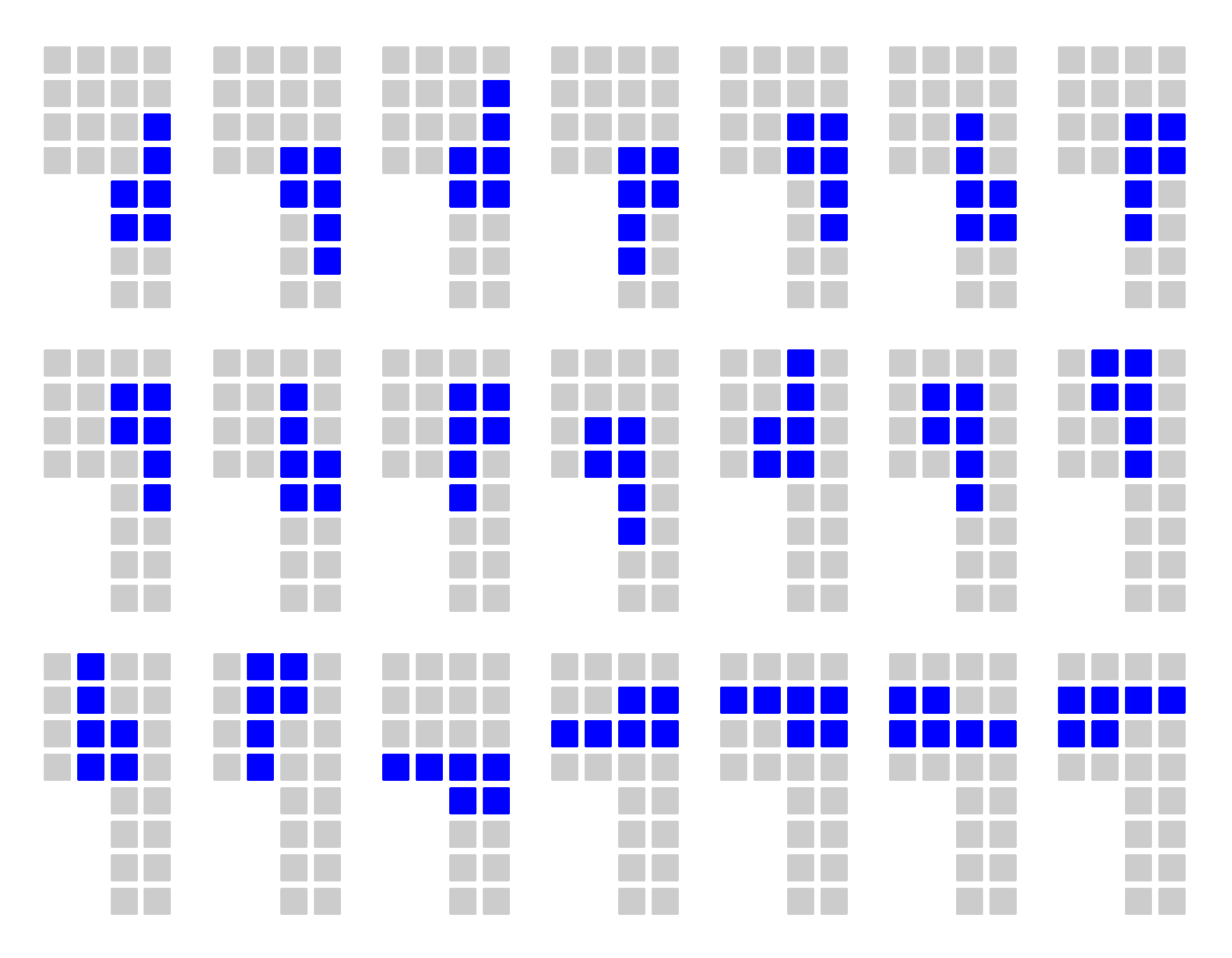
Végül térjünk rá a feladvány megoldására. A lehetséges végállapotokat, feltéve, hogy piros nem tud lépni, az alábbi ábra mutatja. Összesen 403 ilyen állás van.

Az összes lehetséges pozíció száma egy q betűre 43. Ezekből azon pozíciók száma, amelyek egy végállapotban a nyertes (fenti ábrán kékkel jelölt) játékos q betűjének pozíciói, 21 darab. Ezeket kézzel és kis türelemmel papíron is ki lehet szöszölni, nem szükséges hozzá a fenti hálózatos gondolatmenet és programozás, ha viszont valaki már számítógéppel előállította a lehetséges végállapotok fenti listáját, akkor csak szortírozni kell őket.
Kapcsolódó cikk a Qubiten:
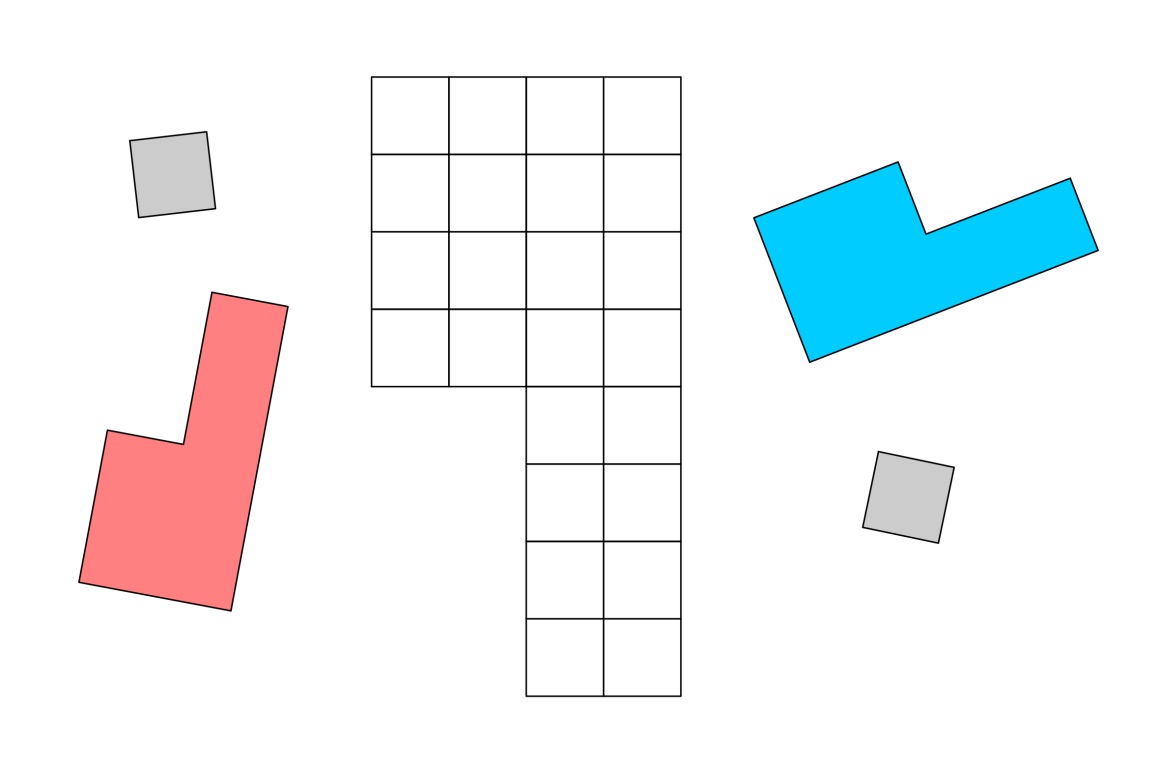
Ész Ventura: Itt a Qubit kétfős logikai játéka
Mozgassátok felváltva a q betűiteket és legfeljebb egy kis szürke négyzetet. Aki nem tudja a q betűjét áthelyezni, az veszít!
