Az élőlények és a városok közös elmélete
A fizikában hozzászoktunk, hogy képletekkel írjuk le az eldobott kő és a Nap körül keringő bolygók egyedi mozgási pályáját. Vagy a kuktában uralkodó gáznyomást, ami a sok gázrészecskének egy átlagos, statisztikai jellemzője. Megválaszolunk olyan elméleti kérdéseket, hogy elvben milyen magas lehet egy hegy a Földön és a Marson.
Törvényszerűségek és összefüggések ugyanakkor a biológiában, sőt a „városok tudományában” is ismertek. Már Galileit is foglalkoztatta az a kérdés is, hogy miért nem nőhet egy állat 200 méter magasra. A városok tudománya pedig egy új, formálódó tudományterület, amibe Geoffrey West: Scale: The Universal Laws of Growth, Innovation, Sustainability, and the Pace of Life in Organisms, Cities, Economies, and Companies című 2017-es könyve enged izgalmas betekintést.
2006 óta a Föld lakosságának több mint fele városokban él. 2050-re ez az arány eléri a 75 százalékot. Mindenki globalizációról beszél, pedig ezt a korszakot nyugodtan lehetne a hiperurbanizáció korának is hívni. A legtöbb új város ebben a pillanatban Kínában, Indiában, Dél-Ázsiában és leginkább Afrikában jön létre, vagy gyarapodik őrült sebességgel. Afrika jövője egyértelműen urbánus.
Az élőlények sejtekből épülnek fel, a városokat emberek alkotják. Látunk-e valamilyen törvényszerűséget, ha az élőlények tulajdonságait a (pillanatnyi) tömegük, a városok tulajdonságait pedig a (pillanatnyi) lakosságszám függvényében vizsgáljuk?
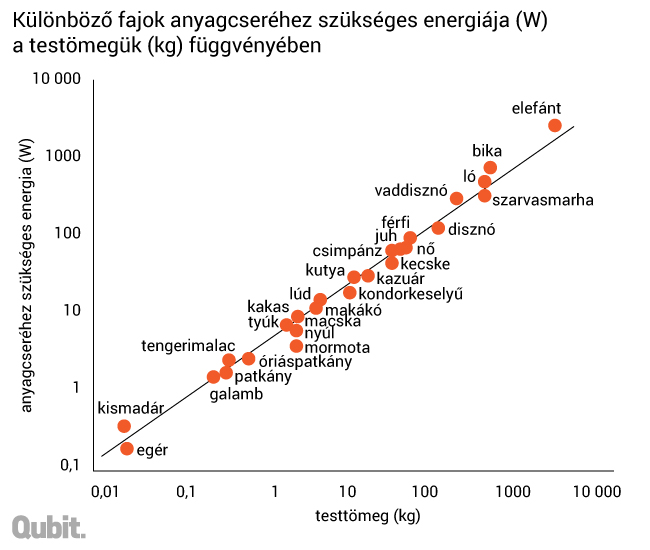
A fenti ábra vízszintes tengelyén különféle állatok tömegét látjuk az egértől az elefántig, a függőleges tengely pedig az életben maradásukhoz szükséges pillanatnyi energiamennyiséget mutatja. Az ábrázolás mindkét tengelyen logaritmikus, ami annyit jelent, hogy egy egységet a vízszintes tengelyen jobbra haladva tízszeres változást látunk tömegben, míg egy egységet a függőleges tengelyen felfelé haladva tízszeres változást látunk az energiában. Ezt az ábrázolást log-log ábrázolásnak nevezzük.
Mit mutat ez az ábra? Az ember valahol az ábra közepén van 100 kg körüli tömeggel és 100 W energiával. Egy nap mindössze annyi energiát viszünk be élelemmel, mint amennyit egy 100 wattos izzó fogyaszt, ha egész nap üzemel. Ennél lényegesebb, hogy egyrészt az ábrán a különféle állatok nem elszórtan, hanem egy egyenesre illeszkedve helyezkednek el, másrészt négy nagyságrendnyi ugrás tömegben csupán három nagyságrendnyi ugrást jelent energiában. Ezt az összefüggést nevezzük Kleiber-törvénynek. Az állatok energiát spórolnak a méretük növekedésével.
Miért szükséges a log-log ábrázolás? Ha az lenne a helyzet, hogy ugyanakkora ugrás a tömegben ugyanakkora ugrást jelentene a bevitt energiában is, akkor nem csak a log-log ábrázolásban látnánk egyenest, hanem úgy is, ha mindkét tengely a megszokott, lineáris tengely lenne. Ha a log-log skálán látható görbe meredeksége kisebb, mint 1, akkor szublineáris, ha nagyobb, mint 1, akkor szuperlineáris skálázásról beszélünk. A Kleiber-törvény egy szublineáris skálázás, ami log-log ábrázolásban egy ¾-es meredekséget jelent. Az egyszerűség kedvéért a továbbiakban itt úgy hivatkozunk erre, hogy az állatvilágban 0,75-ös skálázás figyelhető meg. Hogy ez a szám miért pont 0,75, azt a bennünk lévő (ér)hálózatok szerkezetéből lehet levezetni.
A város mint ember alkotta szuperorganizmus
Találunk-e a Kleiber-törvényhez hasonló egyszerű összefüggéseket a városokra, azaz az emberek alkotta szuperorganizmusokra? Geoffrey West szerint igen. Például kiderül, hogy egy lakosra nézve egy ötmilliós város mindössze feleannyi benzinkúttal képes fenntartani a közlekedését, mint egy ötvenezres. De szám szerint is hasonló skálázás figyelhető meg az elektromos kábelek és a vízvezetékek hosszában. És a felhasznált energiában is, legalábbis a könyvben felsorolt tudományos publikációk szerint. Ha az egyik várost kétszer annyian lakják, mint a másikat, akkor benzinkútból és elektromos kábelből a kétszereséhez képest 15 százalékkal kevesebb szükséges. Ez a 15 százalékos ugrás „önhasonló” módon figyelhető meg. Mindegy, hogy egy tízezer fős várost hasonlítunk össze egy húszezressel vagy egy egymillióst egy kétmillóssal. A duplázásonkénti 15 százalékos spórolás 0,85-ös szublineáris skálázást jelent az infrastruktúrában.
Az infrastruktúra, és különösen az energiafelhasználás skálázása önmagában is lényeges. A világ leggazdagabb részén a biológiai 100 W helyett egy ember 11 kW-ot használ jelenlegi életvitelének fenntartására, ami a kék bálna biológiai energiaigényének felel meg. Ez összesen annyi energia, mint ha tízezer éve 200 milliárdan lettünk volna. Az évszázad végére ebben az értelemben 1000 milliárd urbánus körülmények között élő embert kell ellátni energiával (és ivóvízzel).
Ugyanakkor egy városról sosem az elektromos kábelek vagy az úthálózat hossza jut először az eszünkbe, hanem az, hogy az infrastruktúra mennyire könnyíti meg a városlakók életét. A város a városlakókat jelenti, nem pedig a kábeleket és a betont. Ezt az átütő felismerést többek között Jane Jacobs aktivistának köszönhetjük, aki az amerikai városokról (leginkább New Yorkról) írt egy klasszikus könyvet a hatvanas években, ami alapjaiban késztette átgondolásra a várostervezést.
Több a mobil, mint a WC
Hogyan lehet számszerűsíteni azt, hogy egy város a városlakókat jelenti? Az elektromos kábelek hosszát le lehet mérni centiméterrel. Hogyan lehet mérni az emberi interakciókat, akik egymással beszélnek, találkoznak, dolgoznak, szórakoznak, és ehhez a városon belül utaznak? Úgy, hogy állandóan mobiltelefont használunk. Egy átlagos amerikai naponta három órát van mobilon, ami közben folyamatosan digitális nyomokat hagy. Mobiltelefonhoz pedig mára többen jutnak hozzá a bolygón, mint WC-hez.
Ez a hatalmas adatmennyiség forradalmasítja a szociológiát. Kiderül, hogy egy félmilliós portugál város átlagos lakója kétszer annyit telefonál, mint egy ötezres településen élő. Miközben azon ismerőseink száma, akik egymással is tartják a kapcsolatot (extended family) nagyjából független a településmérettől, egy nagyobb városban sokkal diverzebb kapcsolatok épülnek ki, és sokkal több időt töltünk olyan emberekkel, akik nem szoros barátaink. Robin Dunbar antropológus nevéhez köthető a 150-es szám, ami azt mondja, hogy az emberek kényelmesen nagyjából 150 közvetlen emberi kapcsolatot tudnak egyszerre fenntartani. Ebből 5 emberrel nagyon szoros kapcsolatot, 15 közelebbi baráttal kicsit kevésbé erőset, másik 50 ismerőssel sokkal lazábbat, a többiekről pedig éppen csak tudunk dolgokat.
Mennyi interakció, azaz kapcsolat létezik egy városban? Ha egy szobában két ember tartózkodik, akkor azok között a kapcsolatok száma 1. Három ember között 3 kapcsolat lehet, négy között 6 kapcsolat, öt között 10, hat között 15... Ha nagyon sok embert tekintünk, akkor az összes lehetséges kapcsolat száma nagyjából az emberek számának négyzetével (pontosabban annak a négyzetének felével) lenne arányos. Ez az állatos példán elmondottak alapján egy 2-es skálázást jelentene, miközben a megfigyelések egy jóval kisebb, 1,15-ös skálázásra utalnak. Ez nem meglepő, hiszen ha mentálisan lenne is kapacitásunk a város összes másik lakójára, fizikailag akkor sem tudnánk folyton találkozni a városban mindenkivel.
A találkozások számát korlátozza, hogy naponta legfeljebb másfél órát szeretünk utazni vagy bolyongani. Ha ennél kevesebb időbe telik eljutni a munkahelyre, akkor a maradék időben vásárolunk, sétálunk. Ha ennél több idő megy el naponta utazással, akkor valószínűleg rövidesen munkahelyet váltunk. Ezt a másfél órát még a rabok is lesétálják a börtönben. A mindenkori utazási sebesség és ez a másfél óra meghatározza a városok karakterisztikus méretét. (Ezért van, hogy pár évszázaddal ezelőtt minden kultúrában és birodalomban hasonló méretű városok jöttek létre. A városmérettel azért megfigyelhető egy sebességnövekedés is, sőt, van ahol külön gyorssávok vannak a gyorsabb gyalogosoknak. A mobilitásban lévő szabályosságokat kutatják például a svájci-szingapúri Future Cites Labnél.)
Kétszer nagyobb város, kétszeresnél nagyobb aktivitás
Miért érdekes ez az 1,15 skála? Azért, mert az általunk felépített világ, a megtermelt vagyon, az egy főre eső GDP vagy mondjuk az éttermek száma mind összefüggésben áll azzal, hogy közösségben élünk. És a könyvben hivatkozott kutatások szerint ezek mind 1,15-tel is skálázódnak. Kétszer akkora városméret a kétszereshez képest 15 százalékkal nagyobb szociális és gazdasági aktivitást jelent, annak a jó és rossz oldalával egyaránt. Az innováció és a bűnözés is szuperlineárisan nő, miközben egy kétszer akkora város 15 százalékot spórol az infrastruktúrán. Az infrastrukturális hálózatok szublineárisan (0,85), a szociogazdasági hálózatok pedig szuperlineárisan (1,15) skálázódnak. Az aktuális számok persze országfüggők: más a bűnözési ráta egy japán városban, mint egy amerikaiban, de a skálázás országtól és kultúrától független.
Ha ez így van, akkor érthető, hogy egy nagyvárosban miért egyre gyorsabb ritmusú az élet a méret növelésével, miközben az állatok esetén pont fordítva van. Az élőlények szívveréseinek száma egy életben meglepően állandó az egértől az emberen át egészen a kék bálnáig, de a méretnövekedéssel egy szívverés hossza lassul. Az élőlények idővel meghalnak, míg a városok évszázadokon át léteznek, háborúkat is átvészelve, és lakosságszámban az exponenciális bővülést meghaladó gyarapodást mutatnak.
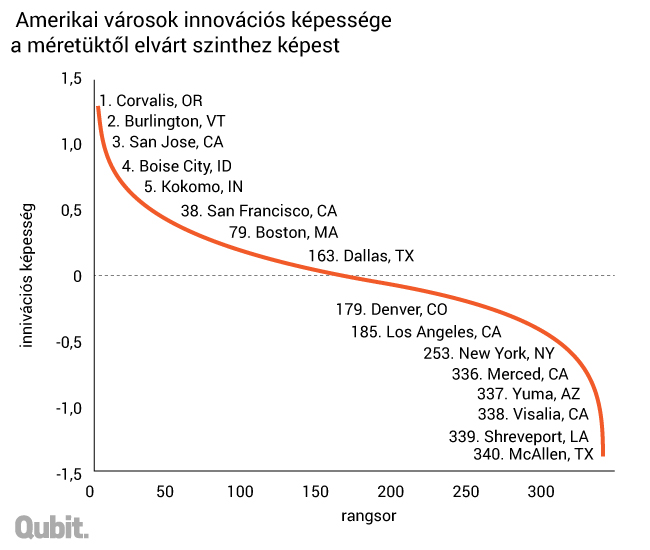
Ha ez így van, akkor át kell gondolni azokat az indexeket, amiket az Economist Intelligence Unittól a Forbeson át különböző intézetek közölnek a városokat egymással összehasonlítva. Egy város gazdaságilag jobban teljesíthet pusztán azért, mert nagyobb. Ha ezeket a méretbeli előnyöket eltávolítjuk, akkor az adatokból kiderül, hogy New York szinte minden tekintetben nagyon átlagos amerikai város. Egy New York-i nem is szegény, nem is gazdag. (New York egy valamiben emelkedik ki: feltűnően biztonságos.) Ennek alapján érdemes inkább megítélni a városvezetés eredményességét, figyelembe véve, hogy egy intézkedés hatása nagyon hosszú távú is lehet. Ebből az analízisből derül ki, hogy a kaliforniai San José már akkor nagyon kiemelkedett a többi város közül, mielőtt a Szilícium-völgy központja lett. Az is kiderül a történelmi adatsorokból, hogy ilyen sikereket nemigen lehet tervezéssel előírni.
Persze akkor, ha mindez így van. A városok tudománya új terület, magyarul is lehet találni róla népszerűsítő előadásokat. Ezen a videón például Bokányi Eszter beszél arról, hogy fizikusok hogyan vizsgálják a városokat. De gyorsan jönnek az új eredmények: amikor a könyv készült, már jelentek meg cikkek arról, hogy vajon tényleg szinte minden olyan egyszerű módon függ-e a város méretétől, hogy a log-log skálán egyeneseket látunk, ugyanazzal az 1,15-ös számmal. Ez a cikk azt vizsgálja, hogy mennyire függ ez az egész attól, hogy miként definiáljuk a városok határait (vannak kétségek). Egy másik cikk, amely angliai és wales-i városokat elemez, ennél is kritikusabb a hatványüggvények illesztésével kapcsolatban. Kiderül, hogy a nemzetközileg beágyazott Londont és a többi várost teljesen külön érdemes kezelni.
Ami még érdekesebb, hogy ennek a második cikknek a végén idéznek négy tanulmányt, amelyek az egy főre eső szén-dioxid-kibocsátást vizsgálják, és ellentmondások találhatók bennük. Nem egyértelmű, hogy a szén-dioxid-kibocsátás hogyan skálázódik a népességszámmal: azzal arányosan (lineárisan) nő, vagy arányosan kevésbé (szublineárisan) vagy azon felül (szuperlineárisan). Ez azért lényeges, mert míg tízezer éve megettük a növényeket és a növényeket megevő állatokat, amely növények fotoszintézissel jutottak hozzá az éppen beérkező napenergiához, mára leginkább a fosszilis energiahordozókban tárolt (nap)energiát használjuk, amihez kémiai égetéssel férünk hozzá. Egy hőtani szempontból nyílt rendszert egyre inkább zárt rendszerré tettünk, és entropikus melléktermékként egyre több szén-dioxiddal fűtjük az atmoszférát.
West könyve precízen leírja, hogy míg a gazdaság egésze exponenciálisan nő, az exponenciálisnál gyorsabb (szuperexponenciális) növekedés elméletileg más. Nagyjából: a sima exponenciális bővülős végtelen idő alatt éri el a végtelent, míg a szuperexponenciális véges idő alatt lesz végtelen. A városok ez utóbbi dinamikát követik.
Fenntartható a növekedés?
Fenntartható-e ez? A növekedéstől való félelem nem új. Thomas Malthus és követői kétszáz éve is attól féltek, hogy a növekvő népességet nem leszünk képesek élelmezni. Nem számoltak azonban az innovációkkal, amik eddig mindig növelni tudták a produktivitást. Egy jelentős innováció tehát átírja a korábbi dinamikát egy gyorsabbra. Ezeknek az átírásoknak ugyanakkor egyre gyakrabban kell megtörténniük. Egész életen át kell tanulni, a figyelmünkért éles harc folyik, ugyanakkor a technológiával elképzelhető lehet a biológiai korlátok valamilyen kitolása. Kiborgokká leszünk, vagy valami olyan jön, amit el sem tudunk képzelni? Ezekről sokat filozofál West könyvének utolsó fejezete, ugyanakkor egy szó sem esik arról, hogy a népességszám egyszer tetőzni fog, ami alapjaiban írhatja át a városok dinamikáját. Nem beszélve az öregedő társadalom kihívásairól, ami Japánban és Európában a valóság, de Kína is szembenéz vele az évszázad közepére.
Szintén kritikusan látom azt, hogy a könyv a Manhattan tervhez hasonló fenntarthatósági projektre híva fel a figyelmet. Inkább több kisebb, egymással versengő műhelyre lenne talán szükség, mert a nagy kutatócsoportok kevésbé lesznek egy idő után eredetiek. Ezekkel együtt mindenképp érdemes a kötetet beszerezni. Tele van tudomány- és technikatörténeti érdekességekkel, például a hajók skálázásáról, lényeges urbanisztikai, szociológiai, hálózattudományi hivatkozásokkal. Sokszor túlságosan csapongó és önmagát ismétlő, viszont cserébe egy-egy fejezet önmagában is teljesen megérthető.
Ui. Köszönöm azoknak a fizikus és közgazdász barátaimnak, akik a megjelenés előtt a cikket elolvasták, és hasznos tanácsaikkal olvashatóbbá tették. Külön szeretném megköszönni Bokányi Eszternek a szakmai lektorálást.
A szerző az Uppsalai Egyetem fizikus kutatója.
Korábbi kapcsolódó cikkek a Qubiten: