A hangyahurok című feladványban egy hangya egy kezdetben vízszintes pálcán iszkol a felfele emelt végponttól a pálca másik vége felé, ami a talajon csúszik. A hangya sebessége a pálcán, valamint a pálca végének emelkedési sebessége azonos, ezért a hangya pont akkor ér a pálca végére, mire az teljesen felegyenesedik. Ezért aztán a hangya végül ugyanoda jut vissza a talajhoz viszonyítva, mint ahonnan elindult. A kérdés az volt, hogy milyen irányba indul a hangya a talajhoz viszonyítva, illetve hogy a megtett huroknak mi a legmagasabb és a legszélsőbb pontja.

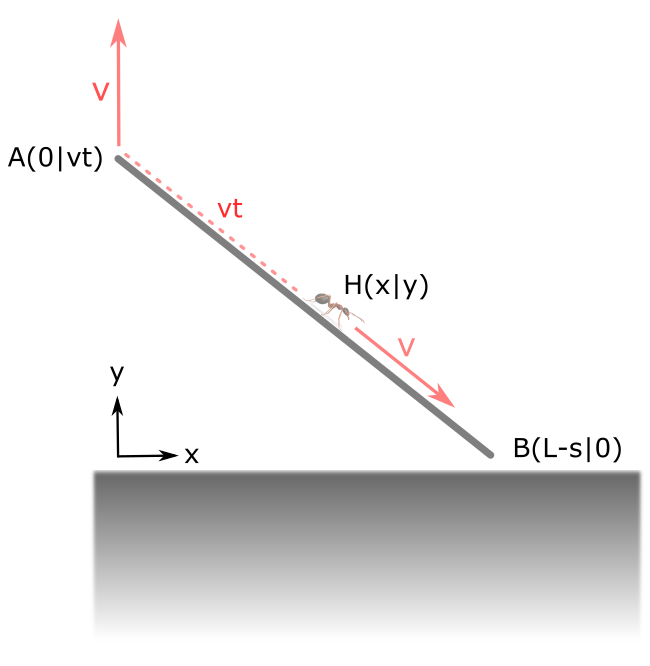
Helyezzük a koordináta-rendszerünk origóját a hangya kezdeti pozíciójába, és jelöljük ezt a pontot O-val. Az L hosszú pálca függőlegesen emelt vége legyen A, a másik vége B. A mozgás elején A = O, a mozgás végén B = O. A pálcán v sebességgel haladó hangya t időpillanatban vett helyzete legyen H, amit x(t) és y(t) koordinátákkal írhatunk le. A t időpontig a hangya v·t utat tesz meg, amit az ábrán piros szaggatott vonalllal jelöltünk. A pálca alsó vége ezalatt s utat tesz meg. A koordináta-rendszerben való leírás a kérdések megválaszolásához nem is feltétlenül szükséges, később azonban az illusztráció kedvéért kirajzoljuk majd a hangya által megtett hurkot, és ennek a görbének a leírása a koordináták segítségével kézenfekvő.

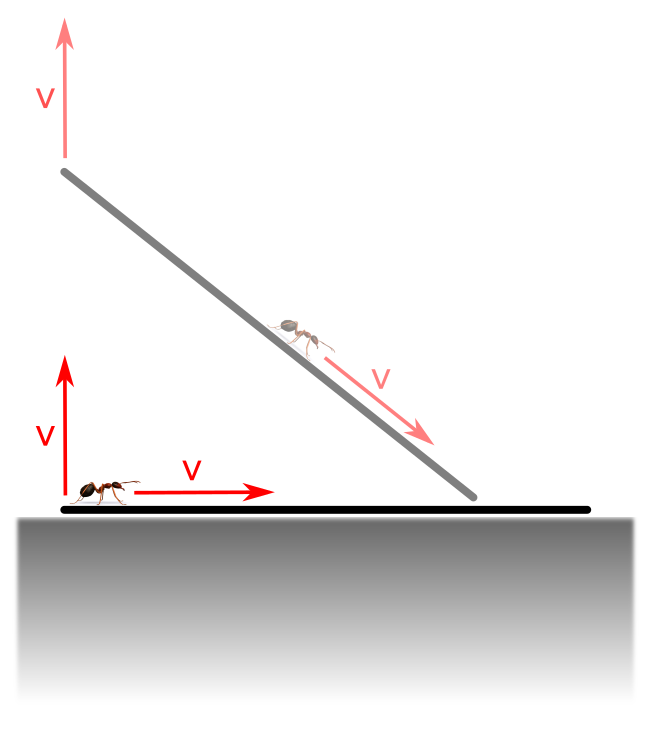
Nézzük az első kérdést, hogy milyen irányba indul a hangya a talajhoz viszonyítva. A hangya talajhoz viszonyított sebessége két összetevőből adódik össze: a pálca sebességéből a talajhoz viszonyítva, valamint a hangya sebességéből a pálcához viszonyítva. Az előbbi esetében a pálca azon pontjának a sebességére vagyunk kíváncsiak, amely pontban a hangya éppen tartózkodik, ami a mozgás legelején az A pont, ami v sebességgel mozog felfele. Ugyanekkora sebességgel mozog a hangya is a pálcán, ami kezdetben vízszintes, tehát az eredő sebesség pont 45 fokot fog bezárni a vízszintessel.

Most nézzük, milyen magasra jut a hangya. A hangya sebessége a mozgás során végig két összetevőből áll össze, ahogyan azt fentebb megállapítottuk, de most elegendő ezeknek csak a függőleges komponenseit tekintenünk. A hangya függőleges irányú sebességét kezdetben a pálca mozgásából adódó komponens fogja dominálni, és a hangya egyre magasabbra fog jutni. Tudjuk azonban, hogy a mozgás végén visszatér O-ba, tehát később megfordul a mozgása. Legmagasabban akkor lesz, vagyis akkor fordul vissza, amikor az eredő sebességének a függőleges irányú komponense éppen nulla.

Mivel a rúd A végpontjának a függőleges irányú sebessége v, a B végpont viszont a talajon marad, tehát nincsen függőleges irányú sebessége, ezért a hangya a rúdon elfoglalt helyével arányosan veszi át a rúd A végének a sebességét, így az v · (HB/AB) lesz. Azt a jelölést követjük itt és a továbbiakban, hogy tetszőleges P és Q pontok esetén PQ a két pont által meghatározott szakasz hosszát jelenti. A hangya saját sebessége a rúdhoz viszonyítva v, aminek a függőleges komponense v · (OA/AB), csak ellenkező irányban. A hangya eredő függőleges sebessége akkor lesz nulla, ha a fenti két komponens nagysága azonos, ami HB = OA esetben áll elő. Viszont OA = AH = v·t, tehát ebben az esetben HB = AH, vagyis a hangya pont a rúd közepén van, a hangya által elért magasság pedig OH = OA/2 = AB/4 = 5 cm. Továbbá még azt is megállapíthatjuk, hogy a rúd éppen 30 fokos szöget zár be a vízszintessel.

Ha az a kérdés, hogy x irányba milyen messze jut a hangya, akkor hasonló módon a korábbiakhoz, most azt keressük, hogy a hangya eredő sebességének vízszintes komponense mikor válik nullává. Legyen a rúd B végének a vízszintes sebessége u, ami függhet az időtől. A rúdtól kapott vízszintes irányú sebességet a hangya a rúdon elfoglalt helyének megfelelően most is arányosan veszi át, mert az A pont nem mozog vízszintesen. Az u nagyságú sebességéből a hangya u · (AH/AB) sebességet vesz át. Saját rúdon levő sebességének vízszintes komponense pedig v · (OB/AB). A vízszintes irányú visszafordulás tehát akkor történik, amikor u/v = OB/AH = OB/OA = 1/tg(α), ahol α a rúdnak a vízszintessel bezárt szöge.

Most használjuk ki azt, hogy a rúd merev, nem nyomódik össze, ezért mindkét vége egyforma sebességgel kell mozogjon a rúd saját irányába, vagyis a rúdvégek sebességeinek vetülete a rúdra egyforma kell legyen. Ebből az következik, hogy u·cos(α) = v·sin(α), vagyis  u/v = tg(α). Tehát tg(α) = 1/tg(α), ami α=45°-nál teljesül, vagyis a derékszögű AOB háromszög egyenlő szárú, tehát AH = OH = L/√2. AH-t levetítve az x tengelyre kapjuk, hogy a hangya eltávolodásának maximuma AH · cos(α) = L/2 = 10 cm.

A megoldást Miholcs Gyula marosvásárhelyi beküldőnk megoldása alapján állítottam össze.

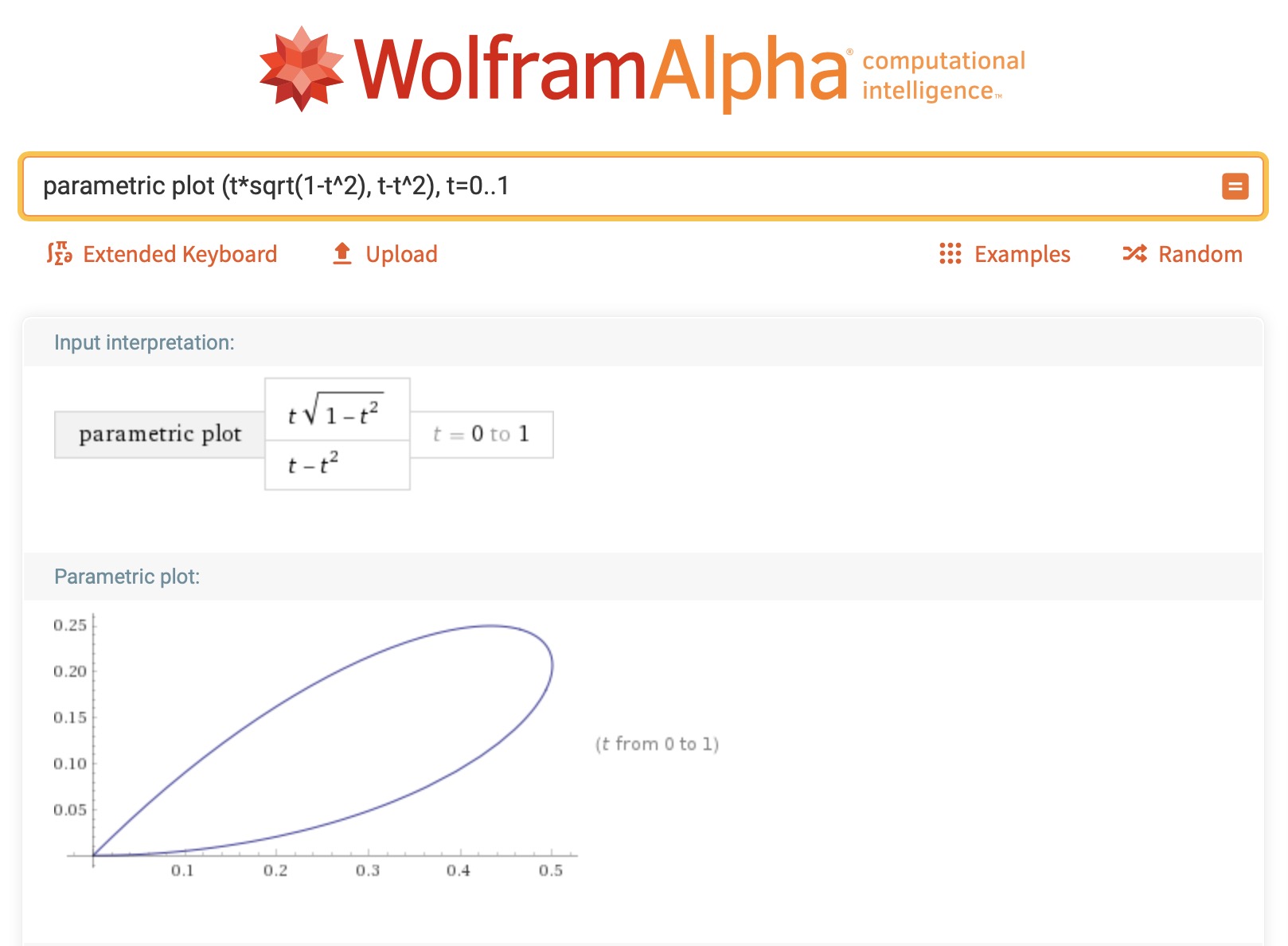
Érdekességként nézzük még meg, hogyan is néz ki ez a hangyahurok teljes valójában. Ha L-et és v-t egységnyinek választjuk, akkor a görbe paraméteres egyenlete, azaz x és y koordinátái az idő függvényében: x(t) = t · sqrt(1-t^2), y(t) = t-t^2. A kirajzolásban segítséget nyújthat a WolfraAlpha online felülete, csak azt kell neki beírni, ami az alábbi képernyőképen is látszik a narancssárga keretben.