A járványdinamika segít abban, hogy megértsük, miről szólnak a mostani intézkedések
A járványdinamikában alkalmazott úgynevezett SIR modell alapfeltevése, hogy van egy fogékony populáció, amiben a kórokozó szabadon terjedhet. A SARS-CoV-2-re az emberiség fogékony, így ez teljesül. Az ökológia és az evolúcióbiológia egyik alaptörvénye, hogy a populációk exponenciális növekedésre képesek, és ezt a növekedést mutatják, amikor a forrásaik nem korlátozzák növekedésüket. A fertőzés kezdetben egyértelműen exponenciálisan növekszik.
Az exponenciális növekedés sokkal gyorsabb a lineárisnál
Egyenes arányosságban sokkal otthonosabban mozgunk, mint az exponenciális növekedés világában. Sajnos olyankor is hajlamosak vagyunk lineáris növekedésre gondolni, amikor nem erről van szó. Ott van a matematikában ismert búzaszem- és sakktáblaprobléma, amelyben Ibn Kallikan vagy Sessa ebn Daher (a történetnek több verziója ismert) azt kéri, hogy a sakktábla minden mezőjére kétszer annyi búzaszem kerüljön, mint az előzőre. Ez úgy kezdődik, hogy 1, 2, 4, 8, 16, stb. A még apró számok csábíthatnak, hogy gondolatban úgy folytassuk 28, 36, 44 stb. és érjünk el 488-ig a 64-ik mezőn. Ennyi búzaszemet minden valamirevaló uralkodó tud adni kedves tudósának. De búzás sorozat mértani (a két egymást követő érték hányadosa állandó) és nem számtani (a két egymást követő érték különbsége állandó). A 64. mezőre rakandó búzamennyiség (263) sokkal több, mint amennyit eddig összesen előállítottunk búzából.
Ami a koronavírus terjedését illeti, vegyük észre, hogy gondolhatjuk, hogy ha ma bejelentenek három új fertőzöttet, meg holnap is hármat, meg utána is hármat (és így tovább), akkor egy hónap alatt 90 új fertőzött lesz. Ez egy kezelhető szám. A folyamat kezdeti leírására viszont inkább a következő egyenletet kéne használni:
It+1=λIt
A fertőzött populáció (N) minden időintervallumban a λ-szorosára nő – ez utóbbit bruttó növekedési rátának nevezzük. Amennyiben az időintervallumot a fertőzőképesség átlagos idejének vesszük, akkor λ helyettesíthető a sokat emlegetett R0-lal (alap reprodukciós szám), tehát azzal, hogy a fertőzőképesség alatt hány másik embert fertőz meg valaki (erre még visszatérünk).
A fertőzés valószínűségének csökkentésével tartható kordában a járvány
A járványdinamika alapmodellje a SIR, amely mozikaszóban az S a fogékonyakat (susceptible), az I a fertőzötteket (infected), míg az R a gyógyultakat (recovered) jelöli. Az egész népességet (N egyed) ezen három kategóriára osztjuk. Kezdetben majdnem mindenki fogékony, van pár fertőzött, és nincs még gyógyult. A fertőzés bizonyos rátával (β) véletlen találkozások útján történik fertőzött és fogékony személyek között. A fertőzésből pedig egy másik rátával kigyógyulnak (γ) az emberek. A gyógyultak nem fertőzhetők újra, mert immunissá váltak a betegségre. Az 1/γ hányados megmutatja, hogy átlagosan mennyi ideig fertőzőképes valaki (vagy mennyi idő kell a kigyógyuláshoz). Az 1/β pedig, hogy hány másik embert fertőz meg egységnyi idő alatt, így az alap reprodukciós érték, az R0, a β/γ hányados.
Ezen nagyon egyszerű modell egy kimenetelét nézzük most meg. Induljunk ki egy teljesen fogékony populációból, amibe kevés fertőzöttet rakunk. A R0 értéket most állítsuk be 5-re (az nagyon magas) és az 1/γ legyen 5, ami átlagosan öt napos kigyógyulást jelent. Azt látjuk, hogy a fertőzöttek száma meredeken emelkedik, elér egy csúcsot, majd csökkeni kezd, míg mindenki fel nem gyógyul.
A fertőzés azért fullad ki, mert már nincs kit megfertőzni, és a fertőzöttek egyre inkább már csak gyógyult és így a fertőzésre immunis egyedekkel találkoznak. Ez azt jelenti, hogy az effektív reprodukciós szám (azaz, hogy átlagosan hány személyt tud megfertőzni egy fertőzött, RE) folyamatosan csökken, míg 1 alá nem ér, amelytől kezdve a járvány kifullad. Az R0 jelölésben a 0 pont arra utal, hogy az a kezdeti időben érvényes, amikor még lényegében mindenki fertőzhető és a fertőzött csak fertőzhetőkkel találkozik, akiknek átadhatja a kórt. Egy olyan kórokozó, amelynek az R0 értéke már eleve 1-nél kevesebb, nem is okoz járványt.
Az effektív reprodukciós szám kétféleképpen vihető 1 alá: vagy a gyógyulás gyorsabb (γ magasabb) vagy kevesebb másik embert fertőz meg egy fertőzött (β alacsonyabb). A gyógyulás sebességét lehetne elvileg gyógyszerekkel segíteni, de jelen járványnál ilyen nem áll rendelkezésre. A másik lehetőség az új fertőzések megakadályozása. Ez működhet!
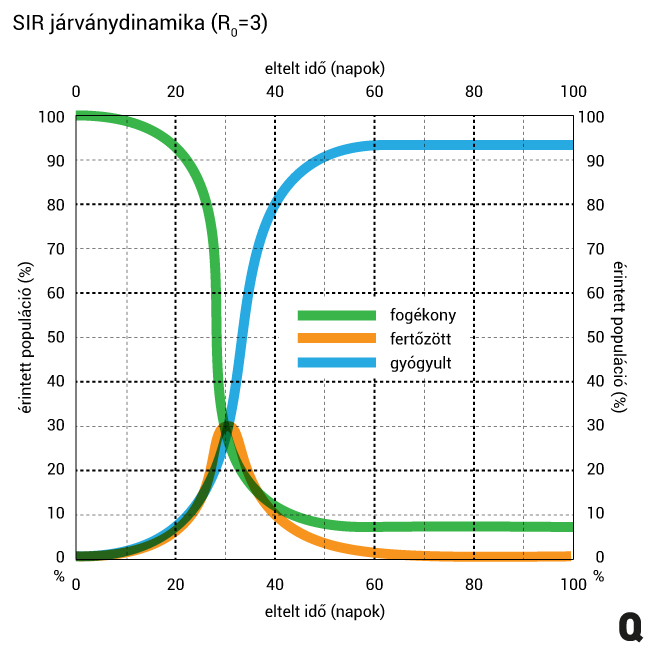
Nézzük meg az elképzelt járvány dinamikáját alacsonyabb, R0 = 3-as értéknél. Két dolgot figyeljünk meg! Az egyik, hogy a fertőzés csúcsa, azaz, hogy egyszerre hányad része beteg a populációnak, alacsonyabb. A másik, hogy nem mindenki fertőződött meg, maradtak fogékonyak a populációban, miközben a járvány kifulladt.
Az egészségügyi rendszert nem az összes fertőzött, hanem az egyszerre jelen levő fertőzöttek száma terheli túl
A médiában most sokat beszélnek a „flatten the curve” azaz a görbe ellaposítása jelenségről. Egy lassabban terjedő járvány esetén az egyszerre betegek száma alacsonyabb. Először is tekintsünk vissza az első ábrára, amelyen lényegében mindenki megfertőződik. Ennek ellenére nem igaz, hogy egyszerre mindenki beteg. A betegségeknek és a fertőzésnek is van egy lefolyása. Az elején kevés fertőzött még kevés más embert tud megfertőzni, és eltelik egy idő, amíg az egyre több fertőzött egyre több fertőzhetőt ér el. De addigra már az első betegek meg is gyógyulnak. A magas fertőzőképességű esetben is egyszerre olyan 50 százaléka beteg, a járvány lefolyása viszont gyors.
A két járvány lefutásának összehasonlításából látszik, hogy a járvány tetőzésekor lényegeseb kevesebb beteg van. Vegyük ehhez még az alábbi R0=2-vel számolt lefolyást, és egyértelműen látszik, hogy a fertőzés sebességének csökkentésével egyre kevesebben betegek egyszerre.
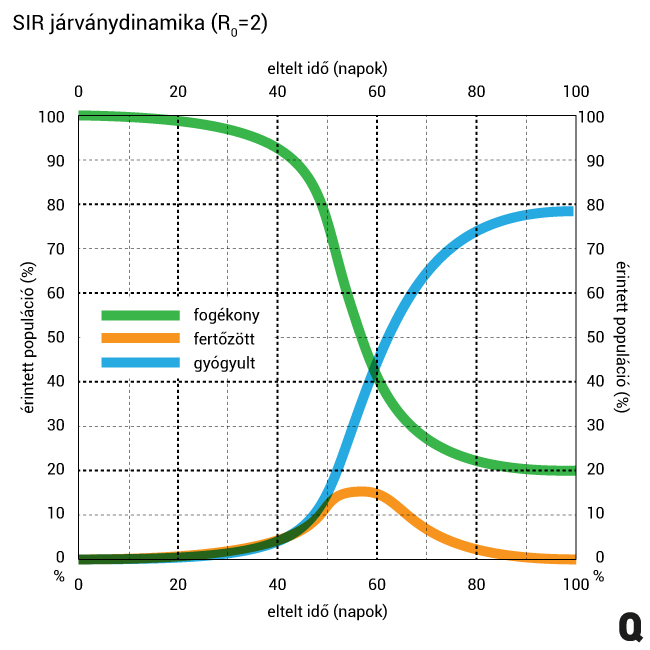
Az egészségügy kapacitása véges. Egyetlen országban sem számolnak olyasmivel, hogy ilyen tömegben van szükség egyfajta kórházi kezelésre. Minél kisebb az egyszerre jelentkező esetszám, annál kevésbé van leterhelve az egészségügy. A jelenlegi intézkedések ezt az időbeli elhúzást kívánják elérni, amivel a járvány időtartamát kitolják ugyan, de az egészségügy leterheltségét csökkentik.
Lassabb terjedés mellett kevesebb ember fertőződik meg
Az előző három ábrát nézve még valami feltűnhet: járvány végén a fogékonyak száma R0 csökkenésével egyre nő. Azaz egyre több olyan egyed van, aki nem is fertőződött meg! Ez is egy hozadéka a terjedés lassításának. Megmutatható, hogy az így érintetlenül maradók a populáció e-R0R részét teszik ki (R a meggyógyultak végső aránya; Miller 2012). A fenti példákban rendre a populáció 0,7, 5,9 és 20,31 százaléka nem betegszik meg.
Megjegyzés az R0 értelmezéséről
Az R0 értékkel kapcsolatban van egy tévhit, miszerint azt jelenti, hogy egy fertőzött hány embernek adja tovább a fertőzést, kihagyva az „átlagosan” kitételt. Azaz, ha valaki R0=3 mellett megfertőzött három másik személyt, akkor már nem fog többet. Ez egy átlag. Lesz, aki senkit nem fertőz meg, és lesz, aki sokakat.
Az átlagos R0 bár mond valamit a terjedés sebességéről, jelentős heterogenitást fed el. A járványt tömegjelenségként értelmezve minden személyt hasonlónak veszünk. Tudjuk azonban, hogy mind a vírusszámban, mind az egyéni életvitelben különbség lehet az emberek között, ami változtatja a fertőzőképességet. Loyd-Smith és munkatársai (2005) még a SARS járvány kapcsán mutatták meg, hogy minél nagyobb a variancia a megfertőzödöttek számában, annál nagyobb az esélye a járvány kihalásának, de egyben egy jelentős fertőzésszám-robbanásnak is. Ez is állhat amögött, hogy különböző országokban más a járvány kezdeti dinamikája. Egyre összetettebb modellekben figyelembe tudják ezt venni, de az alapvető jelenségek szemléltetésére a lehető legegyszerűbb modellt érdemes használni.
Ez az egyszerű modell nem írja le a COVID-19 járványt
A SIR modell alapfeltevése, hogy igen nagy és jól kevert populációban terjed a járvány, és a fertőzöttek azonnal fertőzőképesek. A járvány kezdeti szakaszában a populáció jól kevertsége igaz is lehet, főleg az olyan nagyvárosokban, mint Vuhan vagy Budapest. Viszont tudjuk, hogy nem minden korosztály azonosan keveredik (ez a fiataloknál jelentősebb mértékű). Továbbá van lappangási idő, amelyben még nem fertőzőképesek a fertőzöttek. Ezek és több más paraméter is figyelembe vehető, amennyiben egy konkrét járványt, például a COVID-19-et szeretnék modellezni. Ezen lehetőségekről és a COVID-19-cel kapcsolatos modellezésekről egy újabb bejegyzésben írok.
A szerző az MTA - ELTE Elméleti Biológiai és Evolúciós Ökológiai Kutatócsoport főmunkatársa. További cikkei itt olvashatók.
Hivatkozott irodalom
Lloyd-Smith, J. O., Schreiber, S. J., Kopp, P. E. és Getz, W. M. 2005. Superspreading and the effect of individual variation on disease emergence. Nature 438(7066): 355–359
Miller, J. C. 2012. A note on the derivation of epidemic final sizes. Bulletin of Mathematical Biology 74(9): 2125–2141
Kapcsolódó cikkek a Qubiten: