Hét matematikus és a pizza című feladványunkban az volt a kérdés, hogy legkevesebb hány egyenes vágással szelhető fel egy kör alakú pizza úgy – közben nem elmozdítva a darabokat –, hogy a végén mind a heten ki tudnak venni maguknak egy-egy azonos területű (akár több darabból álló) részt, és lesz egyvalaki, aki egyáltalán nem kap a pizza széléből.

Egy vágással a pizza két részre vágható. Egy következő vágással a két korábbi rész mindegyike elvágható még két részre, tehát két egyenes szeléssel maximum négy részre tudjuk vágni a pizzát. Gondolhatnánk, hogy egy harmadik vágással, ami átmegy a korábbi szeletek mindegyikén, ez tovább duplázható, de sajnos nincs olyan egyenes, ami átmegy a korábbi darabok mindegyikén. Ahhoz ugyanis, hogy a szemközti A és C darabokat kettészelje egy egyenes, a szelő húr végpontjainak az A és C darabokat határoló kék köríveken kéne lenniük (a végpontokat leszámítva), míg ahhoz, hogy a B és D darabokat is kettévágjuk, a szelő húr húr végpontjainak a B és D darabokat határoló piros köríveken kellene lenniük (a végpontokat leszámítva), ami egyszerre nem teljesülhet.

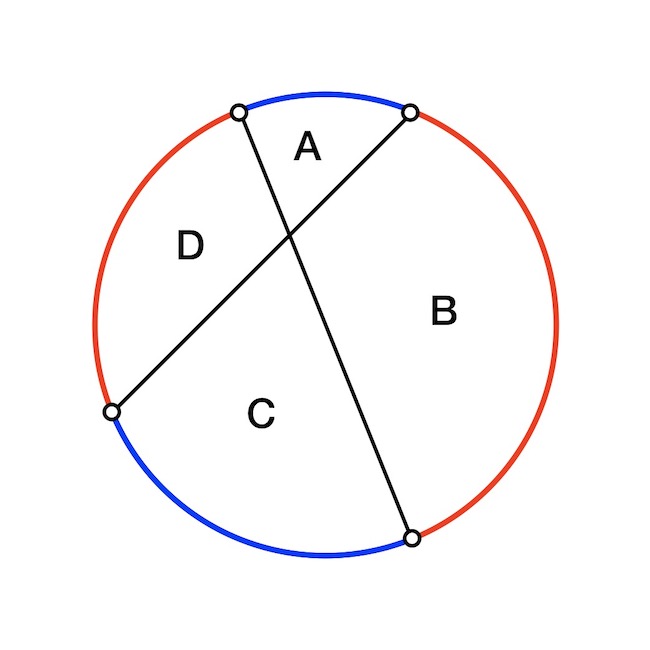
Ha nyolc részre nem vághatjuk három egyenessel a körlapot, akkor maximum hét jöhet szóba, és ez lehetséges is, lásd az alábbi ábrát. Viszont nem lehetséges úgy, hogy a hét rész mindegyikének ugyanakkora legyen a területe (szürke tartományok).

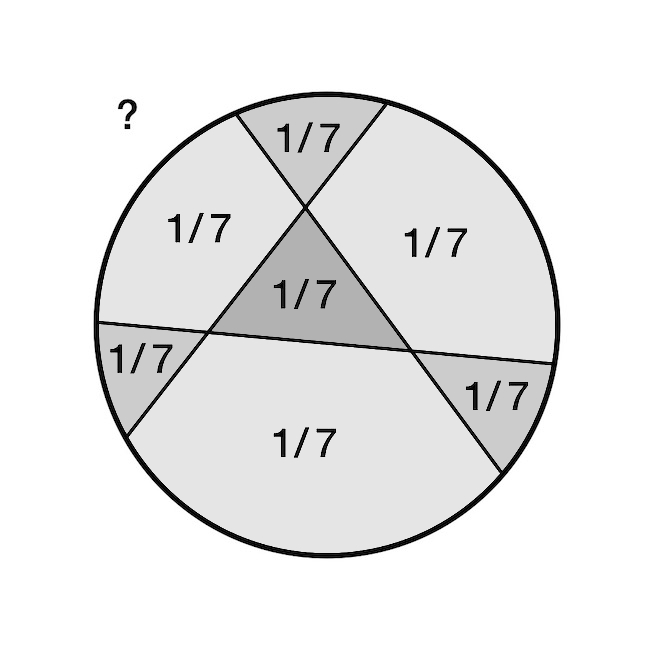
Ha ez lehetséges lenne, akkor a szelők mindegyikének 3:4 arányban kellene osztania a kört, vagyis a szelő egyenesekhez tartozó körhúrok hosszának ugyanakkorának kellene lennie, és kiszámolható, hogy ugyanakkora r ≈ 0,1124·R távolságban kellene elhaladniuk a pizza középpontjától, ahol R a pizza sugara. Az alábbi rajzon berajzoltunk a pizzával koncentrikusan egy ilyen r sugarú kis kört (piros). A használt szelőknek tehát ezt a kört érinteniük kell, a kérdés csak az, hogy a három szelőt egymáshoz képest mennyivel kell elforgatni.

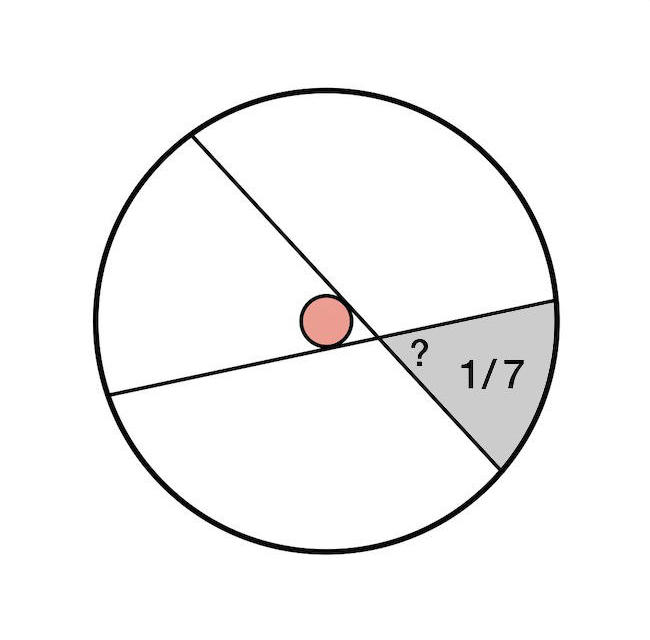
Ha berajzolunk egy ilyen szelőt, majd egy másikat ugyanabból a kezdő pozícióból indítva elkezdünk elforgatni a piros kör körül úgy, hogy azt mindvégig érintse, akkor a két szelő által közrefogott szürke metszet területe monoton fog változni. Egyetlen olyan elforgatási szög lesz, ahol a szürke terület éppen hetede lesz a pizza területének. Ez a szög azonban a meg kéne egyezzen a második ábrán látható sötétszürke belső háromszög összes szögével, tehát annak egy szabályos háromszögnek kellene lennie 60 fokos szögekkel. Ha azonban kiszámoljuk 60 fokos metszési szög esetén a szelők által közrefogott szürke területet, akkor az nem a nagy kör területének hetede lesz.

Azt kaptuk tehát, hogy legalább négy vágás szükséges. Négy vágással pedig többféle módon is megoldható a probléma – egy lehetséges megoldást mutat Boros Péter megoldónk alábbi illusztrációja. Itt az alsó vízszintes vágás 3:4 arányban osztja a kört. A két ferde vágás 2:5 arányban, és az elsőhöz képest olyan szögben állnak, hogy a 2/7-es és 3/7-es körszeletek metszete pont 1/7 legyen. A felső vízszintes vágás ezután két egyenlő területű részre osztja a megmaradt 2/7 méretű darabot. Ennek nem is szükséges az első vágással párhuzamosnak lennie.

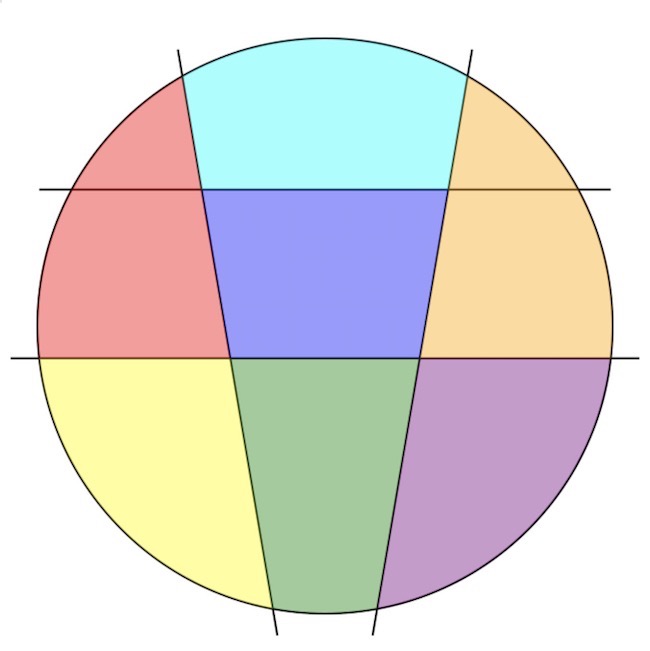
Kapcsolódó cikk a Qubiten: