Az arányok világában élünk. Ha minden egy ütemben változik, akkor nem változik meg semmi; ha a másodperc együtt változik a szívdobogással, akkor nem vesszük észre, hogy gyorsabban dobog a szívünk; ha velünk együtt rövidül a méter hossza, nem vesszük észre, hogy kisebbek lettünk; ha együtt nő velünk az egy kilogramm súlya, nem vesszük észre hogy nehezebbek lettünk; ha megszorozzuk a számlálót és a nevezőt ugyanavval a számmal, a tört értéke nem változik.

A látszat és valóság kötéltánca

A látszat és a valóság kapcsolatának feltárása állandó kötéltáncot jelent: olykor a látszat csap be minket, és változást látunk ott, ahol semmi sem változik, máskor viszont a látszat fedi el előlünk a valódi változást. Ez különösen így van a relativitás elméletében. Korábban az ikerparadoxon kapcsán vizsgáltuk meg, hogyan mehet át a látszat valóságba, ha két inerciarendszert összekötünk. Máshelyütt az állandóság és a pillanat – azaz az energia és erők – viszonya alapján jutottunk arra a konklúzióra, hogy amíg a relativitás speciális elmélete csak a tér és idő látszólagos egymásba fordulását írja le, addig a kölcsönhatás – nevezetesen a gravitáció – által egybekovácsolt rendszerekben a téridő struktúraváltozása már valóságos folyamat. Ebben az írásban arra teszünk kísérletet, hogy felfedjük, mikor rejti el a látszatok világa a valóságos változásokat.

Inerciarendszerek összehasonlítása

Egy hajó siklik a vízen, és a fedélzeten valaki eldob egy követ. A kő pályáját és sebességét viszonyíthatjuk a hajóhoz, de megtehetjük a parton álló ember vagy a vonat utasa szemszögéből is, aki a robogó vonat ablakából figyeli az eseményeket. A három különböző nézőpontból más és más lesz a kő sebessége, és más lesz a hozzá tartozó kinetikus energia. Ezek viszonyát jól leírják a sebesség vektoriális összeadási szabályai, de megváltoznak a szabályok, ha a nagy sebességek tartományába érünk, amelyek már összevethetők a fény sebességével. Ezeket a törvényeket a relativitáselmélet fogalmazza meg, építve az inerciarendszerek fogalmára. Igazi inerciarendszer, amely tökéletesen egyenes vonalú és egyenletes sebességű mozgást végezne, valójában nem létezik, de ez a fogalom mégis jó szolgálatot tesz, ha a sebesség változása, a gyorsulás, kicsinynek tekinthető.

A tér, idő és energia változása az eltérő inerciarendszerekben

A korábbi írás arra fókuszált, hogyan változik meg a kinetikus energia nagy sebességeknél, itt most a potenciális energiából származtatható erőkre kerül sor, hiszen az inerciarendszer választása visszahat a téridő szerkezetére, és emiatt a mozgásokat beindító erőkre is. Amikor egymáshoz képest v sebességgel mozgó két inerciarendszert összehasonlítunk, kulcsszerepet játszik a γ tényező:

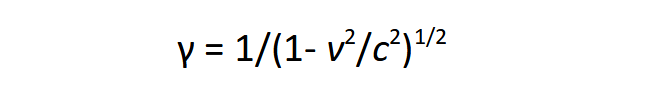
Az elhajított kő helyett most gondoljunk egy űrhajóra, amely fel van szerelve műszerekkel, amivel helyben vizsgálhatjuk a fizika törvényeit. Milyenek lesznek ezek a törvények? Eltérnek-e a földi laboratóriumban megállapított törvényektől? Az inerciarendszerek ekvivalenciaelve azt mondja ki, hogy nincs kitüntetett inerciarendszer, bármelyiket is választjuk, a törvények azonosak lesznek, azaz γ értéke tetszőleges lehet egytől a végtelenig, és így válik relatívvá az idő, a távolság és a tömeg.

A γ tényező határozza meg, hogyan transzformálódnak a tér és idő koordináták, és ez mondja meg a Lorentz-kontrakció és az idődilatáció mértékét is:

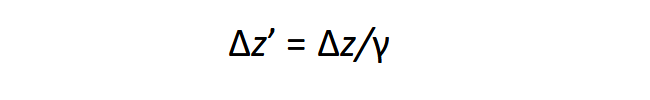
Itt z jelöli ki a mozgás irányát. Hasonló a függés az idődilatációnál is. Fontos megkülönböztetni az időegység (másodperc) növekedését a lassabb órával mért időtartamtól: minél lassabb az óra, azaz hosszabb a másodperc, annál rövidebb időt mutat az óránk, ha mérjük valamilyen esemény lefutását a v sebességű rendszerben:

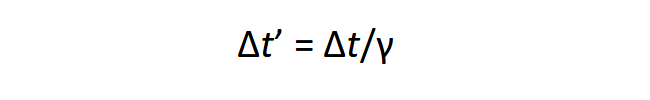
A látszólagos távolság és idő egyformán rövidül, ezért arányuk, a sebesség, azonos marad. Ez biztosítja, hogy a fénysebesség a különböző inerciarendszerekben ugyanaz lesz. A gyorsulás viszont a rövidebb Δt’ miatt γ mértékében növekedni fog.

Ugyancsak γ segítségével adhatjuk meg, hogyan növekszik meg a rendszer kinetikus energiája az E₀ = m₀c² nyugalmi energiához viszonyítva:

A tömeg és energia E = mc² ekvivalenciája, valamint a fénysebesség állandósága miatt megnövekszik a nyugalmi tömeg is:

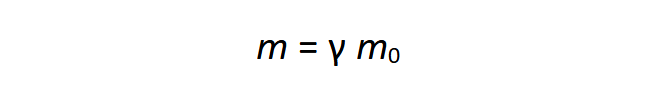
A (4) és (5) egyenlet voltaképp a kovariancia törvény átfogalmazása, amely felváltja a kinetikus energia E_Kin = ½mv² = p²/2m képletét a relativitáselméletben:

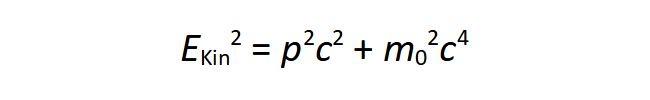
A kinetikus energiához hasonlóan a V potenciális energia is arányosan növekszik γ-val a v sebességű rendszerben, bármilyen kölcsönhatásról is legyen szó:

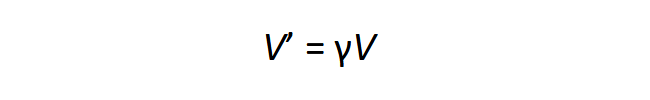
Ebből az elvből következik: ha minden egyformán változik, akkor nem változik meg semmi! A kölcsönhatási erőt a potenciális energia térkoordináták szerinti deriváltja, a gradiens adja meg, amely emiatt γ négyzetével arányosan változik:

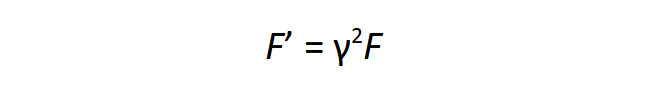
Ez már az F = m·a Newton egyenletből is következik, hiszen mind a gyorsulás, mind a tömeg arányos γ-val.

Elképzelt és valódi változások viszonya

A γ paraméter egy általános rendszerösszehasonlító tényező, amely nem figyelhető meg, míg egyetlen inerciarendszerre korlátozódunk, viszont fontos szerepet játszik, amikor két különböző rendszert összehasonlítunk össze azáltal, hogy az egyik rendszer üzenetét a másikban értékeljük ki. Amíg csak elképzelünk egy másik inerciarendszert – például egy elképzelt űrhajót – addig benne a γ által számított fizikai mennyiségek értéke is csak elképzelt: nem valódi, hanem számításaink műterméke. De megváltozik a helyzet, ha tényleges munkavégzéssel, energiabefektetéssel indítjuk útjára az űrhajót, vagy kezdi el száguldását a sztratoszféra egyik atomjából a kozmikus sugárzás által kilőtt müon. (A müonok bomlási ideje 2,2μs, mégis megfigyelhetők a Föld felszínén, pedig 50 μs alatt érkeznek meg). Az E – E₀ energiakülönbség ekkor már nem az önkényesen kiválasztott inerciarendszerre vonatkozó sebességhez igazodik, hanem a befektetett munka, azaz egy valódi fizikai mennyiség áll az inerciarendszerek szétválasztása mögött. Ez az az energia, ami a gyorsítórakétáktól vagy a sugárhajtású hajtóművektől származik, vagy az, amit a kozmikus sugárzás ad át a müonnak. Ezáltal létrehozunk egy körfolyamatot, amely a szétválással indul, majd a visszatéréssel, illetve valamilyen megfigyeléssel zárul a két rendszer között. A leválasztott rendszer belső folyamatai – például a müon bomlása, az atomóra járása vagy az űrhajós öregedése – már más ütemben történik, mint a földi körülmények között képződő részecskéké, a földi óráké vagy embereké. Mivel az energia minden komponense egy ütemben és arányosan változik, így rejtve marad előttünk, hogy a változás valódi-e, vagy sem. Ennek megállapításához már ki kell lépni saját inerciarendszerből, és kapcsolatot kell keresni a külvilág felé. Ez az a pont, ahol számos eszmefuttatás elbukik, és itt jönnek létre a relativitáselméletet a józan észre való hivatkozás alapján megváltoztatni próbáló elképzelések.

Hogyan változnak meg a fizikai kölcsönhatások különböző sebességű inerciarendszerekben?

Négy alapvető kölcsönhatási formát ismerünk: a gravitációt, az elektromágnesest és a nukleonokban ható erős, valamint a részecskéket egymásba alakító gyenge kölcsönhatást. A potenciális energiát mindegyik kölcsönhatásnál a a tér és idő négy koordinátájában adhatjuk meg, és a transzformáció is azonosan változtat meg minden erőt. Ezt fejezi ki a a V potenciális energia növekedését leíró fenti összefüggés, és ez rejti el a tényleges változást is, amíg nem kapcsoljuk össze az inerciarendszereket valamilyen kölcsönhatással.

Az atomórák működése

Felhasználhatjuk az egyes erőket arra is, hogy méréseket végezzünk. Vegyük például az idő mérését. A jelenleg legpontosabb mérést atomórával érhetjük el, amelyben a cézium-133 atom alapállapotában az első gerjesztett hiperfinom átmenet frekvenciáját veszik alapul. Ez a sugárzás egy másodperc alatt 9 192 631 770 ciklust hajt végre. Erre alapozza a modern tudomány a másodperc definícióját, amit úgy állítottak be, hogy megfeleljen a Föld közepes forgási idejéhez igazított (efemer) másodperc értékének (a földi napok hossza kis mértékben változik). Ez a szabály nulla Kelvin hőmérsékleten érvényes, mivel a hőmérséklet is befolyásolja a frekvenciát.

Nézzük meg a potenciális energia γ-val arányos növekedését leíró általános törvény hatását néhány konkrét kölcsönhatás esetén. Induljunk ki az atomóra esetéből. A hiperfinom kölcsönhatás az elektron és az atommag mágneses nyomatéka közötti kölcsönhatás. Itt a magyarázathoz szükségünk van egy kvantummechanikai kitekintésre is.

Néhány szó kvantummechanikáról

A nem relativisztikus kvantummechanika a Schrödinger-egyenleten alapul, amely a klasszikus p²/2m kinetikus energiát írja át operátorokkal, szemben a Dirac-féle relativisztikus elmélettel, amely ezt a fent leírt kovariancia kifejezéssel teszi meg. A Dirac-egyenlet kibontása a kinetikus energia négyzetgyökvonásán alapul, amely behoz egy kétértékűséget a formalizmusba. Ez vezet el az elektronspin definíciójához, amely új tagokat ad hozzá az energiához, nevezetesen a spin-pálya kölcsönhatást, valamint az elektron és az atommag mágneses momentumai közötti csatolást. Az eredeti Schrödinger-egyenlethez képest mindkét új kölcsönhatás felbontja az energiaállapotokat: az előbbi a finomfelhasadás, az utóbbi a hiperfinom felhasadás elnevezést kapta a spektroszkópiában. A szokásos számítási gyakorlatban a kiegészített Schrödinger-egyenletet használják, amiben szerepelnek a Dirac- egyenletből átvett tagok is. Ez a gyakorlat azonban nem veszi figyelembe a tömeg relativisztikus növekedését, ami legfeljebb mint korrekció szerepel a számításokban. Ennek nagysága az elektronok átlagos sebessége miatt 1 százalék körül van, ami a Coulomb energia és a nyugalmi energia arányából adódik. Számunkra az alapkérdés, hogyan változik meg az elektronpályák energiája, ha a nagy sebességű űrhajó atomjait vizsgáljuk, és ezt a földi körülmények között sugárzó atomokkal hasonlítjuk össze. Ez nem tévesztendő össze azzal a kérdéssel, hogy maguk az elektronok mekkora sebességgel mozognak az atommag körül. Az atommaghoz kötött rendszerben számított energiaszintek az me⁴/ħ² kifejezéssel arányosak, viszont ha mozgó rendszerben vagyunk, ott a tömeg függ az inerciarendszer választásától, mégpedig arányosan γ-val, ami megfelel a potenciális energia növekedését leíró egyenlet követelményének. Ez azt jelenti, hogy az atomok és molekulák által kisugárzott vagy elnyelt fény frekvenciája arányosan növekszik a γ tényezővel.

De hogyan változik az atomórát kalibráló hiperfinom átmenet frekvenciája? A mágneses dipólusok közötti energiát megadó kifejezés:

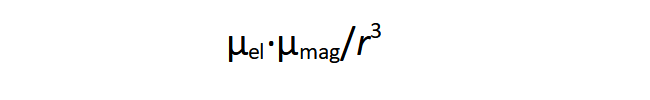
Itt az elektron mágneses momentuma a Bohr-magnetonnal: eħ/2m_elc, a magé a mag-magnetonnal: eħ/2m_magc-vel arányos. A nevezőben lévő két tömeg miatt a kölcsönhatás 1/γ² szerint csökkenne az űrhajó cézium-133 atomjaiban. Ezt kompenzálja azonban, hogy az elektronok eloszlása r csökkenése miatt tömörebb lesz, és az atommagokban γ³-al arányosan megnövekszik az elektronsűrűség. Összességében így a hiperfinom kölcsönhatás energiája γ-val arányos lesz, szintén megfelelően a potenciális energia változását leíró egyenletben megfogalmazott várakozásnak:

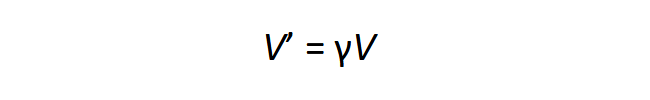
Miért éppen a cézium-133 izotóp sugárzása szolgál az időmérés alapjául?

Néhány szót még arról, hogy miért épp a cézium-133 atom hiperfinom sávját választották ki az időmérés standardjának. Az óra pontosságát az szabja meg, hogy a kibocsátott frekvencia hogyan aránylik a detektálás vonalszélességéhez. Az elektronok egyes látható és UV-átmenetei a nagy frekvencia miatt elvileg kedvezőbbek lehetnek, de a detektálási nehézségek miatt a technikai alkalmazásoknál megfelelőbb a mikrohullámú tartományt is elérő hiperfinom átmenetek gerjesztése. Ehhez viszont elengedhetetlen, hogy az átmenet egyetlen s típusú (nulla pálya-impulzusmomentumú) elektrontól származzon. Az ilyen pályák jelentős sűrűséggel fordulnak elő az atommag belsejében is, a többi pálya viszont irányfüggő hiperfinom felhasadást okoz, amely kiszélesíti a rezonanciavonalat. A céziumatom alapállapotban [Xe](6s) konfigurációval rendelkezik, és minél nagyobb a fő kvantumszám (itt n = 6), illetve minél nagyobb az atommag töltése, annál nagyobb az elektronsűrűség, és az általa létrehozott hiperfinom csatolás. Ezek a feltételek nem radioaktív elemek közül a nagy mágneses momentummal rendelkező cézium-133 izotóp esetén a legjobbak, és ennek köszönhetjük az atomórák rendkívüli pontosságát, amely eléri a napi 1 ns (10^-9s) hibahatárt.

Javaslat a relativitáselmélet hatásának közvetlen megfigyelésére

Nem csak a hosszabb élettartam alapján figyelhetünk meg különbséget két inerciarendszer között. Képzeljünk el egy űrhajót, ami nagy sebességgel (a fénysebesség 40 százalékával) közelít a Föld felé, és elhalad mellette. Az onnan küldött fényjelek a közeledéskor kék eltolódást, távolodáskor vöröseltolódást mutatnak az optikai Doppler-effektus miatt. Van azonban egy különleges pillanat, amikor az űrhajó épp elhalad mellettünk, és az átváltás bekövetkezik. Ha az űrhajó épp ekkor bocsát ki egy vörös impulzust (440 THz), azt a földi megfigyelő kéknek (630 THz) láthatja, viszont a Földről indított vörös fény az űrhajóban már nem látható szabad szemmel, mert átcsúszik az infravörös (307 THz) tartományba. Ha viszont a Földről kék fényt indítunk, az az űrhajóban már vörös lesz. Mi a magyarázat?

Színérzékelés és fehérjék

Hogyan tudjuk megkülönböztetni a színeket? Ennek kulcsa három specifikus fehérje, melyek különböző energiájú fényt nyelhetnek el, és amikor megváltoztatják geometriájukat, az eredeti, görbült alak kiegyenesedik, és, akár egy kapcsoló, elektronokat indít el az idegpályákon az agy felé. A három különböző fehérjétől származó üzenetből alakítja ki agyunk a szivárvány összes színét. A felgyorsított űrhajóban a felvett energia mértékében minden együtt változik, ami a fizika, a kémia és biofizika törvényeire egyaránt vonatkozik. A vörös fény energiája így nagyobb lesz, de az abszorbeáló fehérjék ezt a megnövekedett energiát nyelik el, emiatt az űrhajóban nem vesszük észre a változást. A földi rendszerben viszont a szemünkben levő fehérjék, illetve műszereink alacsonyabb energiaszintre vannak beállítva, ezért a kék színre érzékeny fehérje fogja érzékelni az űrhajóból érkező vörös fényt. Ugyanakkor a Földről küldött fényüzenet esetén az űrhajó utasainak szemében a vörös színre érzékeny fehérje fogja elnyelni a Földről küldött kék színű fényt. Ez a szemléletes kísérlet nem kivitelezhető a gyorsításhoz szükséges óriási mennyiségű energia miatt, de egy űrállomás és egy geostacionárius pályára állított űrszonda segítségével adódna reális lehetőség egy hasonló kísérlet elvégzésére. Amikor az űrállomás egy ilyen szonda alatt éppen elhalad, üzenetet válthatnának fényjelek segítségével. Bár a frekvenciaeltolódás jóval kisebb lenne, a spektrométerek jó felbontóképessége miatt kimutatható lenne ez a változás; igaz, ekkor a gravitáció dilatációs hatását is figyelembe kellene venni. Egy ilyen kísérlet fényes bizonyítékot adhatna a relativitáselméletre is.

A tömegközépponti rendszer kulcsszerepe

Ismét hangsúlyozni kell, hogy szükség van egy körfolyamatra a két inerciarendszer között. Az űrhajó a Földről indul el, és a fényjelekkel történő üzenetváltás zárja le a körfolyamatot. Miért éppen a Földhöz kötött inerciarendszer az irányadó a sebesség megállapításában? Ez az impulzus megmaradáshoz kapcsolódik, mert a rendszer teljes impulzusát belső erőhatások nem változtathatják meg. A teljes rendszerben a Föld, az űrhajó és a kibocsátott rakéták szerepelnek, sőt a Napot is számításba kell venni a gravitációs kölcsönhatás miatt. (Ez utóbbi akkor játszik szerepet, ha a Földet különböző irányban kerüljük meg, példa rá a Hafele-Keating kísérlet, ahol atomórákkal kimutatták az idődilatáció által okozott eltérést.) A teljes rendszer tömegközéppontja választja ki a kitüntetett inerciarendszert, amit lényegében a Föld, illetve a Nap helyzete határoz meg óriási tömegük miatt. Az inerciarendszerek ekvivalenciájáról azért beszélhetünk, mert a relativitáselmélet transzformációs szabályai bármilyen tömegeloszlás mellett érvényesek. Mi gondolatban oda tehetjük a tömegközéppontot, ahová csak akarjuk, akár azt is elképzelhetjük, hogy az űrhajó tömege jóval nagyobb, mint az egész Földé, vagy a naprendszeré. Konkrét esetekhez azonban konkrét tömegeloszlás tartozik, ami kiemel egy inerciarendszert a lehetőségek közül. Az űrhajó energiafölvétele – és ezáltal a benne lejátszódó fizikai folyamatok üteme – szempontjából az a meghatározó, hogy mekkora az űrhajó sebessége a konkrét rendszer tömegközéppontjához viszonyítva.

Így oldhatjuk fel a dilemmát az inerciarendszerek ekvivalenciájának kérdésében, és juthatunk közelebb a látszat és valóság változó viszonyának megértéséhez.

A szerző fizikus, a BME és az ELTE címzetes egyetemi tanára. Kalandozások a fizikában sorozatának korábbi írásai itt, tudósportréi itt olvashatók.

Kapcsolódó cikkek a Qubiten:

link Forrás

link Forrás