Közel a fizika leghíresebb paradoxonjának megoldása – vagy mégsem?
„Közel vagyunk a fizika leghíresebb paradoxonjának megoldásához” – ezzel a csábító címmel jelent meg George Musser beszámolója a Quanta Magazine-ban az elméleti fizikusokat jelenleg legjobban izgató, az elmúlt két évben rendkívüli mértékben felizzó kérdésről.
A jelen írás szerzője csak távoli megfigyelője ennek a tudományos törekvésnek, és az ismertetés során közbeszúrt – időnként szkeptikus – megjegyzésekkel egészíti ki a beszámolót.
A fizika nagy paradoxonja
Először is azt nézzük meg, hogy mi az a paradoxon, amiről a cikk szól. Az alap az időbeli folyamatok iránya. A gravitáció, az elektromágnesesség és a kvantummechanika törvényeit az jellemzi, hogy a folyamatok megfordíthatók, ezt nevezzük időtükrözési szimmetriának. A fekete lyukak azonban ellentmondanak ennek a szabálynak, mert amit egyszer lenyeltek, az ott is marad. Tehát a fekete lyukak irreverzibilis folyamatai ütköznek a fizika reverzibilis törvényeivel.
Kezdő lépések a feloldásra
Ezt a paradoxont enyhítette Stephen Hawking felfedezése az 1970-es években. Hawking kimutatta, hogy a fekete lyukak is képesek sugározni, és így legalább részben visszaadják a korábban elnyelt sugárzást. Ez azonban még nem oldotta fel a paradoxont, mert csak a fekete lyuk peremvidékéről szabadul ki a sugárzás, de a mélyben elnyelt anyag továbbra is ott marad, azaz a megfordíthatóság kritériuma továbbra sem teljesül.
Ez a probléma foglalkoztatta a kanadai Albertai Egyetemen fizikusát, Don Page-t, aki korábban Hawking tanítványa volt. Page továbblépett Hawking elméletén, és 1992-ben felvetette a fekete lyuk teljes „elpárolgásának” ötletét, amelynek során a véletlenszerű kvantumfolyamatok kívülről befelé haladva teljesen leépítik a fekete lyukat. Ez még önmagában nem oldja meg a paradoxont, mert a kiáramló részecskék szerkezete nem tükrözi az elnyelt anyagét. Például, ha egy 100 kilós űrhajóst elnyelt a fekete lyuk, a kiáramló 100 kiló anyagban már nem mondhatjuk meg, hogy ez az űrhajóstól vagy egy ólomtömbtől származik-e. Hiába bocsátja tehát ki az összes elnyelt anyagot a fekete lyuk az utolsó grammig, csupán a részecskék véletlenszerű halmaza jön létre, amiből nem rekonstruálható az elnyelt anyagok szerkezete. Más szóval az irreverzibilitás fennmarad, ellentétben a kvantummechanika szimmetria törvényével.
Page koncepciója
Hawking és munkatársai azt az álláspontot fogadták el, hogy a fekete lyukhoz irreverzibilis folyamatok tartoznak, tehát a kvantummechanika szimmetriatörvényén kellene valamit igazítani. Page azonban nem így gondolkozott: szakítva korábbi patrónusával még 1980-ban kijelentette, hogy szerinte a fekete lyukból kibocsátott anyag valamilyen módon megőrzi a benne elnyelt objektumok információját. Ez a kijelentése megosztotta az elméleti fizikusok táborát; azok, akik az általános relativitáselmélet talaján álltak, továbbra is elfogadták Hawking felfogását, a részecskefizikusok viszont már Page felvetését találták elfogadhatónak.
A kvantumösszefonódás koncepciója
Page azonban úgy látta, hogy mindkét csoport figyelmen kívül hagy valamit: nemcsak az számít, hogy mi történik a fekete lyuk eltűnésekor, hanem az is fontos, hogy milyen út vezet odáig. Elgondolásához segítségül hívta a kvantumösszefonódás koncepcióját. Itt most egy kis kitérőre van szükség, hogy megvilágítsuk, mit is kell érteni ez alatt. A kvantummechanika határozatlansági relációja szerint bizonyos fizikai mennyiségek egyidejűleg nem mérhetők meg teljes pontossággal, például a pozíció és az impulzus hibájának szorzata nem lehet kisebb a ħ Planck-állandónál. Ugyanez vonatkozik a részecskék spinjének két komponensének mérésére is; fotonoknál ez a polarizáció mérésénél jelentkezik.
Egy francia fizikus, Alain Aspect volt az első, aki a kibocsátási helytől számítva egyforma távolságban határozta meg két – egyetlen reakcióban képződő – foton polarizációját, és egyértelmű kapcsolatot kapott a két foton polarizációja között, ami arra mutatott, hogy vagy a határozatlansági relációval van baj, vagy pedig nem igaz, hogy két távoli objektum között nem jöhet létre kölcsönhatás gyorsabban, mint a fénysebesség.
A határozatlansági reláció ugyanis megkövetelné, hogy az egyik foton polarizációjának megváltoztatása (ami a mérésnél mindig bekövetkezik) egyúttal a másik, távoli foton polarizációját is megváltoztassa, mégpedig késleltetés nélkül. Az ellentmondás feloldására született meg az összefonódott kvantumállapotok koncepciója. Ez azt jelenti, hogy amikor két részecskét egyidejűleg hozunk létre, akkor ezek később is egyetlen összefonódott állapotban maradnak, és ha az egyiknek megváltoztatjuk az állapotát, az magával hozza, hogy a másik részecske állapota tükörszerűen változik. Ebből született meg a teleportálás gondolata is: ha valahol létrejött egy ilyen összefonódott állapot, és abból az egyik részecske állapotát megváltoztatjuk itt a Földön, akkor annak párja valahol – akár egy távoli galaxisban – tükrözni fogja az átalakulást.
Az elveszett információ dekódolása
Page koncepciója úgy fogja fel a fekete lyukból kiáramló sugárzást, hogy annak összefonódott párja ott van a fekete lyukban, és a mi feladatunk, hogy feltárjuk ezt a kapcsolatot, és ennek segítségével dekódoljuk a látszólag véletlenszerű struktúrát. A folyamat a hologramok dekódolásához hasonlítható, amikor egy véletlenszerűnek látszó ponthalmazból felépítjük az eredeti struktúrát. Külön-külön a fekete lyuk belső szerkezete és a kibocsátott anyag és sugárzás is véletlenszerű alakot ölt, de összekapcsolások már megőrzi az információt.
Az információ tehát nem vész el, csak dekódolni kell.
Az összefonódási entrópia
Az információ mennyiségének jellemzésére Page bevezette az összefonódási entrópia fogalmát. Az entrópia fogalma a termodinamikából származik, és azt jellemzi, hogy a rendezett struktúrák milyen mértékben alakultak át rendezetlen, és ezért sokkal többféleképp megvalósulható mikroállapotban, vagy másképpen fogalmazva, az energia különböző formáinak egymásba alakulása során milyen mértékben nő meg a molekulák rendezetlen hőmozgása. Ehhez kapcsolódik a rendszer információtartalma is, hiszen egy rendezetlen állapot egzakt leírásához sokkal több információra van szükség, mint amikor egy rendezett struktúrát akarunk jellemezni.
Page a kvantumösszefonódással leírt rendszerben kívánta meghatározni az entrópiaváltozást. Ha nem vész el a folyamat során információ, akkor az entrópia sem változik. Amíg nem indul el a fekete lyuk Hawking-sugárzása, nincs összefonódás sem, ezért a hozzáköthető entrópia is nulla. A végállapotban szintén nincs összefonódás, mert megszűnik a fekete lyuk, így ekkor is nulla a keresett entrópia. Viszont a sugárzás elindulása után az entrópia növekedni fog, amely később csak úgy térhet vissza a nulla értékhez, ha valahol a bomlási folyamat közepén megfordul a trend, és csökkenni kezd az entrópia. Az egész folyamat tehát egy fordított V alakot ölt. Page-nek tehát volt egy koncepciója, de ezt valahogy igazolni kellett, matematikailag kiindulva a fekete lyukak fizikájából. Ez viszont irtózatosan nehéz feladatnak bizonyult, és nem is sikerült az elmúlt 30 év során.
A gravitáció kvantumelméletének keresése és a húrelméletek
A nagy fordulat két évvel ezelőtt következett be, amikor rendkívül széles nemzetközi összefogással, egymással versenyezve és összefogva születtek számítások annak érdekében, hogy igazolják a Page által feltételezett modellt.
A nehézségek részben matematikai természetűek, részben alapvető fizikai koncepciók összekapcsolásából származnak, és emellett még nagyszámú közelítést is szükségessé tesznek Az eljárás bemutatására csak vázlatosan vállalkozunk. Az egyik nehéz elvi feladat a kvantumelmélet összekapcsolása a gravitációval. Az elméleti fizikia immár száz éve küszködik azzal a kérdéssel, hogy miként lehetne a gravitációt beilleszteni a kvantumelméletek közé. Minden kölcsönhatást bozonok közvetítenek, ezek az elektromágneses kölcsönhatásban a fotonok, a gyenge kölcsönhatásban a W és Z bozonok, az atommagokat és a hadronokat összeforrasztó erős kölcsönhatásban a gluonok. (Hadron az összefoglaló neve a mezon és barion típusú elemi részecskéknek, legismertebb közülük a proton és neutron). A felsorolt mezőelméletek mintájára keresik a gravitációt közvetítő bozont, amit gravitonnak neveztek el. A probléma azonban az, hogy ilyen bozon létezését semmilyen kísérlet sem támasztotta alá, és az elméleti próbálkozások sem hoztak meggyőző eredményt. A próbálkozások elméletek sorának kidolgozásához vezettek, amelyek kiléptek a megszokott háromdimenziós térből, feltételezve további térdimenziókat: ezek a különböző húr- és M- (membrán) elméletek.
A kiinduló ötletet Theodor Kaluza próbálkozása adta. A német matematikus és fizikus bevezetett egy negyedik térdimenziót, amelyben Einstein gravitációs egyenlete alapot teremtett az elektromágnesesség Maxwell-egyenleteinek értelmezéséhez is. Az ígéretes eljárással azonban baj volt, amikor a kölcsönhatásokat kvantumok segítségévek akarták leírni. Emiatt aztán további térdimenziókkal kezdtek próbálkozni, amelyek száma gyorsan emelkedni kezdett, olyannyira, hogy egyes elméletek már 24 dimenziónál tartanak.
Vitathatatlan azonban, hogy vannak részeredmények: a leggyakrabban használt modell az AdS/CFT korrespondencia nevet viseli. (Teljes nevén anti-de Sitter/conformal field theory, ahol az AdS felel meg a kvantumgravitációnak, a CFT a különböző mezőelméleteknek, tehát az elektrogyenge és erős kölcsönhatásnak.)
A Page-görbét leíró próbálkozások is ezen alapulnak.
A húrelmélet jelenlegi helyzete
Érdemes még néhány szót szólni a sokdimenziós húrelméletek jelenlegi helyzetéről. Vezető egyetemeken és elméleti műhelyekben ez most a legaktívabb és legtöbb támogatásban részesülő kutatási irány, rengeteg neves kutató dolgozik rajta, és számos PhD-dolgozat születik meg minden évben. Az eredmények mégsem biztatóak. Lee Smolin magyarul is megjelent Mi a gubanc a fizikával? című könyvében igen kritikusan értékeli a helyzetet.
A magam részéről azt is kérdésesnek tartom, hogy valóban szükséges-e a gravitáció elméletét is kvantumos alapokra helyezni. Lehet, hogy a fizikatörténet megismétli önmagát?
Korábban rengetegen próbálkoztak örökmozgó építésével. A kudarcok tanulságait vonta le a termodinamika, amikor legfontosabb törvényeiben kimondta, hogy perpetuum mobile nem építhető, ami annak felel meg, hogy izolált rendszerekben az entrópia csak növekedhet. Az immár száz éve folyó kvantumegyesítési erőfeszítések kudarcából akár arra is következtethetünk, hogy a gravitációs kölcsönhatás egyszerűen nem kvantumos jelenség.
A Page-elmélet igazolási kísérletei: húrelméleti közelítés
De vegyük sorra a Page modell igazolására végzett számításokat, amelynek egyes lépéseit más és más kutatóhelyek publikálták! Mindenekelőtt azt kellett tisztázni, hogyan és miért „párolog el” a fekete lyuk. Kiindulásként egy olyan univerzum képét rajzolták fel, amelyet körülvesz egy határfelület. A belső világ nem különbözik a megszokott univerzumtól, ott van benne a szokásos anyag, amit a gravitációs erők mozgatnak. A határréteg is egy önálló univerzum, amelyben a kvantumhatások működnek. A két világ nagyon különböző, de egymásnak pontosan megfeleltethető, mégpedig hasonló módon, ahogy a húrelmélet leképezi a két világot az AdS/CFT modellben. Ezt a duális modellt alkalmazzák a fekete lyukra is, ahol a külső határrétegben a kvantumvilág szimmetriája megőrzi az információt, és hasonló történik a gravitáció által igazgatott belső zónában is.
Az AdS/CFT modell alkalmazásánál le kellett küzdeni egy problémát, mert az ott definiált fekete lyuk nem „párolog el” a kibocsátott és újra elnyelt sugárzás miatti egyensúly miatt. Bevezettek ezért a számításba egy „gőzszelepet”, amely kiengedi a „gőzt”, azaz a sugárzást, de megakadályozza annak visszatérését. Az erre alapozott számítási modellben a kvantumeffektusok szappanbuborék módjára fújják fel a fekete lyukat. A számítások szerint azonban ez a buborék nem marad gömbszerű, hanem fokozatosan behorpad, majd két részre hasítja az eredeti belső struktúrát. A számítások másik eredménye a külső határréteg felületére vonatkozik, amelyet arányosnak találtak az összefonódási entrópiával. Az így számolt entrópia kezdetben Hawking számításainak megfelelően növekedett. Azonban a későbbi szakaszban a kvantumtulajdonságokat hordozó felület csökkenni kezd, és magával hozza a teljes entrópia csökkenését is. Ez már eltérést mutat Hawking számításaitól, és jelzi az univerzum kettéválását, amelynek összehúzódó eseményhorizontja kiváltja az összefonódási entrópia csökkenését, és így előállítja a Page által előrelátott, fordított V alakú változást. Ez az eredmény már mutatja, hogyan távozik az információ a fekete lyukból. Viszont az információ erősen kódolt, és meg kell találni a kulcsot, hogy visszanyerhessük a fekete lyuk által látszólag megsemmisített információt.
A kulcs megtalálását az AdS/CFT világban úgy érjük el, hogy ott a fekete lyukat nem gömbszerű alakzatnak, hanem egy rövid vonal formájában adjuk meg. De hogyan működhet a gravitáció a leegyszerűsített egydimenziós alakzatban? Ennek feloldására vizsgálták meg a kétdimenziós modellt, amely megnyugtató összhangot mutatott az előbbiekkel.
Más számítások már a fekete lyukból kibocsátott sugárzásra terelték a hangsúlyt, és kimutatták, hogy ennek változása is követi a Page-szabályt, illetve arra is rámutattak, hogy az információ a fekete lyukból áttevődik a külső sugárzási térbe. Azt viszont már nem tudták megmondani, hogy mi a konkrét útja az információ átadásnak. A számítások meglepő eredménye, hogy csak kezdetben van szó kifelé történő sugárzásról, a későbbi szakaszban a határzóna rendeződik át, amely miatt a belső részecskék már nem lesznek a fekete lyuk alkotói. Valójában épp ez az összefonódási entrópia csökkenésének oka, mert sugárzás nélkül nem jönnek létre kvantumösszefonódások sem.
Ezen a ponton a Quanta Magazine szerzője is kifejti kétkedését: mit jelent az, hogy a részecskék ott maradnak a fekete lyukban, de mégsem alkotói többé? Erre a megkérdezett fizikusok válasz helyett csak néztek a nagyvilágba, viszont nekünk, magyaroknak Trianon óta ez a magyarázat könnyen érthető.
Fekete és féreglyukak
A számítások próbaköveként alkalmazott AdS/CFT duális világmodell meglehetősen kiagyaltnak tűnik, ezért felvetődik a kérdés, hogyan lehetne mégis ennél reálisabb képet formálni a fekete lyukakról? Itt nyúltak vissza a kutatók Richard Feynman koncepciójához, aki az 1940-es években dolgozta ki az útintegrálokra alapozott módszerét az elektromágneses kölcsönhatás magyarázatára. Ennek lényege, hogy amikor a részecske eljut az A pontból a B-be, közben minden lehetséges utat kipróbál, és azt fogja választani, ami a valószínűségi súlyok összegeként a legnagyobbnak adódik.
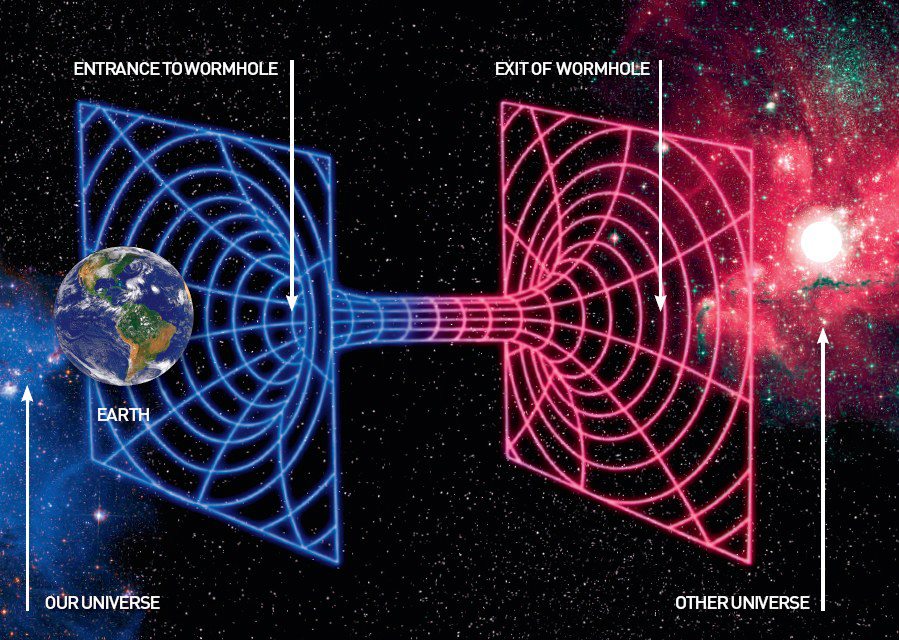
Ez így van a szokásos esetekben, de mi történik, ha hirtelen megváltoznak a valószínűségi súlyok? Ekkor a részecske már a szokásostól eltérő pályára fog ugrani. A módszer ragyogóan működik a részecskemozgások leírásában. Nem lehetne alkalmazni ezt a gravitáció kvantumos elméletében is? – vetették fel a fizikusok még az ötvenes években. Ez azt jelenti, hogy a téridőstruktúrák sokasága létezik más és más valószínűséggel, és ezek eredője vezet el a gravitáció által vezérelt mozgásokhoz. Feynman és Hawking is komoly erőfeszítéseket tett arra, hogy kifejlesszék a módszert, de a gravitációs útintegrálási módszer nem hozta meg a kívánt eredményt. Emiatt került elő az ötlet az einsteini relativitáselméletből: próbálják meg a fekete lyukat olyan féreglyukként leírni, amely közvetlen átjárást hoz létre távoli csillagok között.
A modellszámításokat a legesélyesebb topológiákra korlátozták, ahol az útintegrálok nyeregpontokat találtak, és nekiláttak az összefonódási entrópia meghatározásának. Ezt a mennyiséget egy mátrix logaritmusa fejezi ki, de gondot okoz, hogy ez a mátrix nem ismert. Emiatt kényszerültek a kutatók egy újabb matematikai trükk bevetésére. Ezt arra alapozták, hogy a számításhoz nincs szükség a mátrix valamennyi elemére. Elképzelték ismételt mérések sokaságát, majd olyan kombinációkat választottak ki, amelyek megtartották az eredeti információt. Ez egyfajta replikaeljárás, ahol úgy ellenőrizzük, hogy nem hamis-e az érme, hogy sokszor feldobjuk, és megnézzük, hogy a fej és az írás egyformán gyakori-e. De ehelyett úgy is eljárhatunk, hogy egyszerre két pénzérmét dobunk fel, és azt vizsgáljuk, hogy milyen gyakran egyezik vagy különbözik a két érme oldala. Ha ebben nincs eltérés, akkor az érmék nem hamisak, azaz akkor is megállapíthatjuk, hogy nincs-e csalás, ha nem tudjuk eleve, mekkora a valószínűsége a különböző eseteknek. Lényegében ez a helyzet az entrópia számításnál, ott ugyanis nem ismerjük a számításhoz szükséges mátrixot.
Ez ugyan csak egy matematikai trükknek látszik, de megvan a fizikai realitása is. A gravitációs útintegrálok nem különböztetik meg a fekete lyukat a replikától, de olyan topológiákat hoznak létre, amelyek megalkotják a Hawking-sugárzással körbevett fekete lyukakat. Az útintegrálokban szereplő súlyfaktorok fordítottan arányosak a fekete lyukak és a féreglyukak összefonódási entrópiájával, ezért a féreglyukak kezdeti nagy entrópiája miatt járulékuk elhanyagolható a fekete lyukból kiáradó sugárzáshoz képest. Ahogy a féreglyuk entrópiája csökken, a sugárzásé nő, és mivel a súlyfüggés fordított, fokozatosan a féreglyukak járuléka lesz a domináns.
Viszont ezt a kétféle geometria közötti arányváltozást már nem tudja leírni a klasszikus általános relativitáselmélet, ez ugyanis alapvetően kvantált folyamat. Erre az elvre alapozva két független kutatógárda is kimutatta, hogy tényleg helyes az entrópia változás Page által feltételezett görbéje. A levezetés ezáltal eljutott odáig, hogy a sugárzás képes elrejteni magába az információt, de hátravan még annak megfejtése, hogy miként menekíthető ki onnan.
A kvantumszámítógép bevetése
A kérdés megválaszolására a kutatók azt találták ki, hogy a fekete lyukból kiáramló sugárzás összes információját betöltik egy hatalmas kvantumszámítógépbe, és annak segítségével hajtják végre a fekete lyuk szimulációját. Ez az ötlet azonban újabb csavart hozott a történetbe.
A fekete lyuk jelenléte nagy mértékben összekuszálja a sugárzást; hasonló történik a kvantumkomputerből kijövő információval is. A szimuláció során ez az összekuszálódás geometriai jelleget ölt, összekapcsolva a szimulált fekete lyukat az eredetivel. Ezt az összekapcsolódást jeleníti meg a féreglyuk replikája. Erre a féreglyukra úgy kell tekinteni, mint titkos átjáróra, amely kimenekíti az információt a fekete lyuk belsejéből.
Féreglyuk és nem lokális kölcsönhatás
Mekkora a fizikai realitásuk ezeknek a féreglyukaknak? A kérdés még nyitott a fizikusok táborában is. Sokan úgy tekintenek a féreglyukakra, mint a nem lokális fizikai kölcsönhatások egyik formájára, hivatkozva a kvantum-teleportálás koncepciójára is. (Nem lokális a kölcsönhatás, ha a tér két elkülönült pontja között jön létre – anélkül, hogy ezt valamilyen részecske, például foton, közvetítené.) Ez a felfogás viszont szembemegy Einstein eredeti elképzelésével, aki épp azért dolgozta ki elméletét, hogy kiküszöbölje belőle a nem lokális kölcsönhatást. Az elmélet szerint a gravitációs hatás is az időben terjed, mégpedig ugyanúgy fénysebességgel, mint az elektromágnesesség. Jelenleg viszont a fizikusok között elterjedőben van a nézet, hogy a szimmetria – ami alapvető a relativitáselméletben is – előidézhet nem lokális effektusokat. Felmerül a sejtés, hogy talán nem is a téridő a valóság legmélyebb szintje: lehet az alatt is valami, ami nem térszerű és nem időszerű. Ebbe az irányba mutat a húrelmélet és annak alternatívája, a féreglyukak feltételezése is.
Szkeptikus nézetek
Sok fizikus szkeptikus a fent vázolt elmélettel, mert túl sok benne az önkényes feltételezés és egyszerűsítés. Az egész egy olyan logikai építmény, amelynek ha az egyik vagy másik eleme hibás, az egész kártyavárként összeomolhat. Nézzünk néhány konkrét észrevételt! A feketelyuk-replikák esetén feltételezi a számítás, hogy bármilyen geometriával össze lehet kötni őket, de kérdés, hogy ez nem ellenkezik-e a kvantumszabályokkal. Mások szerint az alkalmazott szemiklasszikus számítások nem adhatnak reális megoldást a kvantumelv és a gravitáció összekapcsolására. A felvetett kérdésre csak egy valódi kvantumgravitációs elmélet adhat megbízható választ. A számítások rendkívüli bonyolultsága miatt még ahhoz is idő kell, hogy az esetleges hibák kiderüljenek.
Az elmélet ismertetése egy képzelt párbeszéddel fejeződik be. Ha az űrhajós megkérdezi, biztosan kijut-e majd a fekete lyukból, arra igen a válasz. De ha azt is megkérdezi, hogyan, arra a válasz már az, hogy fogalmunk sincs.
Ezen írás szerzője ehhez még hozzáteszi: élve biztosan nem fog kijutni, mert a hatalmas gravitáció már azelőtt kioltja életét, hogy a fekete lyuk beszippantaná.
A szerző fizikus, a BME és az ELTE címzetes egyetemi tanára. A Kalandozások a fizikában címen a Qubiten futó sorozatának korábbi írásai itt, tudósportréi pedig itt találhatók.
Korábbi kapcsolódó cikkeink: