Ész Ventura: Ez az örökmozgó túl szép ahhoz, hogy igaz legyen
92. feladványunkban egy örökmozgó működésének képtelenségét kellett megmutatni. Az egyszerű szerkezet lényegében egy U alakú cső, amelynek bal oldali szára magasabb, mint a jobb oldali. A magasabb szárba vizet kell tölteni, míg a másik oldalra egy víznél nagyobb sűrűségű és a vízzel nem keveredő folyadékot. A közlekedőedényekről tanultak alapján a bal oldalon magasabban fog állni a víz szintje, ahogy azt az ábra is mutatja. A szerkezethez tartoznak még fagolyók, amelyek sűrűsége kisebb mindkét folyadék sűrűségénél. A jobb oldali csőbe több golyót is be kell önteni, ezek átmérője csak picit kisebb, mint a cső átmérője, ezért a golyók egymáson helyezkednek el és egymást nyomják. A jobb oldali csőben annyi golyónak kell lennie, hogy a legalsó már átbillenjen az U alakú cső másik oldalára. Az átbukkanó golyó felúszik, és mivel a víz felszíne magasabban van, ezért a feltételezés szerint vissza tud esni a golyóoszlop tetejére, esés közben pedig akár egy kis lapátkereket is megforgathat, amivel hasznos munkát tud végezni. Miután a golyó visszaesik a többi tetejére, a legalsó golyó megint lenyomódik annyira, hogy alul átbukkanjon, és kezdődik a ciklus elölről. Hol lehet a hiba a gondolatmenetben?
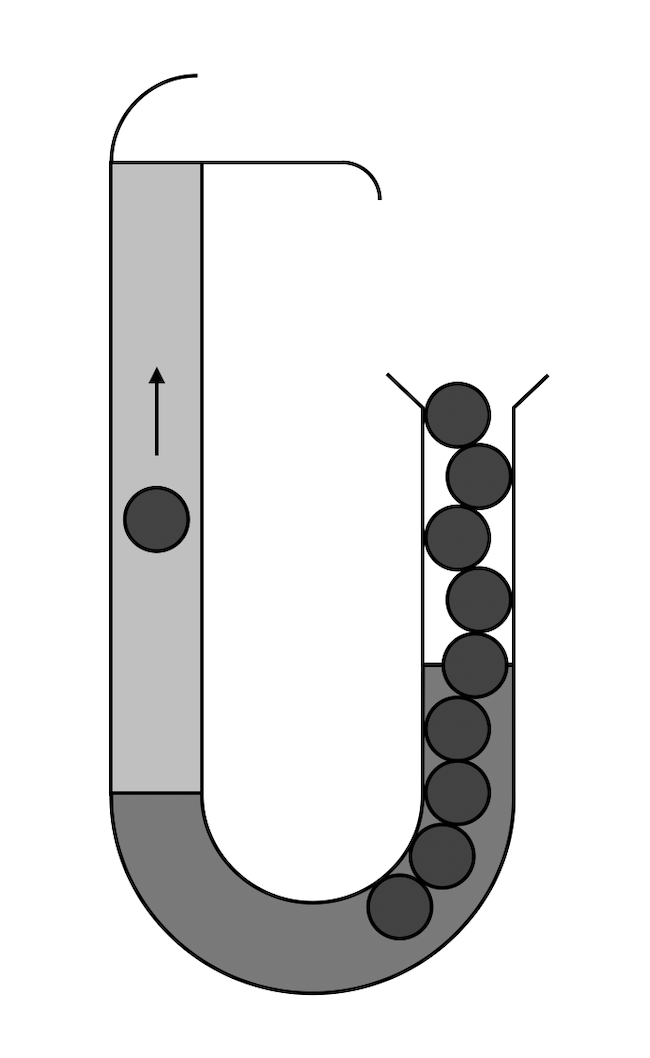
Meg fogjuk mutatni, hogy az illusztráció félrevezető volt, ugyanis ahhoz, hogy a golyósor lenyomja annyira a legalsó golyót, hogy az átbillenjen a másik oldalra, ahhoz magasabb oszlop kéne, mint a teljes bal oldali szár, vagyis az átbillenő golyó hiába úszna fel, nem tudna feljutni a golyóoszlop tetejére, így pedig nem tudna kialakulni folyton ismétlődő ciklus.
Rögzítsük a jobb oldali folyadéknak és a golyóknak a sűrűségét, ezek legyenek rendre R és r < R. Ha azt akarjuk belátni, hogy a golyóoszlop magasága túllépi a bal oldali szár magasságát, akkor a legrosszabb eset számunkra az, amikor a bal oldali szár a lehető legmagasabb. Ez a szár hidrosztatikailag egyensúlyt tart a fix sűrűségű jobb oldali folyadékoszloppal, ezért akkor lesz a legmagasabb, amikor a sűrűsége a lehető legkisebb. Legkisebb viszont akkor lehet, ha a golyó sűrűségénél csak egy hangyányival nagyobb, hiszen a golyó felúszik ebben a folyadékban, annak pedig feltétele, hogy a golyó legyen a könnyebb, ahogy az a feladatban is szerepelt. Az egyszerűség kedvéért tehát feltehetjük, hogy a könnyebb folyadék sűrűsége és a golyók sűrűsége lényegében megegyezik. Ha ebben az esetben is meg tudjuk mutatni, hogy a golyóoszlop magasabb, mint a bal oldali szár, akkor ez minden esetben igaz lesz.
Az egyszerűség kedvéért nézzük meg előbb azt, hogy ezekkel a feltételekkel mekkora golyóoszlop kell ahhoz, hogy a legalsó golyó éppen érintse a két folyadék közös határának szintjét, amit az alábbi illusztráción szaggatott piros vonallal jelöltünk.
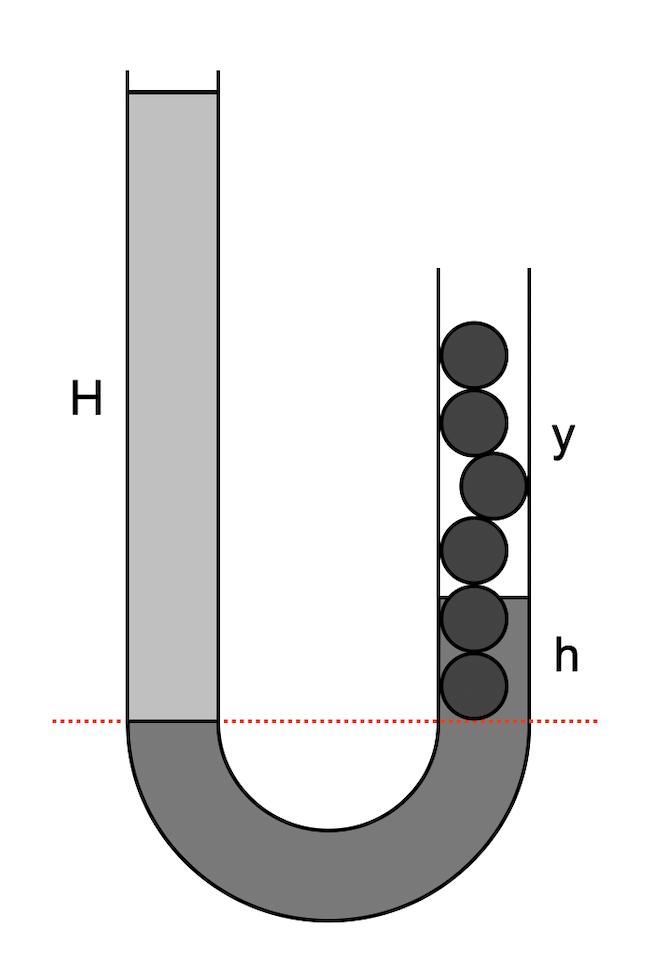
A bal oldali folyadékoszlop magassága legyen H, a jobb oldalié pedig h a két folyadék közös határának szintjétől mérve. A golyóoszlop folyadékszint feletti részének magassága pedig legyen y. Legyen továbbá a golyóoszlop folyadékba merülő részének térfogata v, a teljes golyóoszlop térfogata pedig V.
Az egyik összefüggés, amit felírhatunk, a hidrosztatikai egyensúly, ami alapján r · H = R · h, a másik pedig a golyóoszlop egyensúlya. A golyóoszlop esetében a gravitációs erő tart egyensúlyt a felhajtóerővel. A teljes golyóoszlopra ható gravitációs erő nagysága r · V · g, a felhajtóerő pedig R · v · g nagyságú, tehát a g gravitációs gyursulással egyszerűsítve az r · V = R · v összefüggéshez jutunk.
Valahogy összefüggést kéne teremtenünk a magasságok és a térfogatok között. Ha egymásra pakolt kockákról lenne szó, ahol a kockák egyik lapja vízszintes, akkor a térfogat és a magasság között egyértelmű arányosság állna fenn, az arányossági tényező pedig éppen a kocka oldalának területe lenne. A kocka térfogata ugyanis éppen az alapterület szorozva a magassággal. Golyók esetében, amik ráadásul össze-vissza helyezkedhetnek el, ilyen precíz összefüggést nem állíthatunk fel, de ha feltételezzük, hogy a golyók az oszlop mentén hasonló tömöttségben (például a lehető legtömörebben) helyezkednek el, akkor ugyancsak feltételezhetünk egy arányossági tényezőt, ami kisebb ugyan a keresztmetszetnél, de (magasabb oszlop esetén nagyjából) fix érték. Tegyük fel tehát, hogy a golyóoszlop egy x magasságú részének térfogata k · x képlettel adható meg, ahol k egy terület dimenziójú szorzó tényező. Így tehát azt írhatjuk, hogy v = k · h, és V = k · (h+y).
Felhasználva golyóoszlop egyensúlyára vonatkozó egyenletet, azt kapjuk, hogy r · k · (h+y) = R · k · h, ami alapján k-tól függetlenül adódik, hogy y = h · (R/r - 1). Viszont a hidrosztatikai egyensúly egyenletéből meg az adódik, hogy H - h = h · (R/r - 1). Azt kapjuk tehát, hogy y = H - h, vagyis az oszlop éppen a bal oldali folyadék tetejéig kell érjen ahhoz, hogy az alja elérje a folyadékhatár szintjét. Ez azonban nem elég ahhoz, hogy a legalsó golyó átbukkanjon az U alakú cső másik oldalára, még akkor sem, ha a két szár között nem íves összeköttetést, hanem egy vízszintes összekötő csövet képzelünk el. Az átbukkanáshoz ugyanis legalább egy golyónak a folyadékhatár szintje alá kéne kerülnie teljes terjedelmében.
Ezzel tehát beláttuk, hogy az elképzelés sajnos nem működik. A gyakorlatban egyébként lenne más probléma is, hiszen a golyónak ki is kellene ugrania a bal oldali folyadékoszlop tetejéről, hogy le tudjon utána esni. Ha viszont csak ez lenne a gond, akkor arra rá tudnánk segíteni egy kis energiabefektetéssel, és ha utána tényleg lefele tudna esni, akkor a végzett munkával energetikailag fenn tudnánk tartani a körfolyamatot.
További megjegyzés: ha a jobb oldali szár tetején egy tölcsért alakítunk ki, akkor több golyó is tudja nyomni a lentebb lévő golyókat, mint amennyi egy függőleges golyósorba beleférne, viszont ebben az esetben a tölcsér oldala is tartaná a golyókat, így kiderül, hogy végeredményben nem tudnánk ezen se nyerészkedni.
Kapcsolódó cikk a Qubiten: