Összeálló hatszög című feladványunkban az volt a feladat, hogy vágjunk egy szabályos hatszöget három egybevágó részre úgy, hogy az elemeket egyszerre mozgatva/csúsztatva a síkon a hatszög szétszedhető legyen, de ha egyszerre csak egy elemet mozgathatunk, akkor azt ne lehessen eltávolítani a konstrukcióból anélkül, hogy a többieken áthatolna.

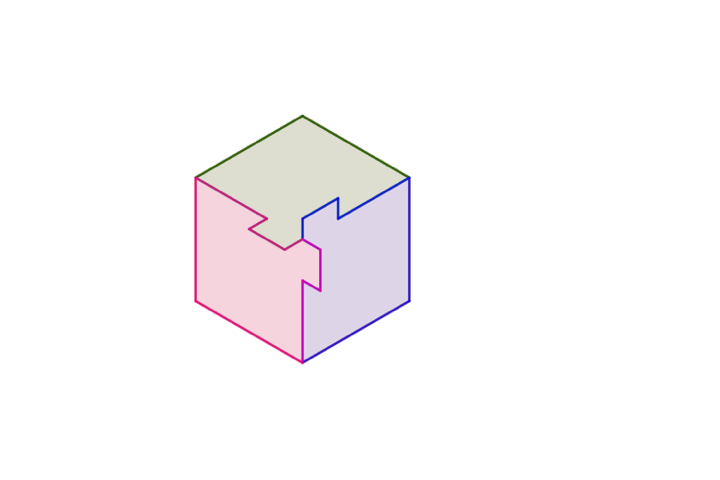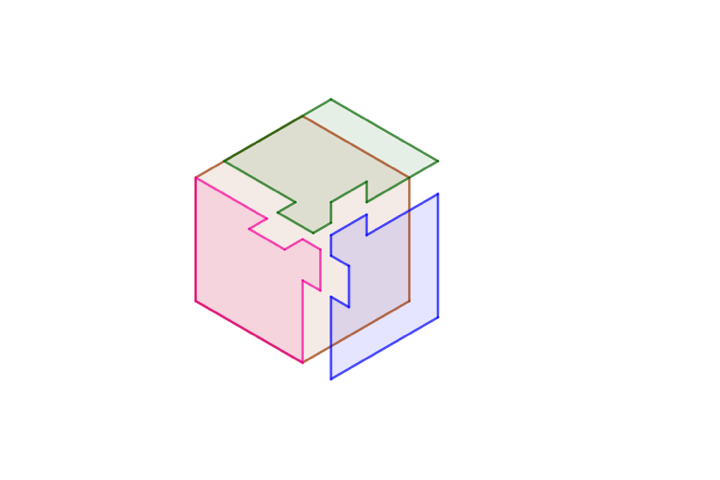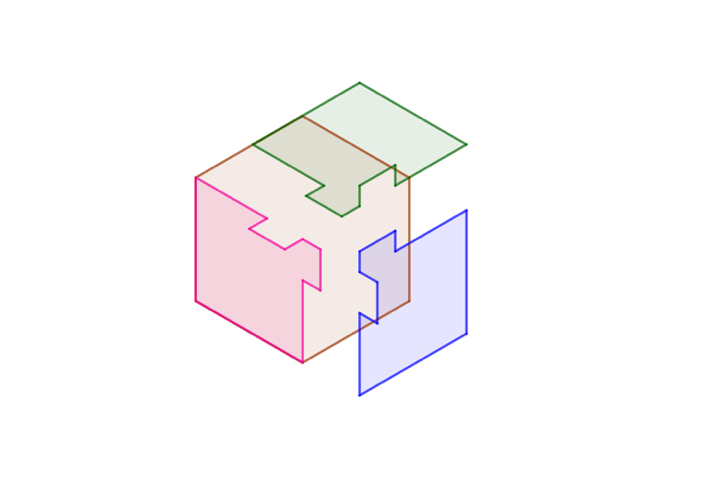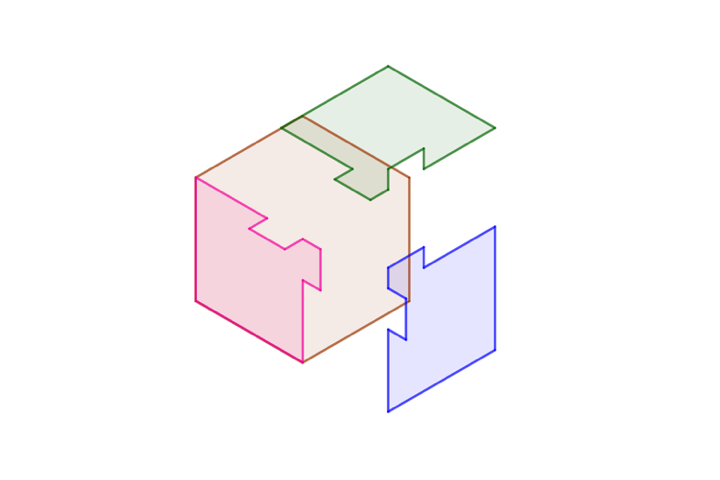
A feladványra sok különböző megoldás adható, az egyik legegyszerűbb az alábbi, amit Bodonyi Ádám illusztrációjának felhasználásával mutatunk be. A konstrukció lényege, hogy két elem rögzítése esetén a harmadikat nem tudnánk kivenni, mert az egyik szomszédos elem betüremkedő fülecskéje ezt megakadályozza, de ha egyszerre két elemet 60 fokban széttartó egyenesek mentén a megfelelő irányba mozgatunk azonos sebességgel, akkor áthatolás nélkül szétszedhető a konstrukció. Az ábrán a hegyesszögek 60 fokosak, a tompaszögek 120 fokosak, a homorú szögek pedig ezeket egészítik ki 360 fokra. Az animáció mutatja, hogy a konstrukció hogyan szedhető szét, de matematikai precizitással úgy lehet belátni, hogy nincs áthatolás, hogy az érintkező kerületek mentén egyszerűen összehasonlítjuk a szélső pontok sebességvektorait. Ha feltételezzük, hogy azonos sebességgel húzzuk őket szét, akkor belátható, hogy az idomok érintkező szélei vagy együtt mozognak egy ideig, vagy távolodnak egymástól.

Kapcsolódó cikk a Qubiten: