Biztonságos szoba című feladványunkban az volt a kérdés, hogy mekkora az a legkisebb négyzet alakú szoba, ahol le tudunk ültetni három pontszerűnek tekintett embert úgy, hogy bármely kettő távolsága legalább 5 méter legyen. Ha megfelelő módon tekintünk erre a kérdésre, akkor rájöhetünk, hogy ez lényegében nem más, mint a körpakolás problémája négyzetbe, és erre a konkrét esetre vonatkozóan a megoldást megtalálhatjuk a Wikipédián is, ezért is volt csak egykoponyás a feladvány.

Rajzoljunk az emberek köré 2,5 méter sugarú köröket. Ha két kör metszi egymást, akkor biztosak lehetünk abban, hogy a hozzájuk tartozó két ember 5 méternél közelebb van egymáshoz, ha viszont a körök nem metszik vagy legfeljebb érintik egymást, akkor az emberek közti távolság legalább 5 méter lesz, ahogy szeretnénk. A feladat tehát az, hogy a lehető legkisebb négyzetbe elhelyezzünk három körközéppontot úgy, hogy az ezen pontok köré írt 2,5 méter sugarú körök ne metsszék, legfeljebb csak érintsék egymást. A körök természetesen kilóghatnak a négyzetből, mivel azonban középpontjuk a négyzetben van, legfeljebb 2,5 méterre lóghatnak ki. Ha tehát megtaláljuk a legkisebb négyzet alakú szobát, ami teljesíti a feladat feltételeit, akkor a szobánál minden irányban 2,5 méterrel nagyobb négyzet tartalmazni fog három 2,5 méter sugarú kört átfedésmentesen, és ez lesz a legkisebb ilyen négyzet. Ha pedig fordítva gondolkodunk, és megtaláljuk a legkisebb négyzetet, amibe három 2,5 méter sugarú kör átfedésmentesen bepakolható, akkor az 5 méterrel kisebb oldalú négyzet lesz a keresett szoba mérete.

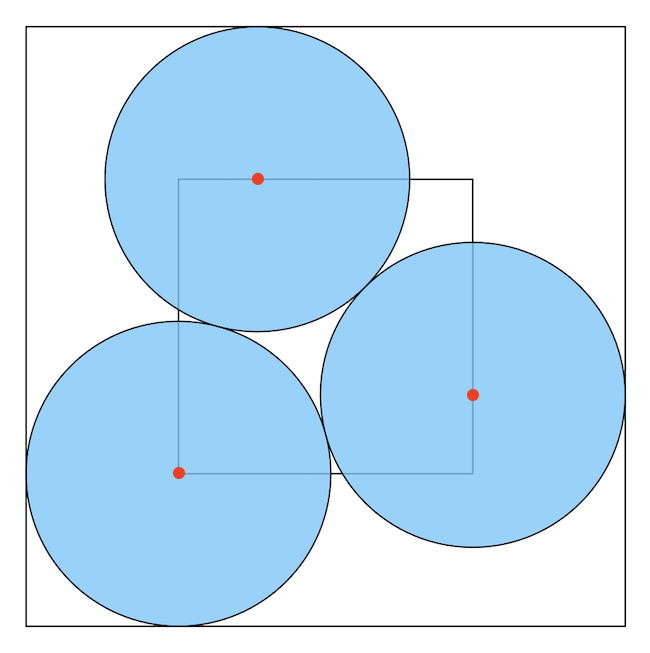
A körpakolás problémája különböző alakzatokba, különös tekintettel négyzetbe, régi probléma, ami általánosan (akárhány körre) nem megoldott, de kevés számú körre ismertek a megoldások, így három kör esetére is megtaláljuk a megoldást a Wikipédián. A fenti ábrát is innen vettük, és láthatjuk rajta, hogy az optimális elrendezés az, ha az egyik kör a külső négyzet sarkában van, a másik két kör pedig az említett sarokból induló átlóra szimmetrikusan helyezkedik el. A Wikipédia-szócikkben lévő listából kiolvashatjuk, hogy n = 3 darab egység sugarú kör pakolása esetén a legkisebb bennfoglaló négyzet oldalhossza kb. 3,931. A mi köreink azonban nagyobbak, esetünkben 2,5-el szorozni kell, így kapjuk, hogy a külső négyzet oldalhossza 9,8275, méterben számolva. Így a belső négyzetnek, azaz a szobának az oldalhossza 4,8275 méter lesz, tehát egy 23,3 négyzetméter területű négyzet alakú szoba fog megfelelni a feladat feltételeinek.

Ha azt szeretnénk, hogy bármelyik ember ki tudjon menni úgy a szobából, hogy közben végig betartja a minimális 5 méteres távolságot a többiektől, akkor viszont ennél nagyobb szoba kell. Egy 10 méter átlójú négyzet alakú szobában ez megvalósítható, ha a három ember három sarokban ül, az ajtó pedig a negyedik sarok közelében van. Ekkor az ajtóval szomszédos sarkokban lévő emberek a fal mentén el tudnak jutni a kijáratig, míg a szemközti az átló mentén haladva tud kijutni.

Kapcsolódó cikk a Qubiten: