144. feladványunkban Anzselika azt javasolta Zseraldinának, hogy felváltva pakoljanak Black Ivory és Kopi luwak kávészemeket egy NxN-es négyzetrács celláiba, ahol N páros. Ha betelt a tábla, akkor megnézik minden oszlopban és minden sorban, hogy ki nyerte meg azt a sort vagy oszlopot, azaz kinek van benne több kávészeme. A játék egészének a nyertese pedig az, akinek a végén nagyobb lesz az összpontszáma. Igaz-e, hogy akárhogy is rakják le a kávészemeket, a végén biztosan döntetlen lesz?

Politikusoknak testhezálló feladat

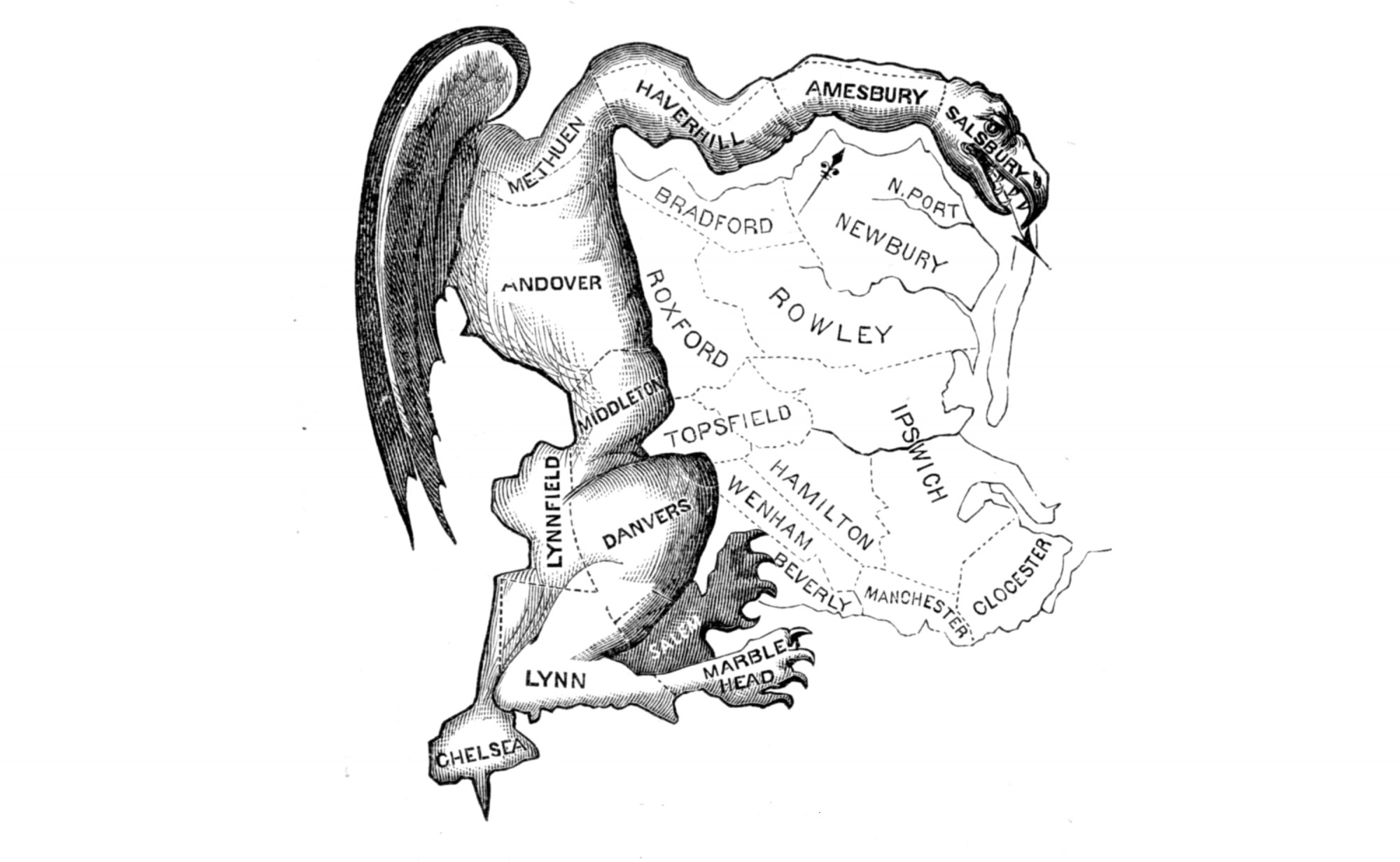
Konstruáljunk megoldást annak alapján, ahogy a politikusok manipulálják a választókerületeket annak érdekében, hogy az ő javukra dőljön el a választás. Ha két párt nagyjából azonos számú szavazatot szerezne egy választáson, nem különösebben nehéz úgy átrajzolni a választókerületeket, hogy az az egyik párt javára szolgáljon. Ez a választókerület-manipuláció, vagy angol eredetű kifejezéssel gerrymandering. A fogalom Elbridge Gerry (1744–1814) massachusetti kormányzóhoz kötődik, akinek nevéhez a salamander szó végét illesztették, mert 1812-ben aláírta azt a törvényt, amivel egy a legendabeli szalamandrára emlékeztető, fura alakú választókerületet hoztak létre, hogy megnehezítsék ellenfeleik dolgát.

Nézzünk ilyen manipulációra egy egyszerű példát: a Black Ivory és Kopi luwak pártokra leadott szavazatokat jelüljük B-vel és K-val. Legyen csupán 16 választópolgárunk, akik fele az egyik, fele a másik pártra szavaz. Ha a polgárokat a sorok mentén osztanánk csoportokra (választókerületekre), akkor a választás döntetlennel zárulna, mert az első két sor nyertese a Kopi luwak párt lenne, a második két sor nyertese a Black Ivory párt. Ha viszont oszlopok mentén határoznánk meg a választókerületeket, akkor az első oszlopban döntetlen alakulna ki, a következő kettőt megnyerné a Kopi luwak párt, és a Black Ivory párt pedig csak az utolsó oszlopot tudná elvinni. A példát természetesen fel lehet skálázni sok választópolgárra, sok választókerületre, és drasztikusabb különbséget is elő lehet állítani.

K K K B
K K K B
B B K B
B K B B

Láthatjuk, hogy a fenti példa az Anzselika és Zseraldina által játszott játékra is ad egy olyan megoldást, ami nem döntetlennel végződik, hiszen ha csak a sorokat értékelnénk, akkor döntetlen lenne, de az oszlopokat is hozzávéve a Kopi luwak kávészemek nyernek. Persze olyan példát is lehet hozni, hogy mindkét fajta kávészemből ugyanannyi van, mégis a Kopi luwak kávészemek nyernek mind a sorokra mind pedig az oszlopokra külön-külön, így tehát még drasztikusabb az eltérés a döntetlentől, lásd például alább.

K K K B
K K K B
K K B B
B B B B

Kapcsolódó cikk a Qubiten: