Magyar fizikusok kiszámolták a Laposföld gravitációs terét, és kiderült, hogy nem szeretnénk ott élni
„Kiszámoltuk Laposföld gravitációs terét, és ez alapján megállapíthatjuk, hogy Laposföldön valóban furcsa az élet” – írta Cserti József és Dávid Gyula a Fizikai Szemle 2022. augusztusi számában közzétett, Élet a Laposföldön című tanulmányban. Cserti, aki az ELTE Komplex Rendszerek Fizikája Tanszékének professzora, április végén mutatta be a különös kutatás eredményeit a kettejük által szervezett előadás-sorozat, az Atomoktól a csillagokig (AtomCsill) eseményén, az ELTE TTK Eötvös termében.
Az ismeretterjesztés trükkjeit láthatóan kisujjból kirázó Csertiéknek már a témaválasztásuk is ügyes volt: a belépő szintű összeesküvés-elméletek közé tartozó laposföld-hiedelemmel könnyű felkelteni a szélesebb közönség figyelmét, mert hát minek is foglalkoznak ilyen képtelenségekkel komoly fizikusok, miközben az elmélet boncolgatása kiváló alkalmat nyújt az olyan fizikai jelenségek valóságtól elrugaszkodott vizsgálatára, mint például a gravitáció.
De azért nem csodálkozunk, hogy a már önmagában is izgalmas Szemle-cikkben előre mentegetőznek a szerzők:
„Az »elmélet« számtalan más égbekiáltó, a mindennapi tapasztalatnak ellentmondó részletét mellőzve (például hová bújik éjjel a Laposföld síkja fölött mozgó Nap? – ezt a hívek további, egyre vadabb fantazmagóriákkal próbálják »magyarázni«) most csak ezzel a fentebb már említett, a laposföldhívõk által természetesnek tekintett elképzeléssel foglalkozunk: vajon milyen lenne a valóságban egy ilyen lapos korong vagy téglatest gravitációs tere? Tényleg úgy lehetne korzózni rajta, ahogy a városok sík főterén, úgy lehetne szelni hajónkkal a tükörsima vízszintes tengereket, ahogy a laposföldhívők mesélik, és a hajóból erős távcsővel előre nézve az egész úton látni lehetne a túlsó partot?”
A helyes válaszokat sejthetjük.
De mielőtt rátérnénk a Laposföld leírására, nem árt tudni, honnan vesszük azt, hogy a bolygónk valójában gömbölyű – mármint persze geoid, de ne finomkodjunk, ez nem földtanóra. Mint minden jó sztori, ez is az ókori görögökkel kezdődik.
Három évszázaddal azután, hogy Püthagorasz (diákoknak és matektankönyv-szerkesztőknek: Pitagorasz) sejteni kezdte a Föld gömbölyödését, Eratoszthenész (aki civilben az alexandriai könyvtár igazatója is volt) az i. e. 3. században elvégezte az első kísérleti méréseket a gömb alakú Föld elméletének bizonyítására. Ebben gátőrök és hivatásos lépésszámlálók munkája segítette a polihisztort. Előbbiek vették észre, hogy a nyári napforduló idején délben a Nílus vízállásmérő kútjának fenekét is elérik a nap sugarai Szüéné városában, vagyis a Ráktérítőre merőlegesen esnek. Eratoszthenész pontosan egy évvel később elutazott Alexandriába, hogy megnézze, ott milyen szögben esnek be a sugarak, majd a két város közötti távolság alapján kiszámította az adott szakasz görbületét. Google Térkép híján ehhez a vándorló lépésszámlálók munkájára volt szükség, akik mai szemmel meglepően pontosan jegyezték fel bizonyos városok egymástól való távolságát, így a Szüéné–Alexandria közöttit is – erre persze nem puszta kíváncsiságból bízták meg őket, hanem elsősorban mezőgazdasági és adózási célzattal. Eratoszthenész aztán ebből ki tudta számolni a Föld teljes kerületét, amennyiben az gömb alakú – mivel az, a számítása mindössze 1-2 százalékkal tért el a valóságtól.
De, mint minden jó sztori, ez is gyorsan túllendül az ókori görögökön. Ebben az esetben egészen a 17. századig ugrunk, Newtonig és az almafájáig, Csertiék ugyanis abból a jóhiszemű felállásból indultak ki, hogy a laposföldesek bedőlnek olyan hókuszpókuszoknak, mint a gravitációelmélet. Isaac Newton tömegvonzási törvényéből nemcsak az következtethető, hogy a bolygók a Nap körül keringenek, hanem az is, hogy a Föld magja nagy tömegének és sűrűségének köszönhetően sugárirányban vonzza magához a testeket. Emiatt lehetséges, hogy bárhol járunk a bolygó felszínén, a Föld magjától való közel azonos távolság miatt nagyjából ugyanakkora lesz az emberekre ható gravitációs erő, ami olyan hatást kelt, mint ha lapos földön sétálnánk.
Ha ezt elfogadjuk, olyan gondolatkísérletekbe lehet bocsátkozni, mint amilyet Cserti is említ: mi történne, ha fúrnánk egy lyukat a Föld magján keresztül, és elindulnánk benne autóval? Ha a hőmérsékleti vagy nyomási problémákat és más fizikai apróságokat figyelmen kívül hagyunk, és csak a gravitáció felől közelítünk, akkor az történne, hogy az autó a gravitációs erő növekedésével egyre nagyobb sebességgel gyorsulna a Föld középpontja felé, de amint több tízezer km/h-s sebességgel átszáguldanánk a magon, már lassulni kezdene, és mielőtt elérnénk a bolygóba vájt alagút másik végét, a gravitáció visszarántana, és harmonikus rezgőmozgásban mozognánk a lyukban oda-vissza a végtelenségig.
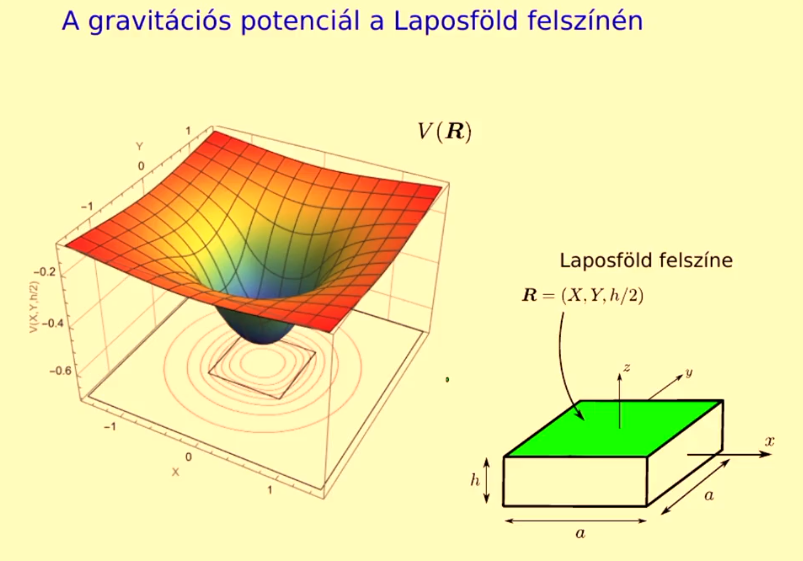
Na, de ha egy gömb gravitációs terét (illetve a mező adott pontjában érvényes gravitációs potenciált) ilyen szépen ki lehet számolni, akkor meg lehet-e ezt tenni egy téglatest esetében is? Már ha legalább annyit feltételezünk, hogy a Laposföld is háromdimenziós. A fizika és a matematika szépsége, hogy igen, ezt is ki lehet számolni, még ha integrálni is kell hozzá egy keveset – ebbe már Cserti sem akart nagyon belemenni, de azért megmutatta, milyen képletre kell gondolni:
Mármint, hogy innen lehet elindulni a számolgatásban, a 48 tagú teljes képlet valahogy így néz ki:
Ez ma már egyszerűen betáplálható egy tudományos számológépbe, úgyhogy nincs mentség, megvan a Laposföld (jó, egy tetszőleges téglatest) gravitációs potenciálja. Ebből kiderül, hogy a gravitációs térerősség a lapos bolygó középpontja felé húz, onnan távolodva lassan csökken, amiből az is következik, hogy mivel a gravitáció nem merőlegesen hat a felszínre, minél messzebb járunk a középponttól, annál jobban meg kell döntenünk a testünket, hogy ne essünk el. Így hiába sík a vidék, ahogy sétálunk a bolygó pereme felé, egyre inkább úgy érezhetjük magunkat, mint ha hegyet másznánk – ekkor ugyanúgy arra késztet a gravitáció, hogy a felszínre merőleges egyeneshez képest döntött szögben közlekedjünk.
Csertiék azt is kiszámolták, hogy egy 10 000 kilométeres oldalú négyzetre alapuló, 2000 kilométer magas és a Földével azonos sűrűségű Laposföld peremén annak a teste, aki megpróbál megállni a lábán, a talajjal 32 fokos szöget zár be, vagyis úgy érzi magát, mint egy 58 fokos meredekségű hegy oldalában. A sarkokon ez még tovább súlyosbodik: itt egy 67 fokos meredekségű hegy megmászásához lehet hasonlítani a talpon maradás kihívásait. De ez azt is jelentené, hogy például a fák is ferdén állnának a talajon a bolygó külsőbb régióin, és a pisai torony sem számítani különleges látványosságnak.
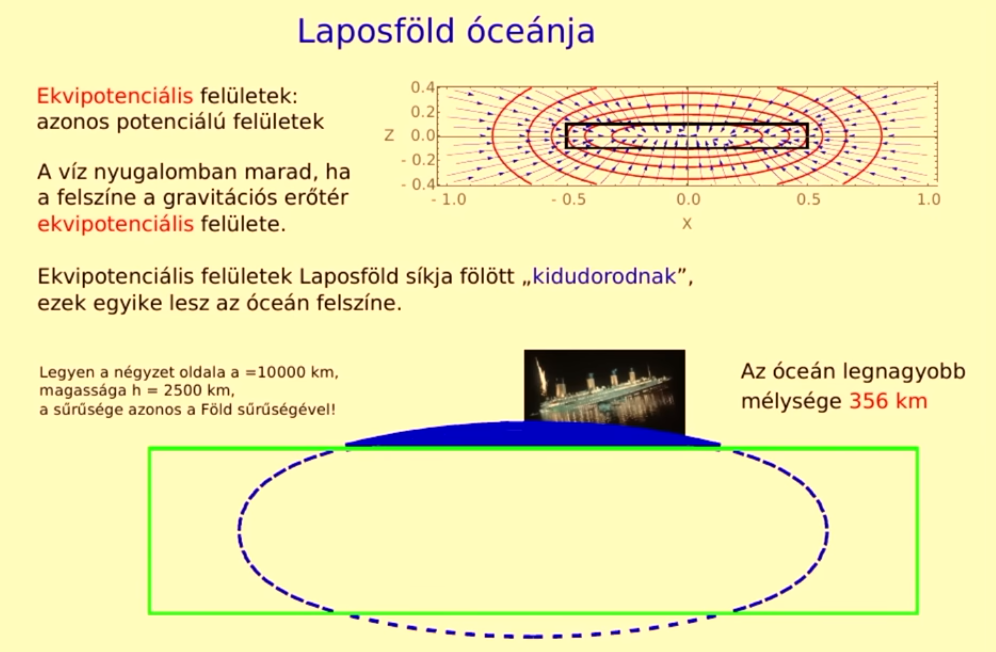
Bár a Laposföld egyik vonzereje lehetne, hogy békésen csónakázhatnánk az óceán tükörsima vízfelszínén, a valóság (bármennyire is erős a szóhasználat ebben a kontextusban) ki kell, hogy ábrándítson. Mivel a gravitációs erő hatása a lapos felszínen nem azonos minden egyes ponton, hanem az adott pont magassága mellett a középponttól való távolságtól is függ, a laposföldi óceán víztömegei az ekvipotenciális (azonos gravitációs potenciállal rendelkező) felületek mentén különböző magasságban helyezkednének el. Mivel a bolygó közepén a legnagyobb a gravitációs potenciál, az óceán víztömege is a középpont felé áramlik, így ott nagyobb magasságban gyűlik össze. Ez azt jelenti, hogy míg a gömb alakú Föld tengerei a szilárd kéreg homorulatait töltik ki vízzel, Laposföld óceánja a ferdén ható gravitációs erő miatt csepp formában dudorodna ki a felszínről.
Ha egy 10 000 kilométer oldalhosszúságú négyzetet veszünk a Laposföld alapjának, amit 2500 kilométeres magassággal és a Földével azonos sűrűséggel toldjuk meg, és a felszín felét kitevő óceánnal számolunk, a furcsa gravitációs hatás miatt egy 356 kilométer mély, a földfelszín fölé tornyosuló óceánt kapunk, ami egészen más élményeket ígér, mint a Földön megszokott, átlagosan 4 kilométer mély és a szemszögünkből sík tengerek.
És akkor arról még szót sem ejtettünk, hogy ha mindent középre húz a gravitációs tér, akkor ez a levegőre is igaz, vagyis a bolygó légköre a Laposföld középpontja környékén koncentrálódik. Így a perem irányába sétálni nemcsak a dőlés szöge miatt lesz olyan érzés, mint ha hegyet másznánk, de a levegő ritkulása is megnehezíti a dolgunkat.
Bár úgy tűnhet, hogy az ehhez hasonló számítások és gondolatkísérletek csak a fizikusok szórakoztatására valók, de a történelem azt mutatja, hogy a gravitáció vizsgálatának elméleti és gyakorlati haszna is felbecsülhetetlen, és ehhez még a Földet sem kell elhagyni. Amikor például Eötvös Loránd a 19. század végén kifejlesztette a torziós ingáját, még nem tudta, hogy néhány évtizeddel később az lesz a texasi és közel-keleti olajmező-feltárások legnépszerűbb műszere.
Cserti József alább megnézhető előadásából még részletesebben kiderül, milyen lenne az élet a Laposföldön, és miért örüljünk annak, hogy erről a gömb alakú Föld gravitációs kényelmében elmélkedhetünk.
Kapcsolódó cikkek a Qubiten: