A múltkor az entrópiával, a rendetlenség, kiszámíthatatlanság, szeszélyesség mértékével kezdtünk el foglalkozni. Most sem fogok belemenni a fogalom történetébe és leágazásaiba, most sem lesz ez fontos, csak megjegyzem, hogy a fizikából (a termodinamikából) származik, és ott is hasonló értelemben használják.

A fizikusok jól tudják, hogy ha egy fizikai rendszert magára hagyunk, annak nem fog csökkenni az entrópiája, vagyis rossz hírem van: ahogy mondani szokták, „A kakitündér nem létezik”, a rendetlenség magától nem csökken, annak ára van, azért tenni kell valamit. De én rendetlenség magától nem csökken, azért tenni kell valamit. De én továbbra sem az entrópia fizikai értelmezéséről fogok beszélni, hanem arról, amit mindenféle más tudományokban, például a nyelvészetben, nyelvtechnológiában használnak, szabályszerűségek, összefüggések feltárására, és hogy hogyan mérhetjük meg, mekkora az ára a rendetlenségnek, vagy ami ugyanaz: a rendrakásnak.

Említettem, hogy ha azt nézzük, hogy egy rendszernek maximálisan mennyi lehet az entrópiája, azzal tulajdonképpen a bonyolultságát tudjuk jellemezni. A legutóbbi teknősös példa nagyon egyszerű, kicsi a maximális entrópiája, mert csak azt néztük, hogy a teknősünk egy útkereszteződésben a négy út közül melyikeket szokta választani, ha sokszor elvégezzük a kísérletet. (Mivel sok kísérlet eredménye alapján próbáljuk jellemezni a teknőst, az entrópiának ezt az értelmezését statisztikainak szokták nevezni.)

A teknősnek csak négyféle viselkedését különböztetjük meg (Észak, Dél, Nyugat, Kelet), tehát a négyes szám jellemzi a rendszer bonyolultságát: ez a négy címke elég ahhoz, hogy minden egyes kísérletünk eredményét jellemezzük. Másképpen fogalmazva: minden egyes kísérletünkből csak annyit tudunk meg, hogy a négy irány közül melyiket választotta a teknőc. Ezért az entrópia tulajdonképpen az információmértékegysége is. Ha bonyolultabb lenne a kísérleti helyzetünk (ha nagyobb lenne a maximális entrópiája), akkor minden kísérletnek sokkal többféle kimenetele lehetne, több információt szereznénk belőle.

Ha a kísérleti helyzetünk még egyszerűbb lenne (mondjuk csak két irány közül választhatna a teknős), akkor kevesebb információt nyernénk egy-egy kísérlet elvégzéséből. Ha csak egy irányba tudna elindulni, akkor semmi információt nem kapnánk, 0 lenne a rendszer maximális entrópiája. De ugyanígy érdektelen lenne a teknősünk, ha a négy irány közül mindig ugyanarra indulna (mondjuk Délre, mint a múltkori görög teknős). A rendszer maximális entrópiája (bonyolultsága) nem lenne kisebb, csak a valóságosan mért entrópiája (a rendezetlensége) lenne 0.

Mennyi az annyi?

Hogyan jellemezhetjük a teknősös kísérlet bonyolultságát, maximális entrópiáját, ha négyféle irányba mehet? Más szóval: mennyi információt kapunk a teknőstől, amikor négy lehetőség közül egyet kiválaszt? Egyáltalán, miben mérjük ennek az információnak a mennyiségét? De hiszen erről már mindannyian hallottunk, mindenki tudja, hogy az információ mennyiségét miben mérjük: ugyanaz a mértékegysége, mint mondjuk egy számítógépes adathordozón (lemezen, pendrive-on stb.) tárolt adatmennyiségnek vagy szabad helynek, vagyis a bit, byte, megabyte, gigabyte stb. Ezeknek az alapegysége a bit, vagyis annyi információ, amennyit egy eldöntendő kérdésre kaphatunk válaszként (igen vagy nem, vagyis pont két lehetőség). Tehát ha a teknősünk csak két út közül választhatna, annak a rendszernek pontosan 1 bit lenne a maximális entrópiája, a bonyolultsága.

Ha a teknős négy irány közül választhat, akkor minden egyes választásából 2 bit információt nyerhetünk, mert ha ki kell találnunk, hogy 4 lehetőség (Észak, Dél, Nyugat, Kelet) közül melyiket választotta, akkor 2 igen/nem kérdésre van szükségünk (tessék utánaszámolni, hogy ez így van!). És most nem megyünk végig azon, hogy általában hány kérdésre van szükség, hanem elárulom, de minden olvasó utánaszámolhat, hogy ha n lehetőségünk van, akkor log₂n eldöntendő kérdéssel mindig megtudhatjuk, hogy az n lehetőség közül melyiket választotta a teknős. Például ha egy karakter (betű, számjegy stb.) tárolására 8 bit = 1 byte helyet fordítunk, vagyis log₂n = 8, akkor így n = 2⁸ = 256 karaktert tudunk megkülönböztetni. Röviden: az információ a lehetőségek számának logaritmusa.

Hogyan és mennyit tudunk spórolni?

De egyáltalán nem biztos, hogy minden karakter tárolására ugyanannyi helyet kell fordítanunk. El lehet képzelni olyan kódolást is, amiben bizonyos karakterek 8 bitnél rövidebb, mások 8 bitnél hosszabb helyet foglalnak el. És ennek gyakorlati értelme is lehet. Gondoljunk csak bele: ha egy hálózaton karaktereket akarunk továbbítani, és a hálózati szolgáltatónk bitenként kér érte valamennyi pénzt (miért ne kérne), akkor jó lenne, ha a gyakoribb karakterekre rövidebb kódot használnánk, mint a ritkábbakra. Könnyű belátni, hogy így tudunk a legtöbbet spórolni. Ezt persze csak akkor tudjuk megtenni, ha az egyes karakterek nem egyformán gyakoriak, vagyis ha az üzeneteinknek nem maximális az entrópiája. (Azt már láttuk, hogy akkor a legnagyobb az entrópia, ha minden lehetőség egyformán gyakori, például ha a teknőc minden égtájat egyforma gyakorisággal választ ki.)

Ezen alapulnak egyébként azok a tömörítő programok, amiket mindannyian használunk. Ha az adatainknak nem maximális az entrópiája, akkor a tömörítő eljárások gyakoribb és ritkább részeket tudnak bennük felfedezni, és a gyakoribbakat rövidebb, a ritkábbakat hosszabb adatokkal kódolják.

Pontosan hogyan, mennyit tudunk spórolni a karakterek továbbításánál? Ha csak az egyes karakterek gyakoriságát használjuk ki, akkor egyszerű a válasz. (A tömörítő eljárások ennél bonyolultabb szabályszerűségeket tudnak felfedezni.) Ha nem ragaszkodunk ahhoz, hogy minden karakter elküldéséhez pontosan 8 bitet használjunk (sőt, mivel elvontan beszélünk a problémáról, akár tört biteket is használhatunk), akkor úgy fogalmazhatunk, hogy minden egyes karakterre alkalmazhatjuk az információ fenti meghatározását: a választási lehetőségek számának logaritmusával számolhatunk. Ha minden karakter egyformán gyakori, akkor egy-egy karakter választási lehetősége éppen 256, abban az értelemben, hogy ha véletlenül kiválasztunk egy karaktert, akkor nagy átlagban 256-szor kell választanunk, hogy egy bizonyos karakter kijöjjön. De ha mondjuk a szövegünkben csupa négybetűs szó van, vagyis minden ötödik karakter a szóköz (space), akkor nagy átlagban csak 256/5-ször, vagyis 51,2-ször kell véletlenül választanunk, hogy a szóközt kapjuk meg. Ezért az ilyen szövegekben a space által hordozott információ csak log₂51,2 ≈ 5,7 bit.

A teknős maximális entrópiája: 2 bit

Akkor most már tudjuk, hogy az eredeti teknősös kísérletünk bonyolultsága, vagyis maximális entrópiája 2 bit. De azt még nem tudjuk, hogy hogyan becsülhetjük meg a teknősünk viselkedésének az összevisszaságát, entrópiáját. Csak azt tudjuk, hogy az maximum 2 bit lesz (ha teljesen össze-vissza választ, mindegyik irányt egyforma gyakorisággal), és minimum 0 bit, ha mindig ugyanarra indul, mintha számára csak egyetlen irány létezne (és azt láttuk, hogy akkor az egész rendszer bonyolultsága 0 bit lenne).

Mivel statisztikai jellegű rendszerünk van (sok kísérlet alapján próbáljuk jellemezni a teknős választásának egysíkúságát vagy szeszélyességét), nyilván csak becslésről beszélhetünk, és minél több kísérletet végzünk el, annál pontosabb lesz a becslésünk. De most tekintsünk el a pontatlanságtól, vegyük úgy, hogy nagyon sok kísérletet végeztünk el, elég sokat ahhoz, hogy ítéletet alkossunk a teknősünk viselkedésének összevisszaságáról, entrópiájáról. Ahogy a statisztikában általában szoktuk, a sok-sok kísérlet alapján azt feltételezzük, hogy a teknős átlagos viselkedése jó becslést ad. Vagyis a teknősös kísérletsorozatunk entrópiáját egy átlaggal fogjuk jellemezni: azzal, hogy átlagosan mennyi információt nyertünk egy-egy kísérletből. Tulajdonképpen ez az a képlet, amit keresünk, az entrópia mértékének képlete.

Ezt az átlagolást a fentiek alapján most már könnyűszerrel el tudjuk végezni. Tegyük fel, hogy minden teknősünkkel 100 kísérletet végzünk. Vegyük a teljesen kiszámíthatatlan teknőst, azt, amelyik Észak (é), Dél (d), Nyugat (ny) és Kelet (k) felé egyaránt 25-ször indul el. Akkor minden kísérletünk kimenetelének a sokfélesége 100/25 = 4, az általa hordozott információ log₂4 = 2 bit, és mivel mind a 100 kísérletben ezt a 2 bit információt kapjuk, az átlag is 2 bit lesz. Mint tudjuk, ez egyben a rendszer maximális entrópiája is. Ha azt a teknőst vesszük, amelyik mindig Délnek megy, akkor é = ny = k = 0, ezeknél 0 a választási lehetőség, és bár a 0 logaritmusa nem értelmes, ezek a kimenetelek nem hordoznak információt (úgy vehetjük, hogy ezek az irányok nem is részei a rendszernek). Viszont d = 100, aminek a sokfélesége természetesen 100/100 = 1, vagyis minden kísérlet log₂1 = 0 bit információt hordoz, és ezeknek az átlaga is 0. Ennyi, vagyis minimális a rendszer entrópiája.

Akik élnek, azok Délnek mennek

És akkor utoljára vegyünk egy olyan teknőst, amelyik inkább csak Észak és Dél felé szeret menni, de ezekbe az irányokba nagyjából egyforma gyakran. Mivel ez nagyjából olyan, mintha csak két irány közül választana, de a kettőt egyforma sokszor, azt várjuk, hogy 1 bit körül lesz az entrópia. Vegyünk konkrét számokat: é = 50, d = 44, ny = 3 és k = 3. Akkor a sokféleségek 100/50 = 2, 100/44 ≈ 2,3, és kétszer 100/3 ≈ 33,3, ezek logaritmusa log₂2 = 1, log₂2,3 ≈ 1,2, log₂33,3 ≈ 5,1. Az egyes kísérletekben szerzett információ átlagát így kapjuk meg:

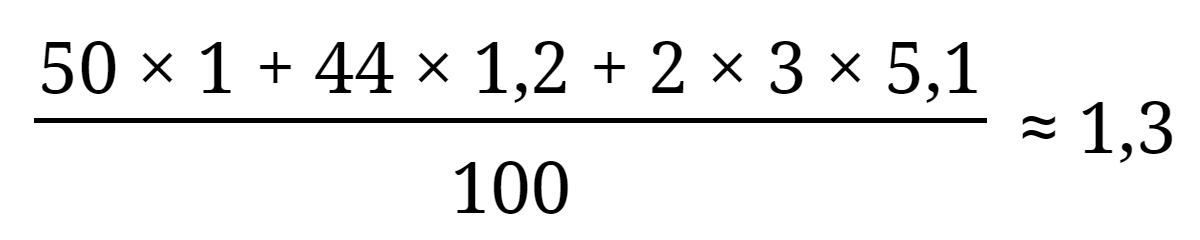
És akkor még pár szót arról, hogy mire jó ez az egész. Talán a leggyakoribb alkalmazása a (rész)rendszerek közötti összefüggések vizsgálata. A módszer pofonegyszerű: megmérjük két (rész)rendszer entrópiáját, összeadjuk a két összevisszaság mértékét, majd megnézzük, hogy ha egyetlen rendszernek tekintenénk őket, akkor kisebb rendetlenséget kapunk-e. Ha egyetlen rendszernek tekintve jóval kisebb az összevisszaság, mint a két külön-külön vett entrópia összege, akkor könnyen lehet, hogy a két rendszer összefügg egymással. (Pontosabban: csak akkor lehet, hogy összefüggnek egymással.)

Vegyük például az előző teknősünket: össze-vissza indul Észak meg Dél felé, de Kelet meg Nyugat felé nem nagyon megy, a 100-as kísérletsorozatunk entrópiája 1,3. És legyen a másik rendszer az időjárás változása valamilyen egyszerű értelemben, például úgy, hogy csak azt nézzük, hogy melegszik-e a levegő, vagy hűl (ez két lehetőség, tehát 1 bit). Tegyük fel, hogy majdnem ugyanannyiszor melegszik (mondjuk 53-szor), mint amilyen gyakran hűl (mondjuk 47-szer), vagyis az entrópia gyakorlatilag a maximális 1 bit. Ha valamilyen összefüggés van a két rendszer között, például a teknősünk inkább Dél felé megy, ha hűl az idő, viszont inkább Észak felé akkor, ha melegszik, akkor a két rendszert egynek tekintve jóval kisebb entrópiát kell kapnunk, mint 1,3 bit +1 bit = 2,3 bit.

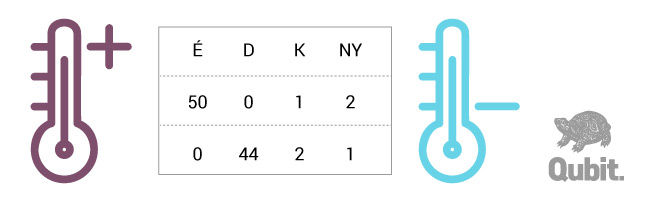
Ezt is könnyen kiszámíthatjuk. Ha egyetlen rendszernek vesszük a kettőt, és mind a 100 kísérletben feljegyezzük a választott égtáj mellett a hőmérséklet változását is, akkor nyolcféle kimenetel lehetséges, vagyis a maximális entrópia log₂8 = 3 bit, vagyis a két rendszer maximális entrópiájának összege (2 bit + 1 bit). Ha a teknősünk tényleg szigorúan a hőmérséklet-változás szerint választ, akkor mind az 50 esetben, amikor Északra indul, akkor melegszik az idő (m), és mind a 44 esetben, amikor Dél felé, akkor hűl (h). (A maradék 6 esetben valahogy össze-vissza változik a hőmérséklet.) Tehát ilyesmi eredményeket kapunk:

Olvasóink most már maguktól is ki tudják számolni ennek az összetettebb rendszernek az entrópiáját, én elárulom, hogy kb. 1,4 az eredmény. A két rendszer entrópiájának összegéhez, a 2,3-hoz képest tehát kb. 0,9 bit csökkenést tapasztaltunk, ez fejezi ki a lehetséges összefüggésük mértékét. Szakszóval ezt a két rendszer kölcsönös információjának nevezzük.

Most már csak az a kérdés, hogy mennyire jelentős (szakszóval: szignifikáns) ez a csökkenés. Persze látjuk, hogy jelentős, hiszen a 0,9 bit majdnem annyi, mint az egyik rendszer (az időjárás) teljes entrópiája. A jelentőségét számszerűsíteni is lehet, csak jó bonyolult a matematikája, ezért itt nem fogok róla beszélni. Mindenesetre én kiszámoltam, 0,006 a szignifikancia-szintje, ami azt jelenti, hogy csak nagyon ritkán, 1000 véletlen próbálkozásból átlagosan hatszor fordul elő ilyen (vagy ennél nagyobb) egybeesés. De véssük az eszünkbe: ez nem azt jelenti, hogy az összefüggés nem a véletlen műve, csak azt, hogy a hasonló bonyolultságú rendszerek együtt szemlélése igen ritkán vezet ilyen nagy (vagy még ennél is nagyobb) fokú entrópia-csökkenéshez.