Galaktikus genderkérdés című feladványunkban egy háromnemű idegen faj populációjában beálló nemi egyensúlyt kellett meghatározni. A feladat szerint a faj egyedei nemüket tekintve háromfélék lehetnek, amiket két nemi kromoszómájuk határoz meg. Az XX kromoszómapárral rendelkezők az alfák, az YY kromoszómapárral rendelkezők a béták, a vegyes XY kromoszómapárosok pedig a gammák.

Bármely két különböző nemnek lehet utódja, és a szülők a kromoszómáik közül az egyiket örökítik tovább. Ennek megfelelően egy alfának (XX) és egy bétának (YY) mindig gamma lesz az utódja. Egy gamma (XY) és egy alfa (XX) utódjának a nemét az dönti el, hogy a gamma szülő melyik kromoszómáját örökíti tovább. Az esetek felében az X-et, és ekkor alfa lesz az utód, az esetek másik felében Y-t, és ekkor gamma lesz az utód. Béta (YY) és gamma (XY) szülők esetén ugyancsak a gamma átörökített kromoszómája fog dönteni, és az utód itt is 50-50 százalék eséllyel örökli valamelyik szülője nemét.

Most nézzük, milyen valószínűséggel kerülnek össze különféle nemű szülők. Legyen az alfák, béták és gammák száma a populációban rendre, A, B és C. Képzeljünk el egy hatalmas gráfot, amiben minden pont egy egyednek felel meg. Kössük össze (ún. élekkel) ebben a gráfban azokat a pontokat, amelyek potenciálisan szülőpárok lehetnek, azaz különböző neműek.

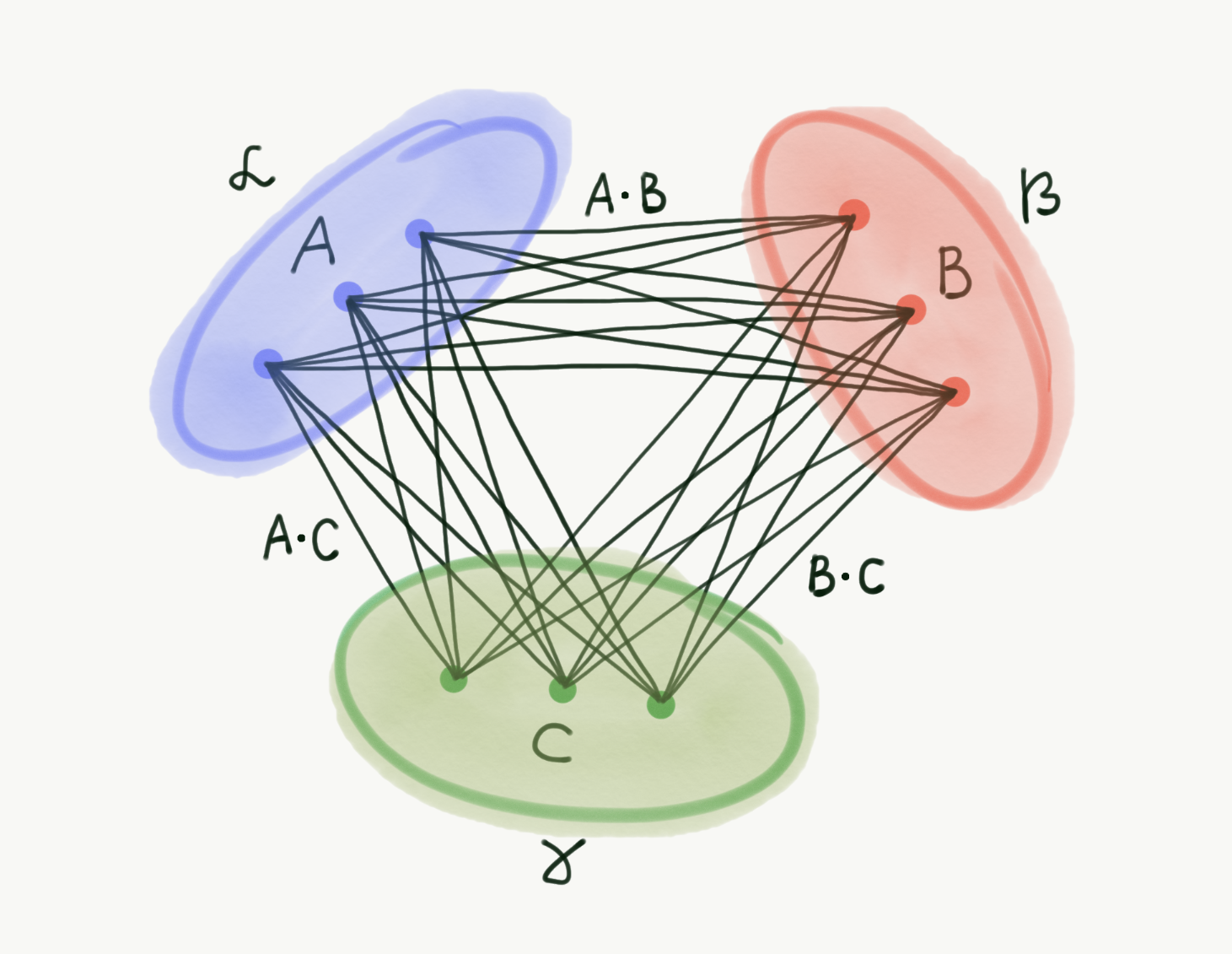
Ha például az a kérdés, hogy hány lehetséges alfa-béta szülőpár van, akkor az alfák és béták között menő éleket kell leszámolnunk. Mivel az A darab alfa pont mindegyikéből indul él a B darab béta pont mindegyikébe, ezért az alfák és béták között menő összes él száma A-nak és B-nek a szorzata lesz. Ha az a kérdés, hogy véletlenszerűen választva az összes lehetséges szülőpáros közül mekkora valószínűséggel választunk alfa–béta szülőpárost, akkor A·B-t le kell osztanunk az élek összes számával, azaz A·B + B·C + A·C értékkel. Ennek megfelelően a különféle fajta szülőpárok kiválasztásának vagy előfordulásának valószínűségei az alábbiak szerint alakulnak:

• alfa–béta előfordulási valószínűsége: A·B/(A·B+B·C+A·C)
• béta–gamma előfordulási valószínűsége: B·C/(A·B+B·C+A·C)
• gamma–alfa előfordulási valószínűsége: A·C/(A·B+B·C+A·C)

Mindebből kiindulva az egyes nemek születési valószínűségei az alábbiak szerint alakulnak:

• alfa születési valószínűsége: (1/2)·A·C/(A·B+B·C+A·C)
• béta születési valószínűsége: (1/2)·B·C/(A·B+B·C+A·C)
• gamma születési valószínűsége:
  (1/2)·A·C/(A·B+B·C+A·C) + (1/2)·B·C/(A·B+B·C+A·C) + A·B/(A·B+B·C+A·C)

Egyensúlyi állapotban ugyanezeknek a valószínűségeknek rendre a = A/(A+B+C), b = B/(A+B+C) és c = C/(A+B+C) értékeket kell felvenniük. Ezekből az alábbi egyenletrendszer adódik az így bevezetett a, b és c egyed-előfordulási valószínűségekre:

• 2·a = a·c/(a·b+b·c+a·c)
• 2·b = b·c/(a·b+b·c+a·c)
• 2·c = a·c/(a·b+b·c+a·c) + b·c/(a·b+b·c+a·c) + 2·a·b/(a·b+b·c+a·c)

Már a feladat elején megállapítható volt, és az egyenletekben is látjuk, hogy az alfák és béták szerepe teljesen szimmetrikus. Ennek megfelelően jogosnak tűnhet az érvelés, miszerint az arányuk is egyforma kell legyen, tehát egyszerűsítsük képleteinket azzal a feltevéssel, hogy a = b. Ebben a esetben, mivel a+b+c = 1, rögtön következik, hogy a = b = (1 - c)/2. Ezt az első egyenletbe helyettesítve némi algebra után kapjuk, hogy c^2 = 1/3, tehát c ≈ 0.577, és a = b ≈ 0.211.

A gondolatmenet azonban nem helyes! 

Igaz ugyan, hogy az időbeli változást leíró egyenletekben a és b felcserélhető, azonban ahhoz, hogy tudjuk, miként alakul időben egy folyamat, a dinamikát leíró egyenletek mellett a kezdőfeltételekre is szükség van. Ha a kezdőfeltételekben aszimmetria van, akkor szimmetrikus időfejlődési egyenletek mellett is lehet aszimmetrikus a későbbi állapot. Példaként vegyünk egy hegyére állított ceruzát. A ceruza számára minden irány egyenértékű, minden irányba ugyanúgy dőlne le a ceruza. Nagyon óvatosan talán megállíthatjuk a hegyén, de egy apró fuvallatra rögtön el fog dőlni, ezt hívjuk instabil egyensúlyi helyzetnek és szimmetriasértésnek a fizikában. A legkisebb véletlenszerű zaj hatására megbomlik a kezdeti szimmetria, és kiválasztódik egy ledőlési irány, amely korábban nem volt kitüntetett.

Esetünkben a feladat nem adta meg a kezdőfeltételeket, azaz a kezdeti populációban a nemek arányát. Vegyük például azt az extrém esetet, hogy az alfák vagy a béták nincsenek is, azaz valamelyiknek a számossága nulla, például valami vírus okozta kihalás miatt, ami csak az egyik nemet érintette. Nos, ebben az esetben, a maradék két nem közti egyensúly pont olyan lesz, mint férfiak és nők esetében, azaz fele-fele arányban fog beállni a maradék nemek aránya. Ez azonnal látható például b = 0 helyettesítéssel az első egyenlet alapján.

Általában pedig különböző kezdeti feltételek esetén különböző egyensúlyi arányok fognak beállni, tehát nincsen egyértelmű megoldása a feladatnak. Feltehető azonban a kérdés, hogy mennyire stabil a beállt egyensúly egy adott esetben. Tegyük fel, hogy nincsenek olyan nagy perturbáló hatások, mint mondjuk egy vírus okozta járvány, ami csak az egyik nemet érinti, de a folyamat véletlenszerűségéből adódó véletlenszerű ingadozások jelen vannak. Minél kisebb a populáció, annál nagyobb ingadozásokat tudnak okozni a nemek arányában a véletlenszerű elhalálozások és születések.

Az alábbi grafikonon egy tízezer fős populációt látunk, amit az a = b szimmetriamegfontolás alapján elméletileg számolt egyensúlyi állapotból indítottunk, de látható, hogy pusztán a véletlenszerű ingadozások révén a béták kihalnak, és csak alfák és gammák maradnak közel egyenlő arányban. Tehát az aszimmetriát, sőt akár egy nem teljes kihalását, nemcsak a kezdeti feltételek, de a véletlenszerűség is tudja okozni! 

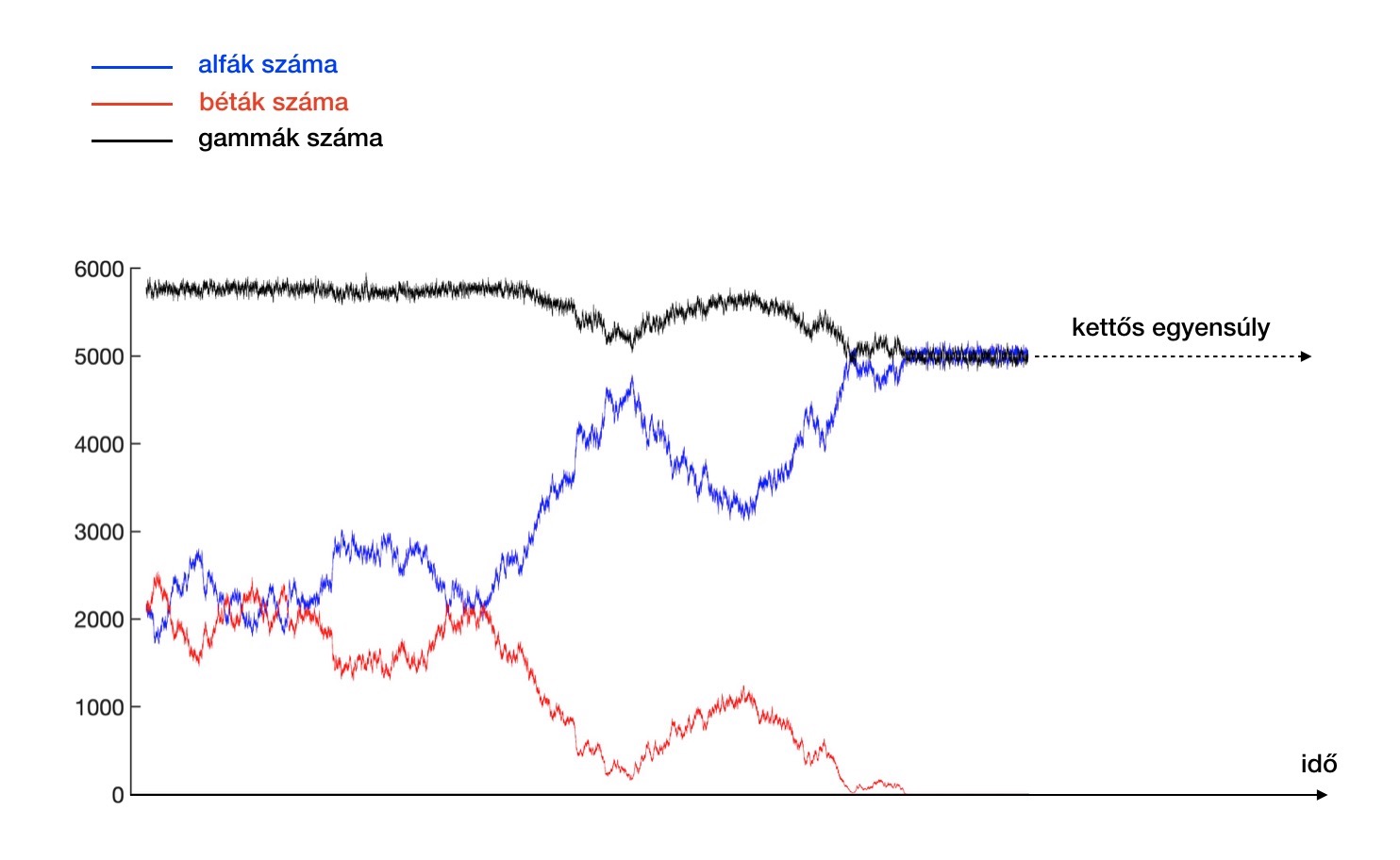
Azt is láthatjuk, hogy a három nemből álló rendszer sokkal instabilabb, mint a két nemből álló rendszer. Talán nem véletlen, hogy az állatvilágban is leginkább két nemet figyelhetünk meg. Feladatunk természetesen csak gondolatébresztő, amely rávilágít a probléma néhány aspektusára. A valóság ennél sokkal bonyolultabb is lehet genetikailag, és persze a párválasztás sem írható le olyan egyszerűen, mint ahogyan a feladatban modelleztük.