Milyen messze van a járvány csúcsa Magyarországon, és hogyan tudjuk ezt modellezni?

A járványdinamika alapjairól és a legegyszerűbb járványterjedési modellből – az ún. SIR modellből – levonható néhány nagyon fontos következtetésről Kun Ádám két korábbi cikkében már írt a Qubiten. Ezek a cikkek nemcsak a járvány lefolyásának érzékeltetését célozzák, hanem arra is kitérnek, hogy milyen egyéni cselekvéssel befolyásolhatjuk jelentősen a járványt, sőt feltétlenül szükséges is lenne befolyásolnunk, mert ennek hiányában határozottan súlyos kimenetelű lehet a hatása az egész társadalomra, különösen az idősekre nézve.
Megdöbbentőek az erősen fertőzött országokból érkező híradások, például az olasz állapotokról, ahol orvosoknak már tucatjával kell életekről dönteniük, és legutóbb csaknem 800 ember halt meg egy nap alatt. Idehaza azonban mindenki abban reménykedik, hogy ez velünk nem fordulhat elő. Ehhez viszont nem csak reménykedni kellene, hanem tenni is kell érte: nagyon fontos mindenkinek egytől-egyig komolyan venni a szakértők tanácsait már most, a járvány legelején.
Ebben a cikksorozatban a korábban bemutatott SIR modellnek a lappangási időt is figyelembe vevő, a valóságot valamivel jobban közelítő változatával, az ún. SEIR modellnek és variánsainak segítségével szeretnék még alaposabb betekintést nyújtani a járványdinamikába. Az elérhető adatok alapján futtatott szimulációk eredményeit felhasználva körbejárok néhány kifejezetten időszerű kérdést, ami remélhetőleg segít jobban érzékeltetni többek között azt is, hogy milyen komolyan kell vennünk a járványt, milyen lehet a lefolyása, és miként tudunk hatni a kimenetelre.
Előtte azonban foglaljuk össze Kun Ádám korábbi írásainak fontosabb megállapításait:
- A fertőzés kezdetben egyértelműen exponenciálisan növekszik, ami egy olyan gyors növekedés, amit a legtöbb ember nagyon nehezen tud elképzelni, és egyik pillanatról a másikra nagyságrendeket ugorhat a fertőzöttek száma.
- Mindenki fogékony a vírusra, nincs védőoltás, nincs gyógyszer, a lappangási időt nem tudjuk befolyásolni, a járvány terjedésével kapcsolatban ezért egyedül az emberek közti kontaktusok számára és az átadás valószínűségére van ráhatásunk, amit a SIR modellben a β paraméter foglal magába.
- Ezt az általunk egyedül kontrollálható β paramétert szigorú rendeletekkel és egyéni odafigyeléssel – társas érintkezéseink drasztikus csökkentésével és szigorú higiéniai szabályok betartásával – van csak módunk csökkenteni.
- Drasztikus korlátozó szabályok nélküli fertőzési rátával számolva, ha a β paramétert időben fixnek tekintjük, akkor egyszerű modellszámításokból az adódik, hogy a populációnak szinte az egésze (80-90 százaléka) átesik a víruson.
- Ráadásul, ha a β paramétert nem csökkentjük le jelentősen, akkor az egészségügyi rendszer a járvány csúcspontján, sőt már előtte is, nagy valószínűséggel hatalmas mértékben túlterhelődik.
- Ahhoz, hogy az egészségügyi rendszer ne terhelődjön túl, a β paramétert olyan mértékben kellene csökkenteni, hogy az egyúttal a járványnak sok hónapra, de akár évekre történő elhúzódását is jelentheti.
- A brit elképzelés: ha úgysem tudjuk eléggé ellaposítani a járványgörbét, és jelentős halálozási ráta csak az időseknél tapasztalható, akkor izoláljuk őket, és a lakosság többi részén menjen át a fertőzés gyorsan. Így a járvány végeztével a lakosság nagy része immunis lenne, és a későbbiekben a nyájimmunitás már megvédené az időseket is. A probléma csak az, hogy az idősek és az őket gondozók nagyon nagy százalékot tesznek ki az európai elöregedett társadalomban. További megjegyzés: mivel a SARS-CoV-2 új vírus, valójában nem tudjuk még, hogy mennyi időre szerez védettséget az, aki átesett a fertőzésen.
- A legjobb lehetőség a járvány megállítása lenne, ez azonban csak a betegek izolációjával lehetséges. Megjegyzés: ez a több napos lappangási idő és az országos elterjedség miatt nagyon nehéz feladat lenne.
- Akár elhúzni szeretnénk a járványt az egészségügyi rendszer terhelésének csökkentése érdekében, akár teljesen megállítani, mindkét esetben nagyon fontos előfeltétel a β paraméter, azaz találkozásaink számának a csökkentése. A vírushordozók izolációjához ugyanis kontaktkutatás is szükséges, ami sokkal könnyebb, ha eleve kevés a kontaktus.
Miért nagyon bizonytalanok a járvány csúcsának előrejelzései?
A továbbiakban a korábban már ismertetett SIR (susceptible, infected, recovered, vagyis fogékony, fertőzött, gyógyult) modell egy kiterjesztését fogjuk használni, az úgynevezett SEIR (susceptible, exposed, infected, recovered, tehát fogékony, látens, fertőzött, gyógyult) modellt.
A SIR modell azokra a vírusokra alkalmas leginkább, ahol a fertőzött egyén lényegében rögtön fertőzőképes. Ide tartozik például több influenzavírus, ami sokszor a fertőzéstől számítva néhány órán belül fertőzőképes. Az új koronavírus esetében azonban viszonylag hosszú a lappangási idő, átlagosan kb. 5 nap, ezért a SIR modellhez képest bevezetünk egy negyedik csoportot (E), és ezzel együtt a populációt minden időpillanatban az alábbi négy csoportra osztjuk:
- Susceptible (S): Fogékonyak csoportja, akik potenciálisan elkaphatják a fertőzést.
- Exposed (E): Olyan fertőzöttek csoportja, akikben lappang a betegség, de még nem fertőzőképesek.
- Infected (I): Olyan fertőzöttek csoportja, akik tovább tudnak fertőzni. Tipikusan tünetekkel rendelkeznek, bár ez is kérdéses, de ez most a modell szempontjából lényegtelen.
- Recovered (R): Gyógyultak csoportja, akikről ebben a modellben feltesszük, hogy rezisztensekké válnak, azaz nem tudnak újrafertőződni.
A továbbiakban a csoport jele egyúttal a csoport létszámát is fogja jelenteni, ezek lesznek a változó mennyiségeink. A populáció teljes számát N-el jelöljük, és ha a születésektől és halálozásoktól eltekintünk, akkor minden t időpillanatban teljesül, hogy N = S(t)+E(t)+I(t)+R(t) = N.
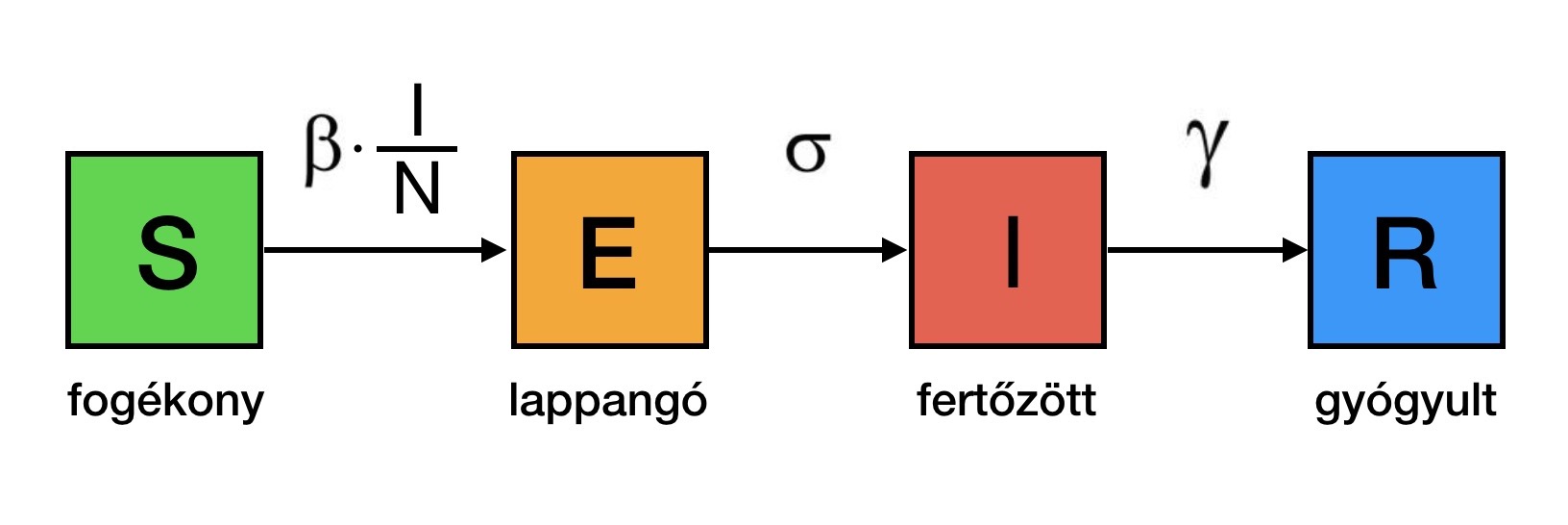
A fenti csoportok között az átjárás csak a nyilak irányába lehetséges, és minden átmenethez tartozik egy ráta, kiáramlási sebesség, ami egyúttal a szomszédos csoportba történő beáramlási sebesség is. Az egyes ráták reciprokai idő dimenziójú mennyiségek, és lényegében az egyes csoporton belül töltött átlagos időt adják meg, tehát például 1/σ az átlagos lappangási idő, (említettük már, hogy ezt 5 napnak vehetjük), 1/𝛾 pedig a fertőző állapotban töltött átlagos idő. Egyébként mindkét időtartamnak nagyon nagy a szórása.
Az emberek maguktól válnak lappangóból fertőzőképessé és abból gyógyulttá. Vagyis az E-ből I-be és I-ből R-be történő átáramlásokhoz fix ráták tartoznak. Ezzel szemben S-ből E-be fertőzési esemény váltja ki az átjutást, amihez egy fogékony és egy fertőző találkozására van szükség, ezért ez a ráta függ a találkozás valószínűségétől, ami arányos I/N-el. A ráta maradék része a korábban is már említett β paraméter, amit két faktor határoz meg az alábbi módon:
β = (kontaktusok időegységre vonatkoztatott száma) × (fertőzés átadásának valószínűsége)
Természetesen minden mennyiség alatt annak átlagos értékét értjük. A második zárójelben lévő tag pedig függ a vírus fertőzési mechanizmusától és az egyének higiéniás szokásaitól egyaránt.
Ezek után már – de csakis a műkedvelők kedvéért – könnyen felírhatjuk azokat a differenciálegyenleteket, amik leírják, hogyan változnak az egyes csoportok létszámai az időben:

A valóságban persze a járványterjedés véletlenszerű, úgynevezett sztochasztikus folyamat. A fenti folytonos SEIR modell akkor használható jól, ha jól kevert a populáció, és nagy a mérete, sőt az egyes csoportok létszáma is külön-külön nagy, hiszen az egyenletben valós számok szerepelnek, a valóságban viszont S, E, I és R értékei minden időpillanatban csak egész számok lehetnének. A különbség csak akkor lényegtelen, ha mindegyik szám nagy. A járványterjedési jelenségek legfőbb vonásait azonban akkor is mutatják ezek az egyenletek, ha a fenti változók értékei történetesen nem egész számok.
A fenti egyenletek megoldását, azaz változóink időbeli változását leíró S(t), E(t), I(t), R(t) függvényeket számítógépes szimulációval, de akár analitikusan is meg lehet adni. Ehhez viszont előbb meg kell adnunk a modell paramétereit (β, σ, 𝛾) és a kezdőfeltételeket, azaz változóink értékeit a kezdő időpontban: S(0), E(0), I(0), R(0).
Nézzük előbb a paramétereket. Elfogadható feltételezés, hogy σ és 𝛾 leginkább a betegségre jellemző állandók, amiket az eddigi mérések alapján a szakirodalomból vehetünk. Az egyszerűség kedvéért használjuk Röst Gergely járványmodellező kutatócsoportja által is használt adatokat (1/σ = 5.1 nap, 1/𝛾 = 3.3 nap), amiket abban a cikkben is használtak, amelyben még februárban előre megjósolták, hogy mely európai országokat veszélyezteti leginkább a Kínából kiszabaduló vírus.
Az előző két paraméterrel szemben β értékére lehet befolyásunk, és emiatt ez idővel is változhat. Az irodalomban β helyett sokszor az ún. R0 = β/𝛾 alap reprodukciós számot szokták közölni, ami megadja azt, hogy a fertőzőképesség ideje alatt átlagosan hány másik embert fertőz meg valaki. Ezt a számot Kínában 2 és 3 közöttinek mérték, a fenti cikkben kínai adatok alapján R0 = 2,6 átlagos értékkel számoltak. Egy tipikus influenza esetén például R0 = 1,3, de ahhoz, hogy R0 értékét ennyire letornázzuk, jelentős változásokat kellene eszközölnünk.
A másik fontos adat – ha jósolni szeretnénk –, hogy jelenleg hány fertőzött van. A kormányzati tájékoztatás szerint a regisztrált fertőzöttek száma március 24-én 187 volt, ennél azonban jóval többen lehetnek – több okból is, de leginkább azért, mert nem minden beteget regisztrálnak, hazánkban ráadásul rendkívül kevés tesztet végeznek. Nem tudjuk tehát, hogy hány beteg van valójában, de megfelelő szorzószámokat használva az 5000 elfogadható alsó becslésnek tűnik.
Ha 5000 fertőzöttel (plusz lappangók) és R0 = 2,6 reprodukciós számmal számolunk, akkor a SEIR modellszimulációk az alábbi eredményt adják egy akkora zárt populációra, mint a kb. 9,77 milliós magyar lakosság. SEIR modellt szimuláló grafikus programokat egyébként a weben is lehet találni, így bárki számára könnyen ellenőrizhető az alábbi ábra, de akár még ennél is több állítható paraméterrel lefuttatható a modell.
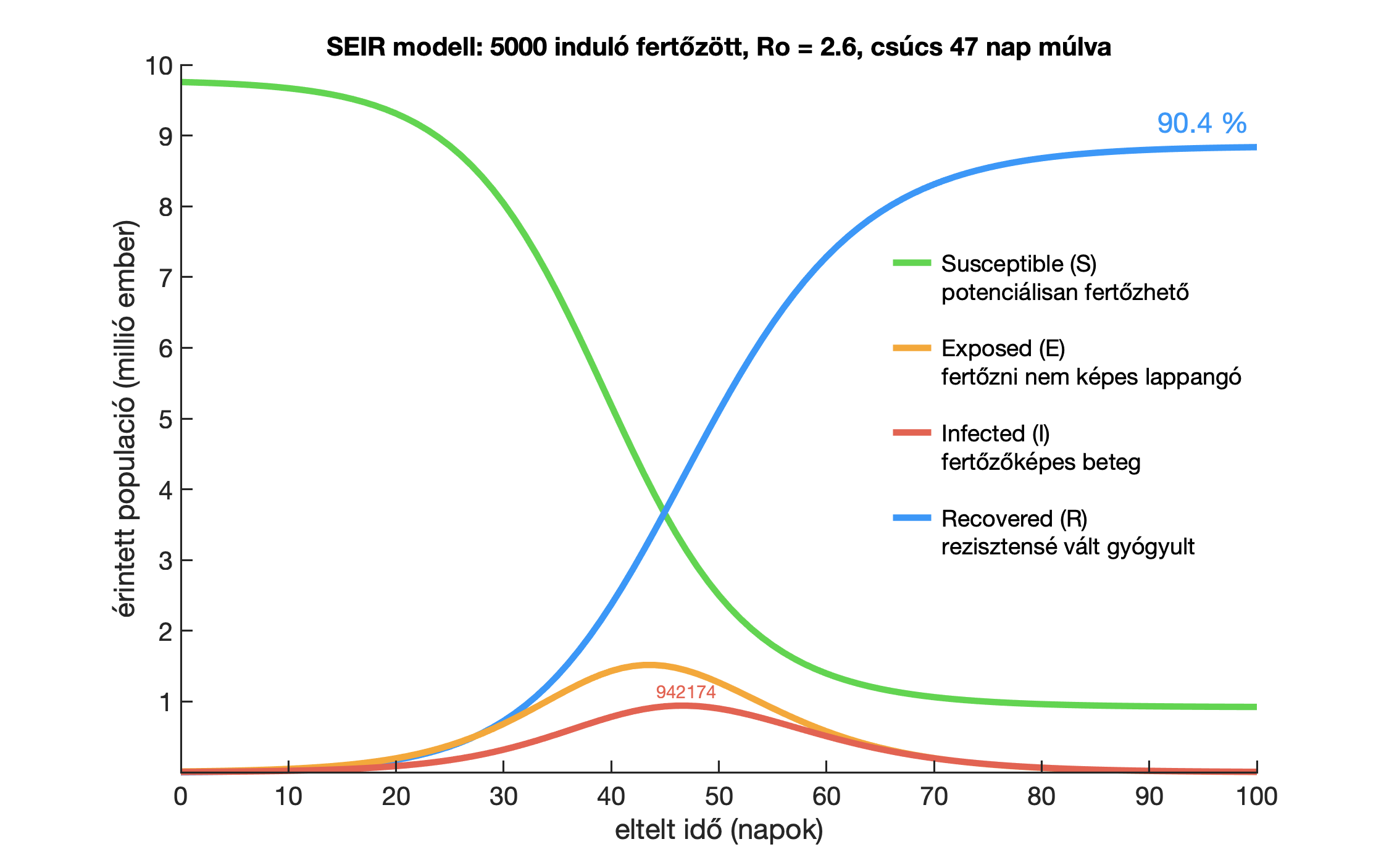
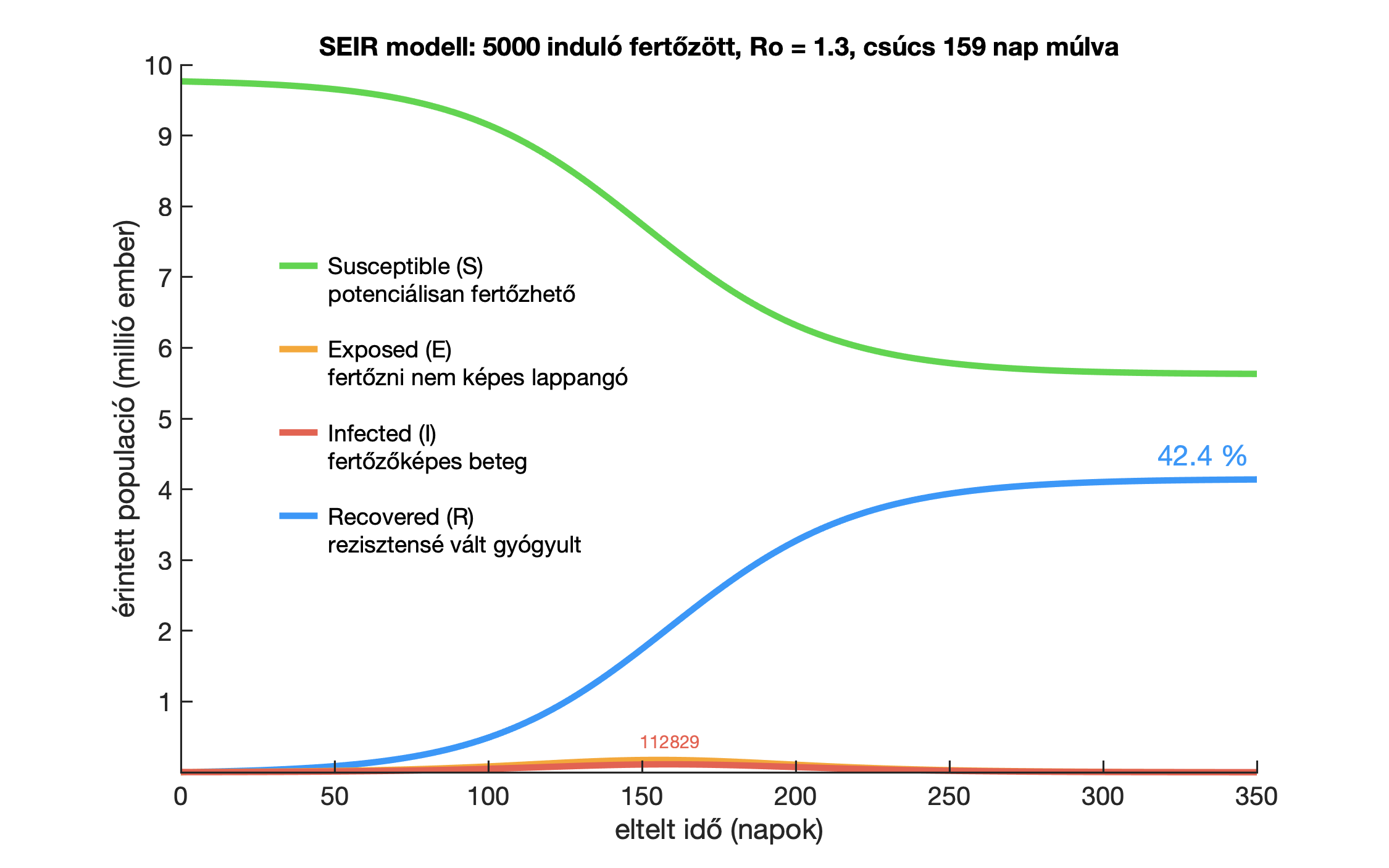
R0 = 2,6 esetén tehát 47 nap múlva várható járvány tetőzése a modell szerint. De mi van akkor, ha alacsonyabb R0-al számolunk? Például R0 = 2, vagy R0 = 1,3 esetén (influenzaszerű terjedés) az adódik, hogy a tetőzéstől rendre 64, illetve 159 napra vagyunk, az utóbbihoz tartozó ábrát lásd alább. Ezek nagyon jelentős különbségek. A fenti ábrához képest például két héttel tolódik ki a csúcs, ha R0 = 2 -vel számolunk. Az R0-t tehát szeretnénk minél jobban letornázni, és ez nem csak azért lehet fontos, hogy kevésbé terheljük a kórházi ellátást, de lenne még időnk felkészülni számos dologra, például elegendő számú védőmaszk beszerzésére és gyártására.
Mint említettük, a fertőzöttek valódi számának nem ismerete is jelentős bizonytalanságot tud okozni. Ha csak a cikk megjelenésének napjáig (március 24.) regisztrált és közölt 187 fertőzöttel számolnánk, akkor R0 = 2,6 esetén három héttel későbbi csúcsot kapnánk, amint azt az alábbi ábra mutatja.
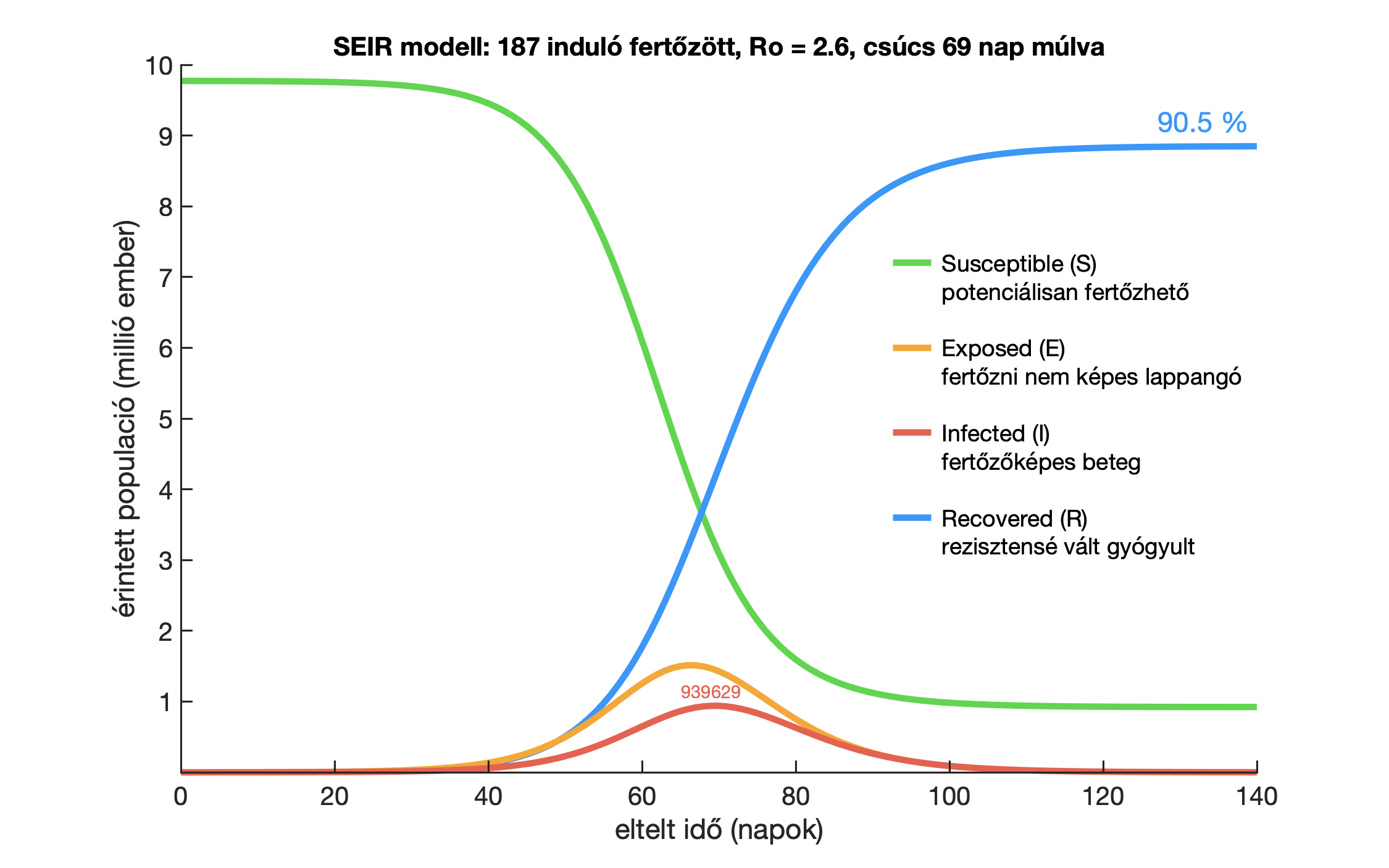
Látható tehát, hogy meglehetős a bizonytalanság a járvány tetőzésének időpontját illetően, és akkor még nem beszéltünk az egyéb paraméterek kiszámíthatatlanságáról és a véletlenszerűségből adódó zajról. A fertőzöttek száma a tetőzéskor viszont lényegében csak R0-tól függ, ezt mutatják a piros haranggörbék fölé írt számok. Aki további paraméter kombinációkra szeretné megtudni, hogy mit jósol a SEIR modell, az eredményeket megtekintheti itt a szerző blogján.
Fontos hangsúlyozni azonban, hogy a SEIR modell nyilvánvalóan nem írja le teljesen a valóságot, hiszen az sok ponton eltérhet a modelltől. Csak néhány ezek közül, amiket a modellben nem vettünk figyelembe:
- emberek klasztereződése háztartásokba;
- emberek kapcsolati hálója, akár életkor szerinti felbontásban;
- munkába járás, bevásárlás, orvoshoz járás speciális körülményei;
- fertőzőképesség nem egyenletes volta a betegség ideje alatt;
- az emberek viselkedésének megváltozása a járvány előrehaladtával;
- bejövő, kimenő és az országon áthaladó forgalom.
A lehetőségekre azonban jól rámutat a SEIR modell is, és a bizonytalanság mértékét is jól illusztrálja. Ami a járvány csúcsának konkrét idejét vagy a fertőzöttek számára vonatkozó jóslatokat illeti, bármelyik fenti modell téves lehet, de hozzátehetjük azt is, hogy a legtöbben ezt vagy ehhez nagyon hasonlót modelleket használnak a szakirodalomban.
Ahhoz, hogy csökkenteni tudjuk a járvány hatását, hogy a későbbiekben ne szoruljanak egy időben túl sokan kórházi ellátásra, a járvány teljes időtartama alatt arra kell törekednünk, hogy minél kevesebbet érintkezzünk másokkal, és betartsunk minden higiéniás szabályt, amire járvány esetén figyelni kell. Különösen fontos továbbá, hogy felhívjuk erre azok figyelmét, akik nem viselkednek felelősségteljesen, mert ők elsősorban nem magukat, hanem másokat, sőt közvetett módon tömegeket veszélyeztetnek. Fontos tudni, hogy az R0 egy átlagos érték: vannak, akik egyáltalán nem adják tovább a fertőzést, míg mások rengeteg embernek továbbadják. Utóbbiak viselkedésének megváltoztatásával lehetne jelentősen javítani az esélyeinken.
A szerző fizikus.
Kapcsolódó cikkek a Qubiten:
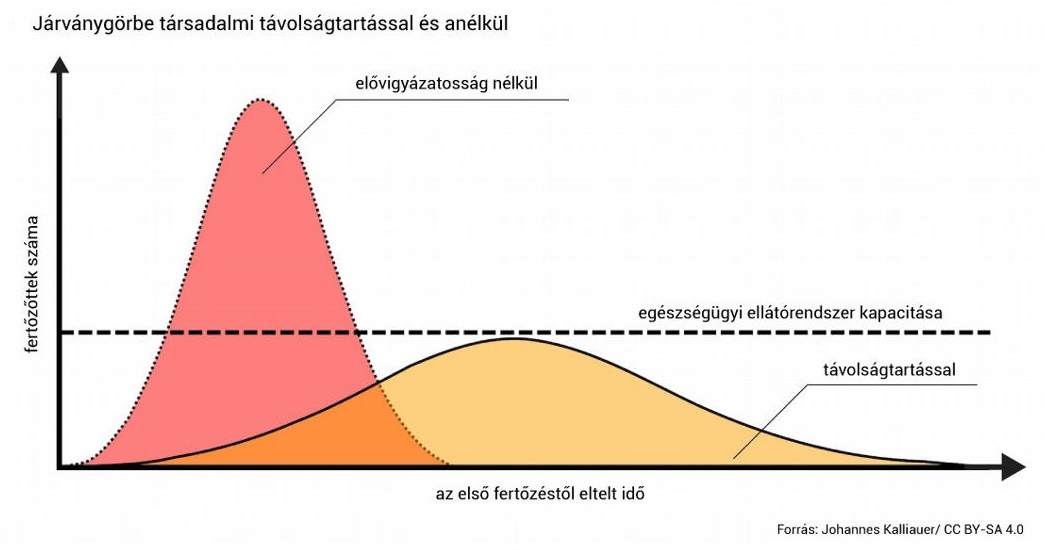
Mi az a hírhedt járványgörbe, és helyesen járunk-e el, ha megpróbáljuk kilapítani?
Joscha Bach, a mesterséges intelligenciával foglalkozó amerikai AI Foundation kutatója amellett érvel, hogy a görbe ellaposítása nem fog működni, és nem a görbét kell kilapítani, hanem a járványt kell megállítani. Igaza van, de ez nem változtat a jelenleg alkalmazandó intézkedéseken. Lássuk, miért!