Lehet-e minden koronavírus mellé fertőzésszámlálót állítani?

Rejtő Jenő halhatatlan regényhőse még magától értődő természetességgel szögezte le: nem lehet minden pofon mellé egy forgalmi rendőrt állítani. Ma már ez nem így van. Az utcák és közterek be vannak kamerázva, és ha valakit egy nem megfigyelt utcasarkon vernek pofon, az is tud utólag telefonjával fényképet készíteni a tettesről. Elvileg tehát a pofonok megszámlálhatóak: a testi kapcsolat során „A” adja, „B” meg kapja a pofont. Ha „A” notórius verekedő, akkor egy este során akár több más emberbe is beleköthet, többeket is felpofozhat. Ha feltételezzük, hogy a megpofozott emberek egy része a dühtől vezérelve legalább egy másik embert, vagy esetleg többet is felpofoz, akkor járványszerűen fog terjedni a pofozkodás. A lényeg az, hogy az összes elcsattant pofon elvileg megszámlálható, csak sokat kell hozzá fényképezni.
R0 és R bizonytalanságai
Amikor a koronavírus-járványt modellező, értelmező és magyarázó tudós kollégák a COVID-19 betegséget terjesztő vírus fertőző képességét tárgyalják, akkor implicit módon valami hasonló szituációt feltételeznek: van egy fertőzött személy, aki megfertőz egy vagy több másik személyt. Így gondolja ezt az utca embere is. A kapcsolatot két mutató hivatott kifejezni: az R0 (basic reproduction rate), ami azt mutatja, hogy a járvány kezdetén, mindenfajta előzetes immunitás és korlátozás hiányában, 1 megfertőzött ember átlagosan hány másik embert fertőz meg (és ezzel lehetőséget ad a vírus „tömegének” szaporodására), valamint az R (effective reproduction rate), amely egy olyan érték, amely a járvány idején, egy tetszőleges későbbi, már befejeződött időpontban mutatja meg ugyanezt. Tehát azt, hogy egy fertőzött ember (az alatt az idő alatt, amíg fertőzőképes) átlagosan hány másik embert fertőz meg az adott populációban. A gyakorlatban populáción a járványügyi döntéseket hozó szakemberek mindig egy adott ország teljes népességét értik, jól lehet – elvileg – mindenki tudja, hogy ez az R érték egy adott időpontban országon belül is erősen különbözik (városokban magasabb, mint vidéken). A sikeres járványügyi stratégia logikája szerint minden R-en múlik: ha R>1, akkor nagy a baj, mert a fertőzések száma exponenciálisan nő, ha R-et sikerül 1 alá szorítani, akkor a járvány előbb-utóbb „magától” lecseng.
Természetesen a modellezők és a járvány lényegét csak felületesen ismerő szakemberek is tisztában vannak azzal, hogy a vírussal fertőzött emberek száma közvetlenül nem mérhető a szükséges pontossággal. De azt állítják, hogy modellszámítással, mérhető kiinduló adatokból (pl. megbetegedések, kórházba kerülés, felgyógyulás, COVID-halálozás) R nagysága minden időpontra visszamenőlegesen megbecsülhető, és ennek alapján a paraméterek feltételezett jövőbeni változásait számszerűsítve R előre is jelezhető. Ez sajnos nem igaz. Már a járvány kezdetén világossá vált, hogy a nyilvántartott fertőzöttek száma szoros korrelációban áll az elvégzett tesztek számával. Ha az egészségügyi rendszer képes a korábbinál többet tesztelni, akkor újabb és újabb fertőzötteket lehet „felfedezni”. Ez ceteris paribus magasabb R értéket fog eredményezni. De a változásnak nem az az oka, hogy több a fertőzés, hogy 1 fertőzött több másik embert fertőz meg, hanem az, hogy több mérés (tesztelés) történt. A pofozkodós példa ebből a szempontból is megvilágító erővel bír. Minél több az utcai kamera, annál több pofont fognak megszámolni a rend őrei.
Ez a cikk két, egymással összefüggő állítást próbál megfogalmazni:
A „minden az R-en múlik” állítás valójában tautológia. Ehhez nincs szükség sem mérésre, sem modellezésre. A pofonok hasonlatával élve, csak annyit mond, ha a megpofozott emberek átlagosan több mint 1 embert pofoznak meg, akkor a pofozkodási járvány megállíthatatlan.
Miután a vírusok mellé nem lehet fertőzés-számláló epidemiológust állítani, semelyik időpillanatban nem lehet meghatározni a fertőzések (flow) és/vagy a megfertőzött emberek (stock) számát. Ez nem mérési vagy becslési probléma – a vírus és az általa okozott betegség sajátosságaiból következik. Más járványos betegségek (pl. pestis, lepra) esetében a fertőzésnek egyértelmű, jól látható és maradandó tünetei vannak, ezért a fertőzöttek száma (mind stock, mind flow dimenzióban) tetszőleges pontossággal megállapítható – még tesztelésre, sőt hőmérőzésre sincs szükség. (Miután a betegség teszteléséről és a tesztek megbízhatóságáról sok információ került napvilágra az elmúlt napokban, az ezzel kapcsolatos nehézségekre itt és most nem kell kitérnünk.)
A SARS-CoV-2 vírus sajátosságairól, terjedéséről egyre többet tudunk, de még mindig keveset. Azt azonban biztonsággal állíthatjuk, hogy a fertőzési folyamat nem hasonlítható a pofozkodáshoz. Miért nem? Először is azért, mert a fertőzés többféle módon is terjed, és nincs biztos ismeretünk arról, hogy ezek külön-külön mennyire gyakoriak. Nézzük csak a két legfontosabbnak gondolt útvonalat.
Amikor „A*” fertőzött személytől köhögéssel, tüsszentéssel, beszéd közben vagy a levegő kilégzésével indulnak el vírusok milliárdjai (!) a külső környezet irányába, akkor az éppen ott tartózkodó, „B” nem-fertőzött személy egy bizonyos, előre nem ismert valószínűséggel fog megfertőződni. Az is lehetséges, hogy „A*” nemcsak „B”-t, hanem „C”-t is megfertőzi, és az is, hogy „A*” csak B-t fertőzi meg, és „B*” adja tovább a fertőzést „C”-nek, rövidebb vagy hosszabb idő múlva. Az időtényező fontos. A megfertőzött „B*” személy eleinte fertőz, aztán amikor már tünetei vannak, akkor esetleg már karanténba kerül.
Még bonyolultabb az eset, ha „A*” fertőzött személy tárgyak érintése során hagyja hátra maga mögött a fertőző vírusok kritikus tömegét (pl. ajtókilincsen, korláton, cipőjével az utcán). Ebben az esetben ugyanis „D”, „E”, „F” stb. nem-fertőzött emberek megfertőződése időben is elválik a fertőzést okozó vírusok kiszabadulásától.
A második esetben, ha a fertőzés tárgyi közvetítés útján történik, akkor az utólagos „contact tracing” teljességgel lehetetlen, mert a vírus csak korlátozott ideig marad fertőzőképes a tárgyak felületén, vagyis a fertőzés bekövetkezte után nem marad nyoma. Ezt az utóbbi tényt érdemes ahhoz a 2006-os esethez hasonlítani, amikor az orosz titkosszolgálat radioaktív polóniummal ölte meg Alekszandr Litvinyenko egykori KGB-ügynököt Londonban. A példa azért jó, mert a polónium nagyon kis adagban is halálos méreg – olyan kis adagban is, ami szabad szemmel egyáltalán nem látható (ahogyan a vírus sem). A merénylet után a három héttel később (!) végzett nyomkövetés azért lehetett mégis sikeres, mert a polónium izotópjainak felezési ideje években mérhető – és nem órákban, miként a koronavírus esetében. Sugárzásmérővel ki is lehetett deríteni, hogy az orosz ügynökök utcáról utcára merre jártak, és merre járt a megfertőzött áldozat, miután megkapta a halálos fertőzést. A vírus esetében a kontakt-visszakövetés szinte lehetetlen, hacsak nem zárt közösségekről van szó.
Márpedig az elmúlt hetek során megtapasztaltuk, hogy a koronavírus fertőzések legfontosabb gócpontjai Európa-szerte éppen a speciális adottságokkal rendelkező, zárt intézmények: az idősek otthonai és a COVID- betegeket fogadó kórházak. Logikusnak tűnik azt feltételezni, hogy az idősek otthonában, ahol definíció szerint idős, krónikus betegségekkel küzdő, legyengült immunrendszerű emberek élnek, sokkal kisebb mennyiségű vírus is képes sok embert megfertőzni, mint bárhol másutt. Ezért egy ilyen környezetben megjelenő „A*” fertőzött egymaga is képes nagyon sok embert megfertőzni. Nem azért, mert ő éppen szuper-terjesztő, hanem az adott környezet sajátosságai miatt.
Valami hasonló folyamat kell, hogy végbe menjen a már megfertőzött betegeket gyógyító kórházakban is, ahol vélhetően ugyancsak magas a víruskoncentráció (a nagyon alacsony felezési idő ellenére is!), de az ott dolgozó emberek nagyon hosszú időt töltenek el, vagyis összességében több vírussal találkoznak. Itt sem lehet utólag megszámolni a fertőzési alkalmakat, merthogy a kórházban definíció szerint sok hasonló módon megfertőzött ember tartózkodik egyszerre. Nincs értelme azt kutatni, hogy a nagybeteg Jancsi bácsi vagy Mari néni külön-külön hány egészségügyi dolgozót fertőzött meg, és annak sem, hogy a kezelt betegek számát függvényszerű kapcsolatba hozzuk a kórházban megfertőződött dolgozók számával. Például ha 30 beteg 1 hét alatt 3 egészségügyi dolgozót betegített meg, akkor 60 beteg 6 kórházi dolgozót fog megfertőzni. Ez gyakorlati és nem matematikai kérdés. Eléggé nyilvánvalóan tűnik, hogy az ilyen fertőzések száma leginkább attól függ, hogy mennyi és milyen minőségű védőfelszerelés áll rendelkezésre az adott kórházban. Ma már tudjuk, sokkal jobb lett volna a járvány kezdetétől mindenütt ezen veszélyközpontok védelmére koncentrálni.
A matematikai és/vagy gondolkodási modellek többsége az R0 értéket nagyobbrészt afféle biológiai állandónak tekinti – hasonlóan ahhoz, ahogyan a szülészek az ikerszülések valószínűségéről beszélnek (kb. 1,6%). A becslés során ugyanis két vírusspecifikus tényezőt és „csak” egy társadalmi tényezőt vesznek figyelembe.
A vírus fertőzőképességét (ha „A*”10 emberrel találkozik, akkor hány embert fertőz meg);
Átlagosan mennyi ideig marad „A*”, „B*” stb. fertőzőképes;
Egy időintervallum alatt „A*”, „B*” stb. hány másik emberrel találkozik.
A mostani számítások egyik kiindulópontja Kucharski et al. 2020. január 28-án megjelent online publikációja, amely szerint R0 értéke Wuhanban a járvány kitörésekor 3,0-ra volt becsülhető – az 1,5 – 4,5 konfidencia-intervallumon belül. Az Epidemic Calculator programhoz megadott irodalomjegyzék még 9 további hasonló, kínai adatokra alapozott forrást jelöl meg. Ezek többsége ugyancsak 3 körüli R0 értéket ad meg, de van egy hivatkozott tanulmány, amely a teljes kínai minta alapján 6,5-es értéket valószínűsít a hozzá tartozó 5,7-7,2 konfidencia-intervallumon belül. Akármi is volt a kínai Wuhanban a járvány tényleges reprodukciós rátája a különféle korlátozások (intervenciók) előtt, hihetőek azok a számítások is, amelyek Kínán belül 3 és 6 közötti R0-értékeket becsültek. Merthogy eléggé nyilvánvaló, hogy a földrajzi, gazdasági és társadalmi feltételek Kínán belül is igen eltérőek, és még inkább torz a kiinduló becslésünk, ha azt feltételezzük, hogy New Yorkban vagy Budapesten is ugyanolyan sebességgel terjed a járvány, ha nem csinálunk semmi korlátozást. Egyébként az elmúlt hetek éppen ezt a feltételezést igazolták: amikor még sem New Yorkban, sem Budapesten nem érvényesültek a korlátozások (kb. március 15. előtt), akkor már drámaian különbözött a járvány lefolyása a két városban. Olyannyira, hogy Oroszi Beatrix, az Innovációs és Technológiai Minisztérium járványügyi szakértője egy minapi előadásban úgy fogalmazott, hogy a magyar populációt tekintve még ma is csupán endémiáról (szűk területeken előforduló megbetegedésekről) beszélhetünk és nem pandémiáról.
Könnyű belátni, hogy a tényleges R0 értékeket visszamenőlegesen sem lehet majd megállapítani. Más modellezők ezért úgy gondolják, hogy az előrejelzések szempontjából az R0 érték valójában érdektelen. A modelleket úgy érdemes kalibrálni, hogy időben a járvány kiinduló pontjának a 100. vagy 1000. halálesetet tekintjük, amikortól kezdve már bizonyosan érvényesülnek a járványkorlátozó intézkedések. Nem ismerem az efféle modelleket részleteiben, de azt gyanítom, hogy előrejelzésként egészen másféle eredményt lehet kapni akkor, ha a modellt a 100. halálesettől vagy az 1000. halálesettől számítva építjük fel.
Összefoglalóan tehát azt mondhatjuk, hogy valójában sem az R0, sem az R nem tekinthető biológiai állandónak, számszerű értékeiket a vírus jelenlegi természete, a társadalmi háló(k) szerkezete, valamint a járvány miatt elrendelt korlátozások milyensége együttesen határozza meg. Jelenlegi, korlátozott ismereteink birtokában ezért nem lehet megbízhatóan előre jelezni a járvány terjedését – sem az Egyesült Államokban, sem Magyarországon, sem Svédországban.
Mi több, van még egy talán a fentieknél is fontosabb problémája a járvány előrejelzésének. A vírus mutálódhat. Számos vírus esetében – ideértve az influenzavírusokat és egyes koronavírusokat is – a tapasztalat is ezt igazolja. A térbeli tovább terjedéssel változhat a vírus fertőzőképessége, a betegséggel járó tünetek súlyossága és az elhalálozás valószínűsége. Érzésem szerint alapjában csak ez fogja meghatározni a világjárvány további alakulását. A viszonylag biztosnak mondható halálozási adatok mintha azt mutatnák, hogy Nyugat-Európában is és Amerikában is „szelídül” a vírus (ami persze nem zárja ki, hogy később durvulni fog). Bízzunk a szelídülésben! Egy jó vakcina, egy nagy valószínűséggel biztos gyógyulást kiváltó gyógyszer már csak hab lenne a tortán.
Megváltozik-e a világ a járvány miatt?
Alapjában véve filozófiai és politikai választás kérdése, hogy a közel 8 milliárd fős emberiség öt kontinensen átnyúló társadalmi hálóit az új típusú koronavírus megjelenése miatt megváltoztathatónak és megváltoztatandónak gondoljuk-e. Az alacsony átfertőzödöttségi szint miatt világméretekben (és Magyarországon is) az a helyzet, hogy az ember-ember közötti érintkezések 90-95 százaléka nem érinti érdemben a járvány terjedési sebességét. De ahogyan nő a fertőzöttek száma, nő a fertőzés lehetőséget jelentő találkozások száma is. Az egyének közötti fizikai távolságtartás (szerencsétlen angol megnevezéssel: social distancing) feltételezhetően csak ideiglenesen változtat a társadalmi kapcsolatok szerkezetén, de kétségtelenül csökkenti a vírusok „tömegét” – annyiszorosan, amennyivel csökken a fertőzés esélye az új, átmeneti viselkedési normák terjedésével. Számszerűen: ha harmadára csökken a fertőzés esélye egy találkozáskor (mert gyakran mosunk kezet, 2 méteres távolságot tartunk, kesztyűt hordunk stb.), akkor 3-szor annyi találkozás kell ugyanannyi fertőzéshez, mint alapesetben. A regionális korlátozás (országok, városok határainak lezárása) a nagy populációt felszabdalja részekre, a közöttük lévő kapcsolatokat töredékre csökkentve, ami a vírus terjedést szintén lassítja.
Fülig Jimmy pofonhasonlata mindenesetre segít a lehetőségek végiggondolásában. Ha rábeszéljük az embereket, hogy 1 hónapra, 6 hónapra vagy egy éven át senki ne akarja továbbadni a pofont, akkor egy időre a járvány lecseng. De ha ez a határidő lejár, és az emberek ismét visszatérnek a „normális” viselkedéshez, akkor a pofozkodási járvány kezdődik elölről, és a járványóra újraindul.
A szerző (egészségügyi közgazdász, az MTA doktora) köszönettel tartozik Telcs András matematikusnak, egyetemi tanárnak értékes tanácsaiért. A cikkben leírtakért természetesen csak a szerző tartozik felelősséggel. A koronavírus- járvány eddigi hazai tapasztalatairól a szerzőnek három cikke jelent meg az Élet és Irodalom hasábjain itt, itt és itt.
Kapcsolódó cikkek a Qubiten:
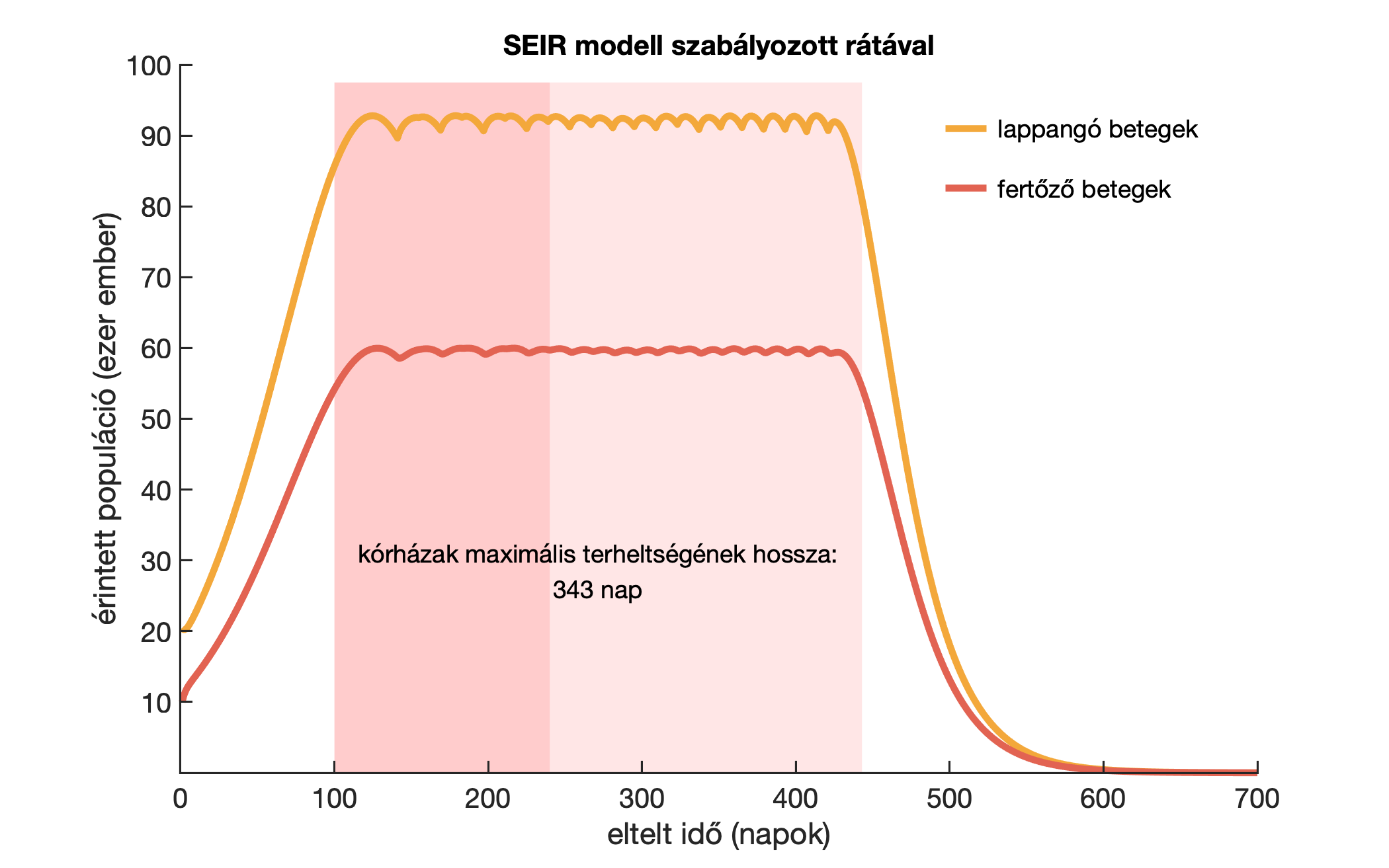
Hogyan alakíthatjuk aktívan a járványgörbét, és miért elengedhetetlen ehhez a tesztelés?
A vírustesztekből származó mérési eredmények rendkívül fontosak a kutatóknak a helyes modellezéshez: általuk lehet meghatározni a megfelelő intézkedések mértékét és időzítését, ami jelentősen képes befolyásolni a járvány terjedését.
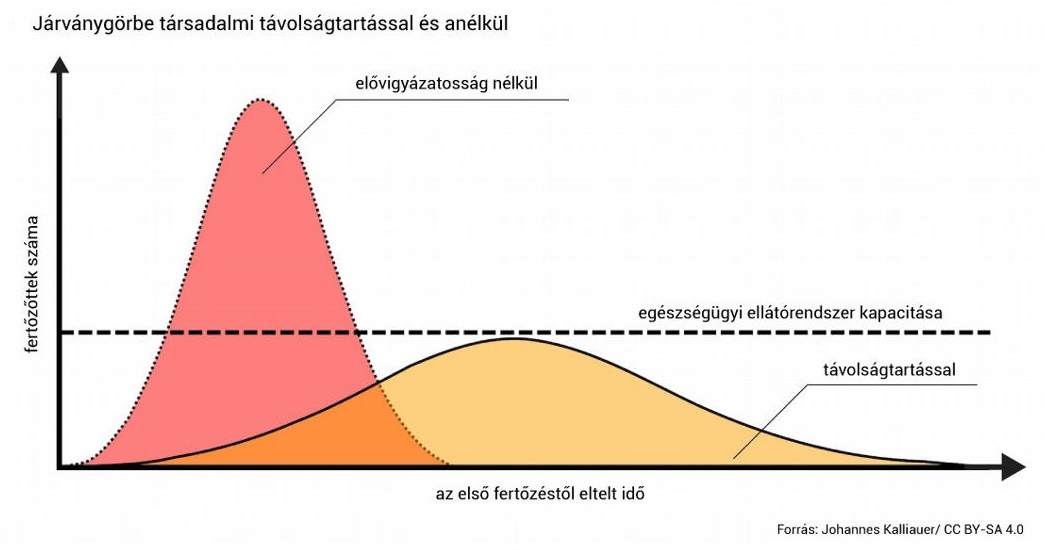
Mi az a hírhedt járványgörbe, és helyesen járunk-e el, ha megpróbáljuk kilapítani?
Joscha Bach, a mesterséges intelligenciával foglalkozó amerikai AI Foundation kutatója amellett érvel, hogy a görbe ellaposítása nem fog működni, és nem a görbét kell kilapítani, hanem a járványt kell megállítani. Igaza van, de ez nem változtat a jelenleg alkalmazandó intézkedéseken. Lássuk, miért!
A járványdinamika segít abban, hogy megértsük, miről szólnak a mostani intézkedések
Minél kisebb az egyszerre jelentkező esetszám, annál kevésbé van leterhelve az egészségügy. A jelenlegi intézkedések ezt az időbeli elhúzást kívánják elérni, amivel a járvány időtartamát kitolják ugyan, de az egészségügy leterheltségét csökkentik.
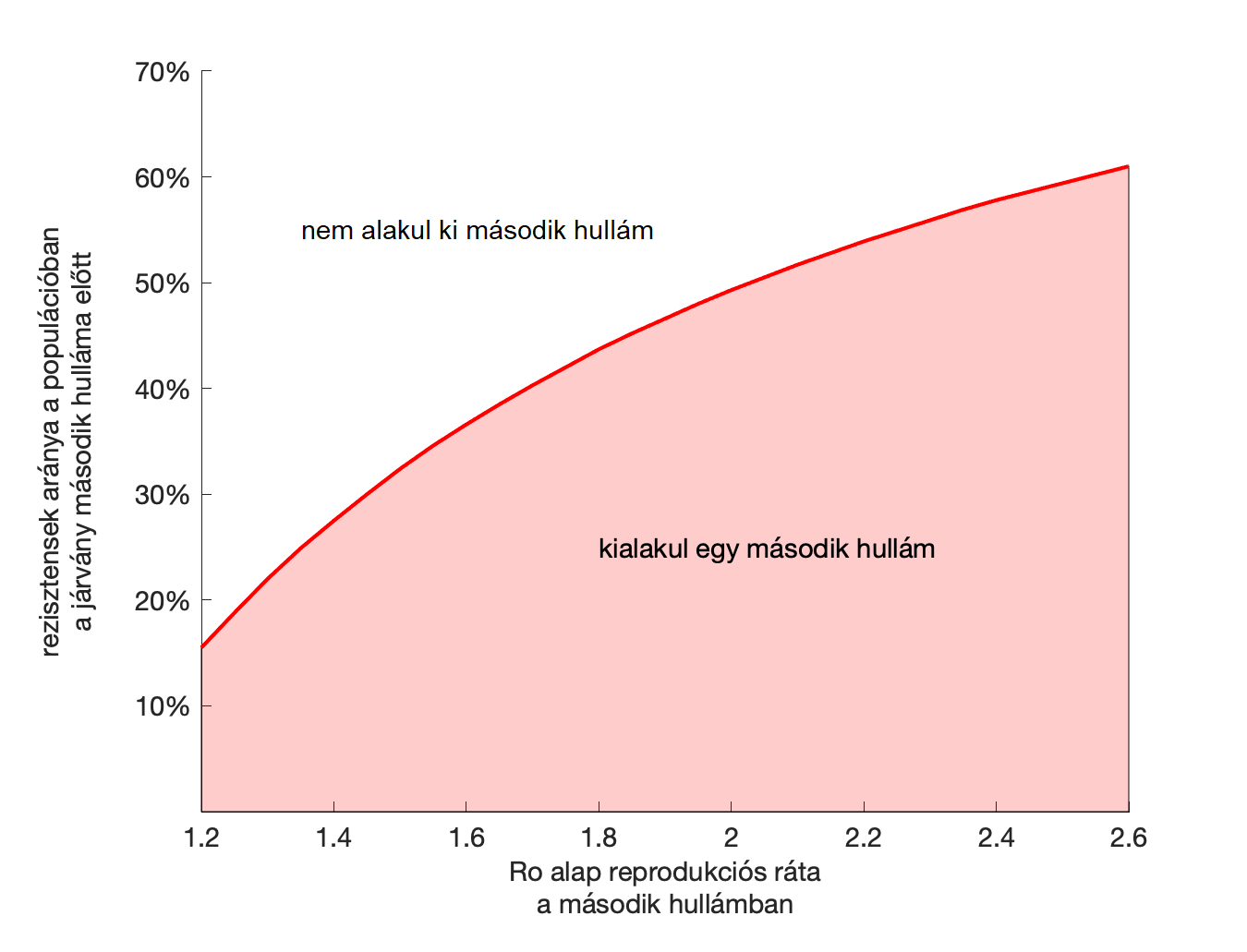
Meddig bénítja meg a világot a járvány, és lesz-e Magyarországon is második hullám?
Hogy nem túl rózsásak a kilátásaink a koronavírus elleni küzdelemben, az nem kifejezés: ha nem sikerül kifejleszteni a vakcinát a SARS-CoV-2 ellen, és a nyájimmunitás sem alakul ki, még sokáig velünk élő járványügyi intézkedésekkel kell számolnunk a hétköznapjainkban.