Hogyan alakíthatjuk aktívan a járványgörbét, és miért elengedhetetlen ehhez a tesztelés?

Járványdinamikai cikksorozatom előző részében arra hívtam fel a figyelmet, hogy abban az esetben, ha netalán nem tudnának időben vakcinát fejleszteni a kutatók, akkor a járvány második hullámára is számíthatunk, ha nem fertőződik át eléggé a lakosság. Ennek feltételeit vizsgáltam a SEIR járványdinamikai modell segítségével, és kiderült: abban az esetben, ha a járványgörbét annyira ellaposítjuk, hogy ne terhelje túl az egészségügyet, nem fog kialakulni a nyájimmunitás, ami megvédheti a társadalmat egy második hullámtól és a hosszan tartó járványügyi intézkedésektől. A differencia meglehetősen nagy volt, mert a modellszámítások szerint ha a magyar egészségügy teljesítőképességének korlátain belül maradunk, a lakosságnak csak nagyjából a harmada fertőződik át a járvány első hullámával, miközben kétharmad átfertőződésére lenne szükség ahhoz, hogy kialakuljon a nyájimmunitás.
Egy nappal később jelent meg egy másik cikk, amiben a világ vezető epidemológusait idézték, akik pontosan ugyanerre a problémára hívták fel a figyelmet. Eszerint a járványgörbe ellaposítása az egészségügyi krízis elkerülése végett szükséges, ugyanakkor azzal jár, hogy később a járvány még több hullámban végigsöpörhet a világon. Természetesen mindenki reménykedik abban, hogy időben sikerül kifejleszteni egy vakcinát – egy hatékonynak tűnő jelöltet már egereken teszteltek –, de a sikert nem vehetjük biztosra; ugyanakkor már most kellene rendelkeznünk egy hosszú távú stratégiával az egészségügyi és gazdasági katasztrófák elkerülése végett.
A Harvard fent említett epidemológusai köztes megoldást javasolnak, és hasonló felvetéssel álltak elő izraeli kutatók is: nevezetesen azzal, hogy időszakosan, akár heti rendszerességgel kontrolláltan lazítva majd szigorítva az intézkedéseken tartsuk a járványgörbét mesterségesen az egészségügyi rendszer teljesítőképessége határának közelében, és ezt hosszú távon tartsuk fenn minél több teszteléssel és kontaktkutatással kiegészítve, nehogy az egész tervet bedöntse egy váratlanul kialakuló megfékezhetetlen gócpont. Magyarán ne engedjük, hogy a járvány gyorsan és intenzíven terjedjen, mert az katasztrofális mértékben megterhelné az egészségügyet, de ne is egyetlen hosszan tartó drasztikus intézkedéssel kezeljük a problémát, mert azzal a tetőzéskori terhelést le tudjuk csökkenteni ugyan, ezzel együtt viszont az egész járványgörbe annyira lecsökken, hogy a járvány végére nem fertőződünk át eléggé a nyájimmunitáshoz, ráadásul az ehhez szükséges hosszan tartó korlátozások a gazdaságot is megbénítják.
Szemléletesen arról van szó, hogy amennyiben a fertőzés reprodukciós rátáját hosszabb időtávon fixnek vesszük, ahogy mi is tettük korábbi szimulációinkban, akkor a járványgörbe (piros vonal) mindenképpen hupli alakú, és szigorú intézkedésekkel csak a hupli magasságát tudjuk csökkenteni, de az alakját nem tudjuk befolyásolni. A maximum csökkentése ráadásul ki is szélesíti a görbét, elhúzza a járványt, és még az átfertőződés mértéke is csökken.

Ha azonban mesterségesen, aktívan kontrollálni tudjuk a rátát, a járványgörbe alakját talán jobban is tudjuk alakítani, és elérhetjük, hogy egy csúcsos hupli helyett hosszan és laposan tetőzzön. Ezt az aktív kontrollt természetesen csak modellezéssel lehet megoldani, mert előre kell tudnunk jósolni, hiszen amit ma teszünk intézkedésekkel való beavatkozással, annak hatása később érvényesül a járványgörbén. A modellek használatához, azonban a modellek paramétereinek helyes beállítására is szükség van, amihez megfelelő mérési adatok kellenek. Ezért is lennének nagyon fontosak a tesztek, mégpedig a szisztematikus véletlen tesztelések, amit több országban már elkezdtek, azonban ezt helyi szinten is meg kell tennünk ahhoz, hogy releváns adatokat nyerjünk, mert minden országban mások a helyi körülmények.
Müller Cecília országos tisztifőorvos egy hete azt mondta, hogy a tesztelés információt nyújt ugyan, de a járvány terjedésében nem játszik fontos szerepet és az elvégzése csupán orvosszakmai kérdés. A fentiek fényében láthatjuk, hogy ahhoz, hogy a járványt szabályozni tudjuk a teszteléssel szerzett információk nagyon fontosak, és ilyen közvetett módon mégis szerepet játszhatnának a járvány terjedésében. Ezen kívül az intenzív tesztelés és kontaktkutatás a járvány legelején ugyancsak jelentősen befolyásolhatta volna a terjedést, és ha kezdetektől fogva nagyon szigorú kéthetes karantént rendeltek volna el a beutazóknak, ahogy például Tajvan vagy Nauru teszi és tette, akkor a járvány akár teljesen elfojtható lett volna, de erről már nyilván lekéstünk az összes európai országgal együtt.
Másrészt az alapos tesztek nagyon fontosak olyan gócpontok kialakulásának megelőzéséhez vagy kezeléséhez, mint például az idősotthonok, a kórházak vagy a börtönök. Ez szinte elengedhetetlen a katasztrófák elkerülése érdekében. És a tesztelés nagyon fontos lenne ahhoz is, hogy visszamehessenek dolgozni azok, akik már átestek a betegségen, hiszen az ő számuk heteken belül elérheti a több tízezres nagyságrendet.
A pontos modellek használatához tehát – amik támogatni tudnák a megfelelő intézkedések meghozatalát és időzítését – a kutatók számára szükség lenne mérési adatokra. Tegyük fel azonban most egy pillanatra, hogy megvannak ezek az adatok, és a modellekkel pontosan előre tudjuk jósolni a járvány alakulását, és a paraméterekkel is tetszőlegesen játszhatunk.
Ahogy az előző cikkben, tegyük fel, hogy az egészségügyi rendszer egyszerre 60 000 fertőzöttet bír el, ennek 5 százaléka ugyanis intenzív ellátásra és lélegeztetőgépre szorul. Tegyük fel, hogy a korlátozásokat kéthetenként változtatva, szükség szerint szigorítva vagy enyhítve, képesek vagyunk elérni azt, hogy soha ne menjen a határérték fölé a betegek száma. Ehhez tehát mindig előre kell kalkulálnunk, és amennyiben az aktuális korlátozásokkal számolt jóslatunk túllépné a megengedett határértéket, akkor megfelelő mértékben szigorítani kell az intézkedéseken, ha viszont nem lépi túl, akkor a számítások szerinti mértékben lehet lazítani. Ha ezt jól csináljuk, akkor elérhető, amit az amerikai szakértők is felvetettek, lásd az alábbi ábrán.
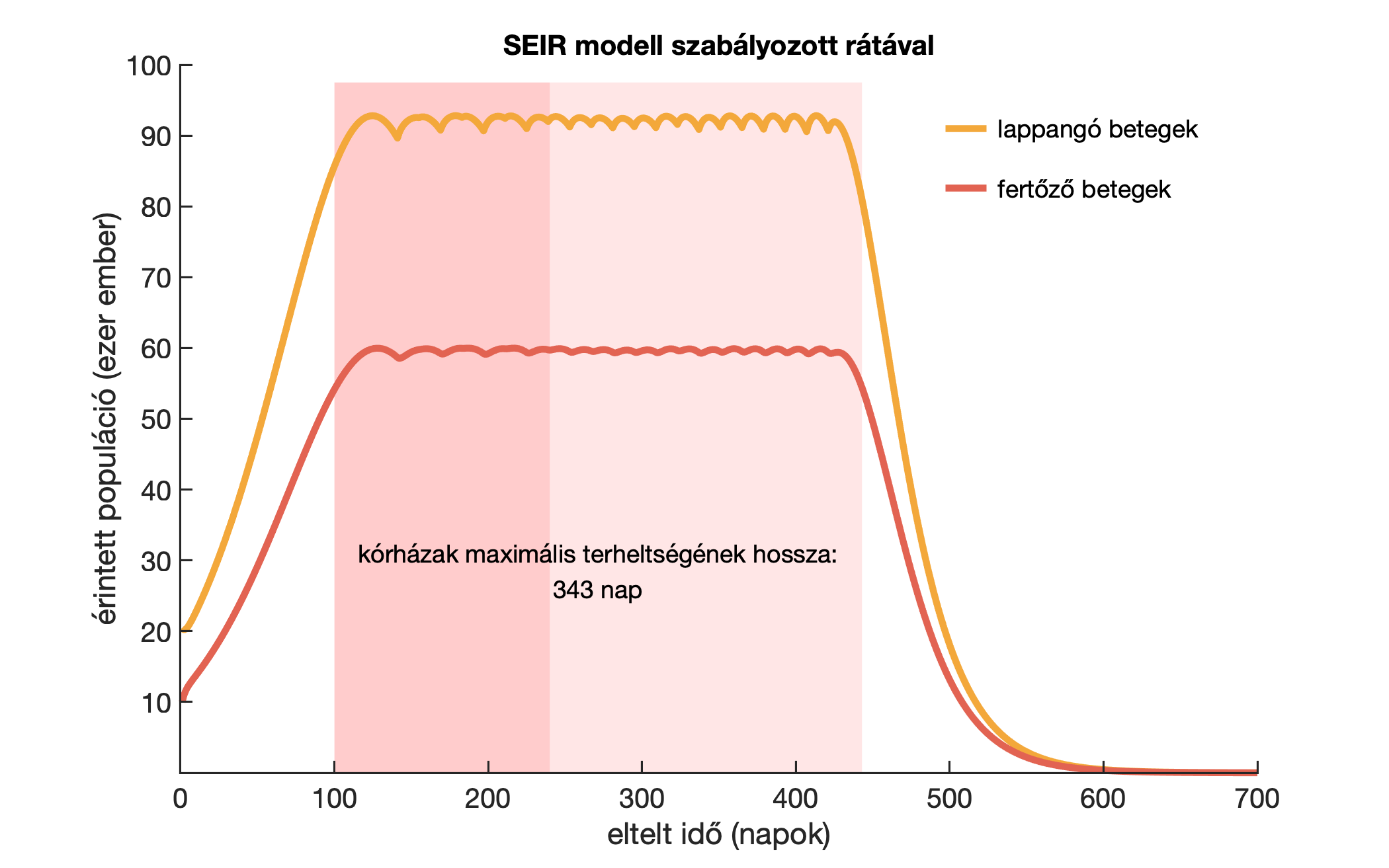
Az ábrán azt láthatjuk, hogy ilyen módon valóban elérhető egy hosszan és laposan tetőző járványgörbe. A tetején látható pici fluktuációk a kéthetes szabályozás hatásai. A szimuláció szerint a kórházak maximális terheltsége majdnem egy évig fennál (343 nap) és a tetőzés elejétől számítva 125 napig (sötétebben satírozott tartomány) fenn kell tartani elég szigorú járványügyi korlátozásokat (1,5 alatti reprodukciós rátát). 17-18 hét után azonban már viszonylag nagy ütemben lazíthatók a korlátozások. Ami az ábrán nem szerepel még, hogy egy ilyen forgatókönyv szerint a járvány végére a populáció majdnem 80 százaléka átfertőződne, ami már bőven elég a nyájimmunitáshoz, tehát nem alakulna ki második hullám – legalábbis addig nem, amíg tart az immunitás.
Valamit valamiért
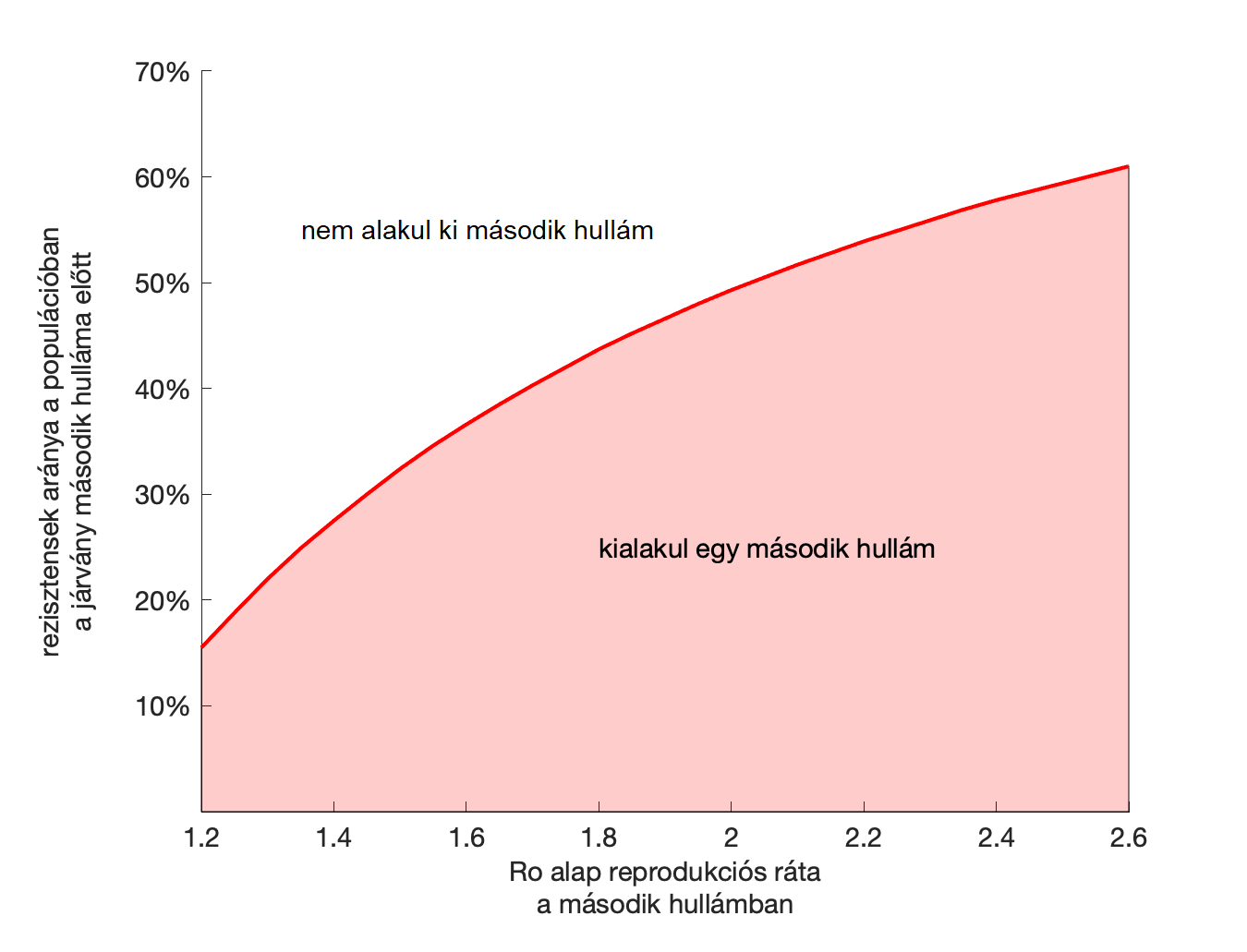
Előző cikkünk végén láttuk, hogy a nyájimmunitás kialakulásához már 60 százalékos átfertőződöttség is elegendő, tehát van még mozgástér, és ha nagyobb ingadozásokat is megengedünk, illetve nem ragaszkodunk a konstans egészségügyi terheléshez, akkor ennek az elképzelésnek különféle variációi még működőképesek lehetnek. Azonban nyilván itt is igaz, hogy valamit valamiért: ha a szigorításokat hosszabb időszakokra enyhíteni szeretnénk, akkor a járvány jobban elhúzódik.
Meg kell jegyeznünk, hogy a fenti szimulációban természetesen vannak még bizonytalanságok. Korábban azt mondtuk, hogy a járvány lefutása leginkább az R0 reprodukciós rátától függ, de mivel itt most éppen ezt szabályozzunk, ezért a többi paraméter válik fontossá, amit korábban fixen tartottunk. Ezek pedig a lappangó fázisban átlagosan eltöltött TE idő és a fertőző fázisban átlagosan eltöltött TI idő. Fontos, hogy itt mindkét értéket a modell szempontjából kell tekintenünk, tehát nem klinikai értelemben kell értelmezni őket, hanem azt kell megvizsgálnunk, hogy a betegség effektíve mettől meddig fertőz átlagosan. Ez a lappangási időt nem annyira érinti, mert a lappangókról nem tudjuk, hogy lappangók, de a felismert, tünettel rendelkező fertőzöttek már tudják magukról, hogy fertőznek, és ezért is, meg kényszerűségből is kevésbé fertőznek: jó esetben karanténban vagy ágyban fekszenek. A lényeg, hogy ezeknek az időtartamoknak is hatalmas a variabilitása emberről emberre, és itt a modell csak átlagos értékeket vesz figyelembe.
Hozzá kell tennünk, hogy bár a fenti járványgörbe platójának hossza a fertőzöttek jelenlegi számától és a jelenlegi rátától épp nem függ érzékenyen az aktív kontroll miatt, a tesztek mégis fontosak. Egyrészt azért, mert a modelleket az általuk szolgáltatott adatokra illesztve lehet a fenti TE és leginkább TI paramétereket megbecsülni, másrészt azért, mert a járvány felfutásának elején nagyon érzékeny a dolog, ezért a mérési adatok segítségével lehet felmérni a valós állapotot és azt, hogy pontosan mikor érdemes intézkedéseket hozni.
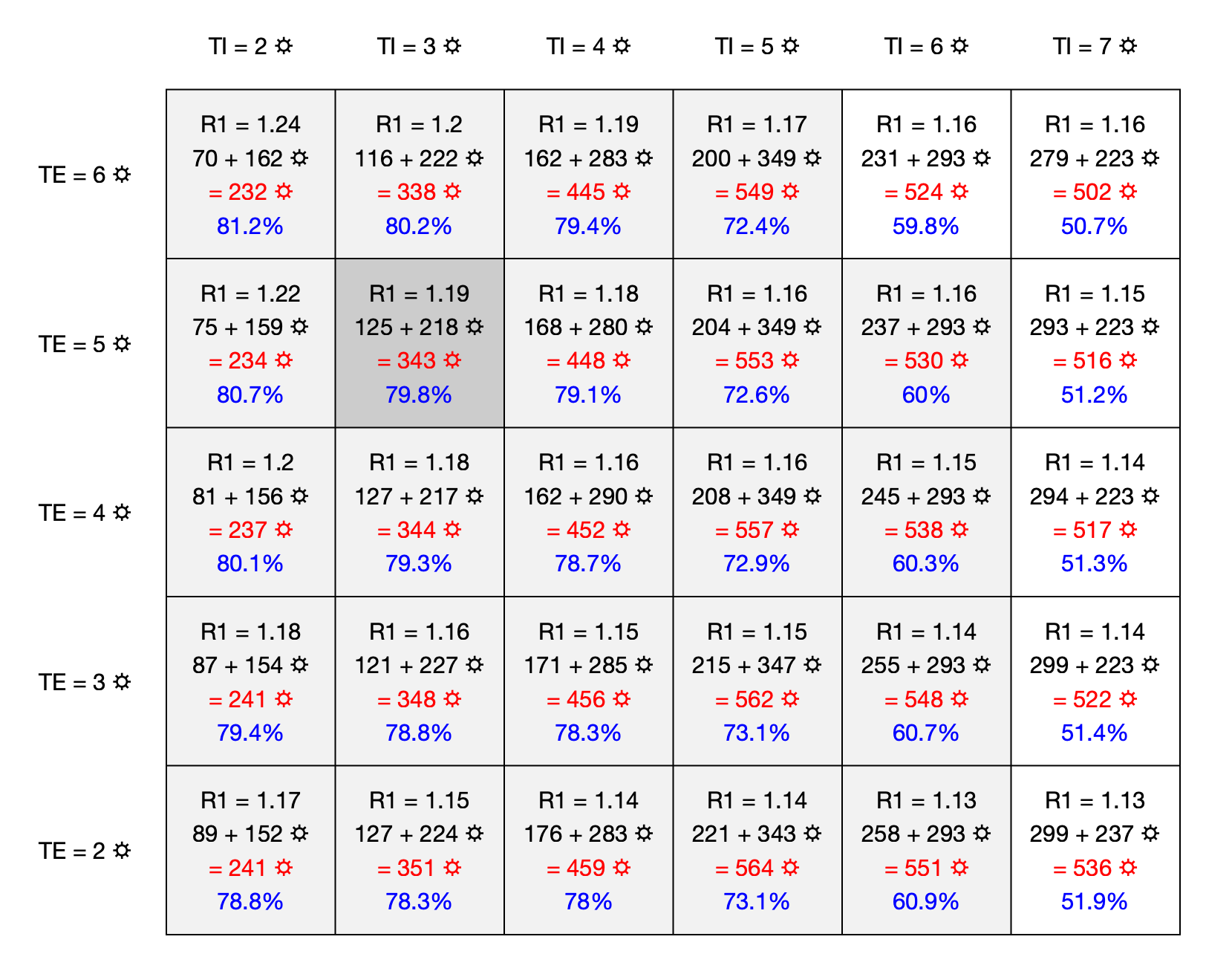
Korábbi cikkünkben szegedi kutatók cikkére hivatkozva TE = 5,1 nap (korábban 1/σ), és TI = 3,3 nap (korábban 1/𝛾) értékeket használtuk, de ha netán ezekre időközben – vagy Magyarországra vonatkoztatva – jobb becslés adódik, akkor evégett most táblázatos formában közöljük, hogy milyen eredményeket ad különböző TE és TI paraméterkombinációkra a fentiekben ismertetett aktívan kontrollált SEIR modell.
A táblázatban rendre az alábbi értékeket olvashatjuk ki a cellákból: a kórházi terhelés kezdetére elérendő legszigorúbb reprodukciós ráta (R1), ami később már csak enyhül. Alatta a kórházi terhelés napjainak száma pirossal, amit két részre bontottunk: az első rész annak az időtartamnak a hossza, amíg a szigorúbb 1,5 alatti rátáknak kell érvényesülniük (a kórházi leterhelés elejétől számítva). Legalul a kék százalék pedig a lakosság átfertőződési aránya a járvány végére. Sötétszürkével jelöltük azt a cellát (illetve paraméterkombinációt), amire a fent közölt járványgörbe vonatkozott. Halványabb szürkével láthatók azok a paraméterkombinációk, ahol az átfertőződés még megfelelő mértékű lenne ahhoz, hogy a járványnak ne alakuljon ki második hulláma. Mindez természetesen arra vonatkozik, ha nem válik közben tömegesen elérhetővé vakcina.
A cikk végén még egy lehetőséget és szimulációt szeretnék bemutatni. A fenti forgatókönyv lényege az volt, hogy a rátát aktívan szabályoztuk, de ennek az az ára, hogy előre kell tudni jósolni. Természetesen a ráta a valóságban is változhat, például azért, mert minél több a fertőzött, minél több halálhírt hallunk, átlagosan annál elővigyázatosabbak leszünk. Persze abban a nem kívánt esetben, ha az egészségügyi rendszer közben összeomlik, vagy nincs elegendő védőfelszerelés, akkor ez megváltozhat, de tegyük fel, hogy minél több a fertőzött, annál jobban csökken a szociális interakciók száma személyes elővigyázatosságból. Vajon nem képes arra ez az önszabályozó folyamat, ami egy folytonosan változó reprodukciós rátát eredményez, hogy elérje ugyanazt a hatást, mint az aktívan kontrollált eset? Ehhez nem kellene előre jósolnunk, csak megfelelő mértékben kellene reagálnunk az aktuális szituációra.
Nézzük meg ezt a lehetőséget. Feltételezzük, hogy zéró fertőzött esetén az a ráta érvényes, amit a járvány kirobbanásakor Kínában lehetett mérni (kb. R0 = 2,5), az egészségügyi rendszer befogadóképességét (szaggatott vonal) elérő betegszám esetén pedig a rátát a legalacsonyabbnak vesszük, ami tovább már nem csökkenhet. A két szélső érték között lineáris kapcsolatot tételezünk fel, amiben az aktuális ráta csak az aktuális betegszám függvénye (a korábbi cikkben I(t)). Ha azt szeretnénk, hogy ne haladjuk túl a kórházak terhelhetőségét, akkor azt kapjuk (lásd középső ábra), hogy a minimális rátának Rmin = 1,1 -nek kell lennie, tehát önszántunkból jobban kellene korlátoznunk magunkat, mint az aktívan központilag kontrollált esetben, mert ott 1,18 volt a minimális ráta (lásd R1 értékét a táblázat sötétszürke cellájában). Ezen kívül a fenti ábrákból azt is leolvashatjuk, hogy ebben az önszabályozós modellben a lakosságnak csak 53 százaléka fertőződne át, ami sajnos még nem lenne elég a nyájimmunitás teljes kialakulásához és a második hullám elkerüléséhez.
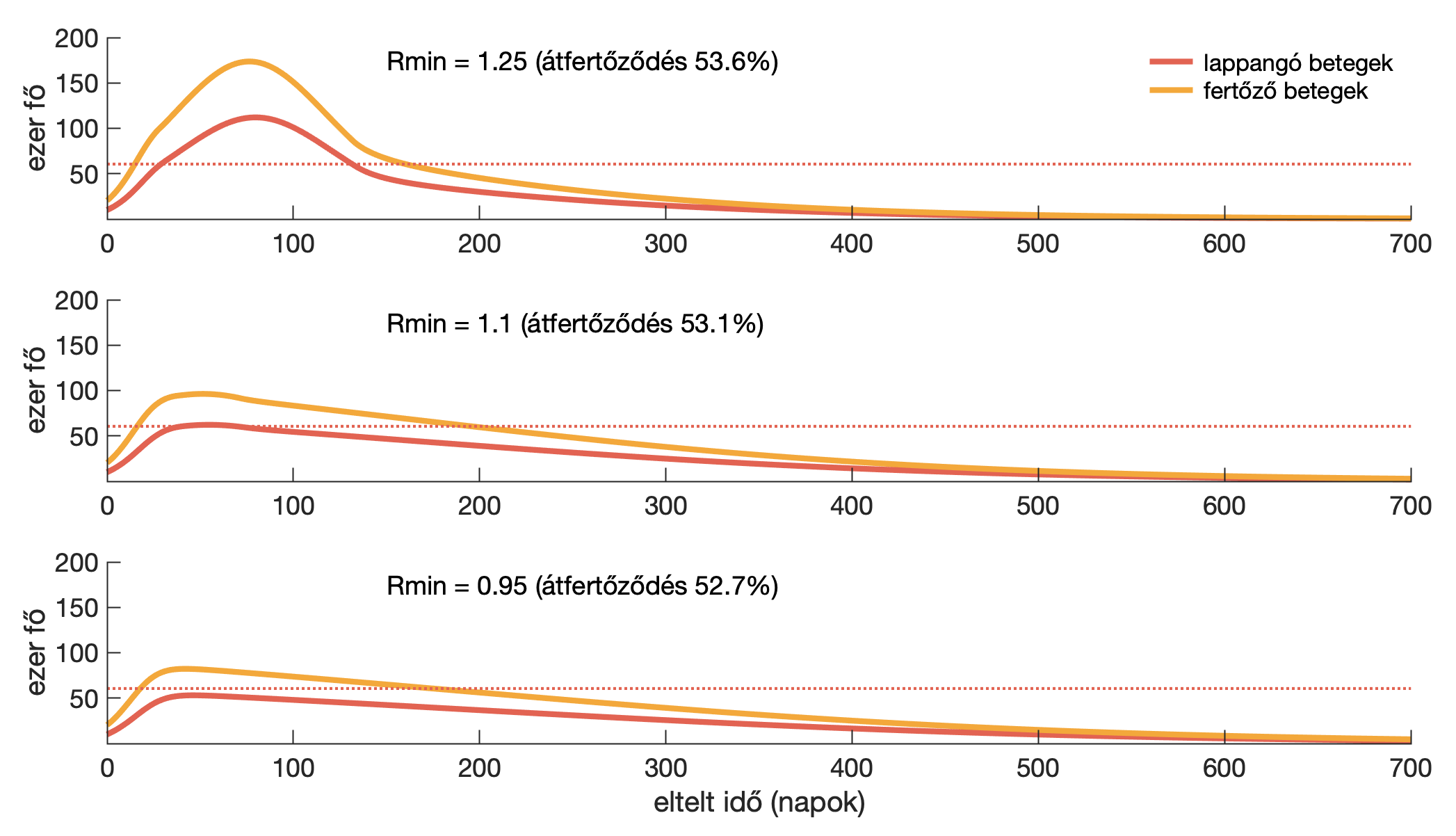
Ez a forgatókönyv akkor is így alakulna, ha nem egyéni önszabályozással, hanem olyan központi rendelkezésekkel oldanánk meg, amiket a döntéshozók nem jóslatokra alapoznának, hanem mindig az aktuális szituációra hagyatkoznának. Fontos tehát, hogy minél jobb modellekkel minél jobb előrejelzéseket tehessünk, ehhez pedig minél pontosabb felmérésekre is szükség lenne.
A koronavírus-járvánnyal kapcsolatos tudományos eredmények bemutatását a Dataizmus Zrt. támogatta.
Kapcsolódó cikkek a Qubiten:
Meddig bénítja meg a világot a járvány, és lesz-e Magyarországon is második hullám?
Hogy nem túl rózsásak a kilátásaink a koronavírus elleni küzdelemben, az nem kifejezés: ha nem sikerül kifejleszteni a vakcinát a SARS-CoV-2 ellen, és a nyájimmunitás sem alakul ki, még sokáig velünk élő járványügyi intézkedésekkel kell számolnunk a hétköznapjainkban.
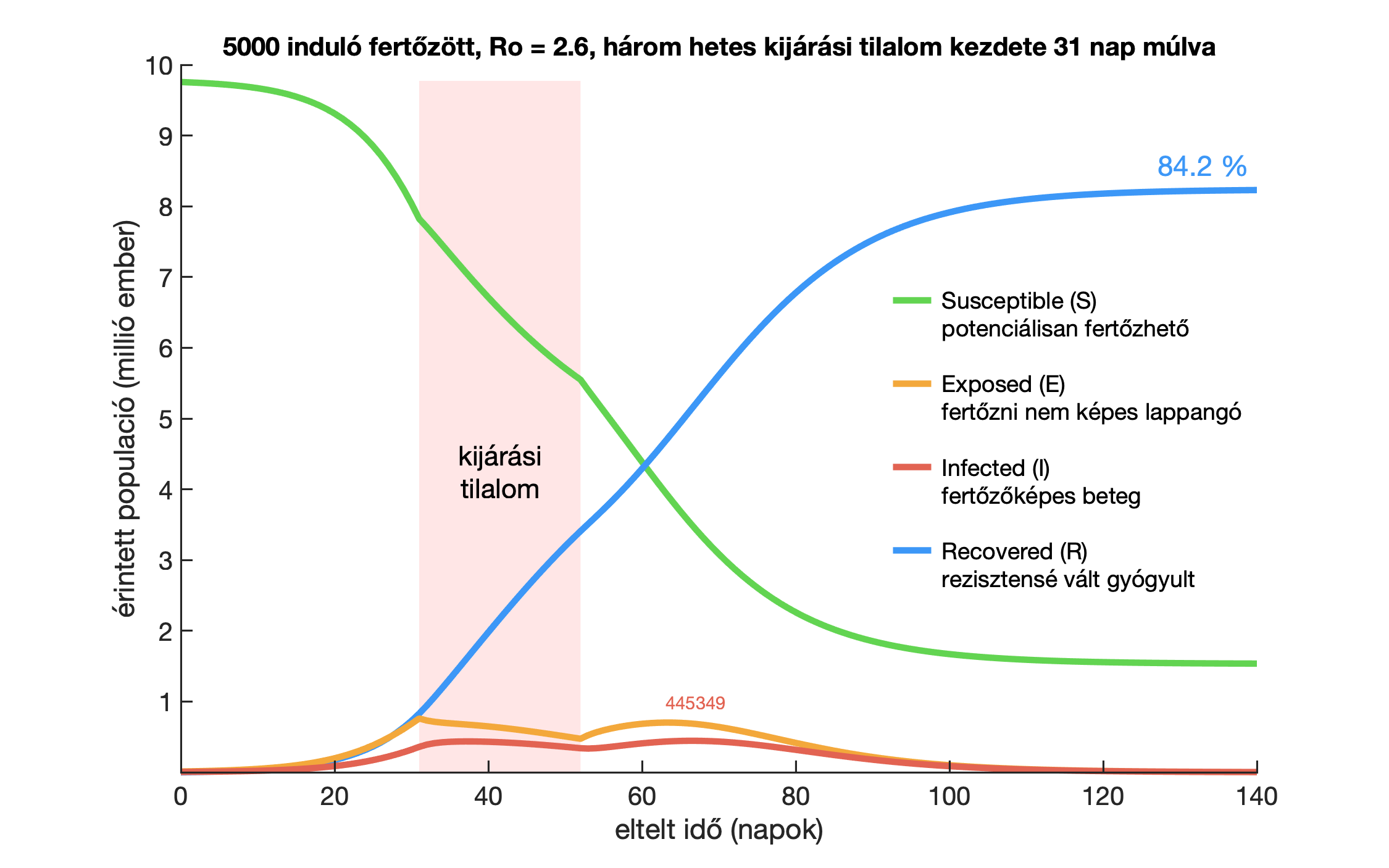
Mikor és mennyi időre érdemes bevezetni a kijárási tilalmat Magyarországon?
Európában eddig több ország, köztük Franciaország, Lengyelország, Nagy-Britannia, Olaszország és Spanyolország rendelt el kötelező karantént. És itthon mi a helyzet? A járványdinamikában használt SEIR modell segít meghatározni a lakhelyelhagyási tilalom bevezetésének optimális időpontját.
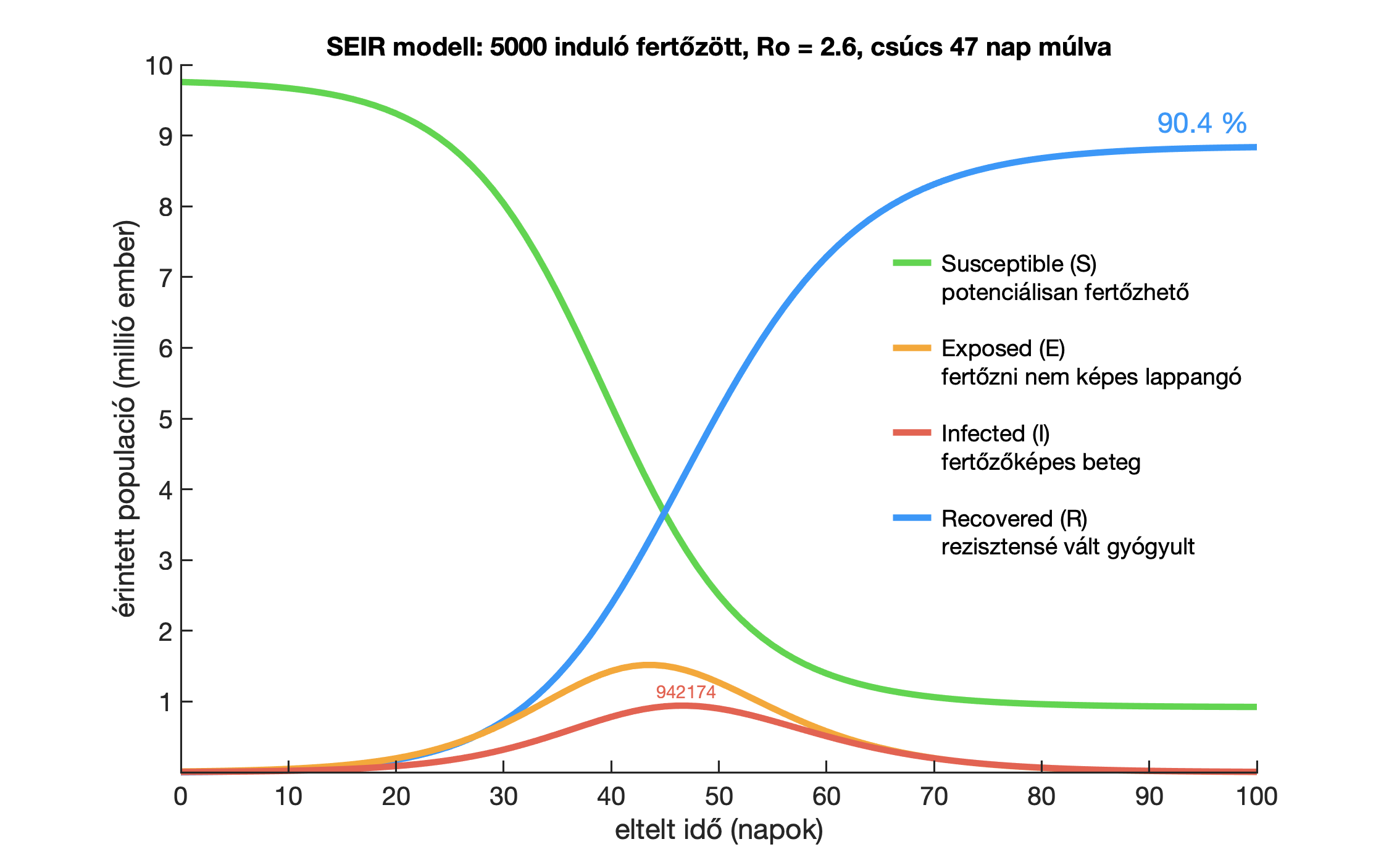
Milyen messze van a járvány csúcsa Magyarországon, és hogyan tudjuk ezt modellezni?
A SEIR modell a fertőzésre fogékonyak, a fertőzöttek és a betegek száma mellett figyelembe veszi a lappangó eseteket is. Az eredmény attól függ, hogy ebben a pillanatban hány fertőzött van az országban, és mennyi az R0, vagyis a reprodukciós ráta.
Kapcsolódó cikkek