Meddig bénítja meg a világot a járvány, és lesz-e Magyarországon is második hullám?

Járványdinamikai cikksorozatom első cikkében ismertettem a SEIR járványdinamikai modellt, és segítségével azt a kérdést jártam körbe, hogy milyen messze lehet még a járvány tetőzése. A második cikkben egy szigorú kijárási tilalom lehetséges hatásait mutattam be. Tegyük azonban most egy kicsit félre azt a kérdést, hogy mikor tetőzhet a járvány, és hogyan vészeljük át a legsúlyosabb szakaszát, amikor a legtöbben szorulnak majd egyszerre kórházi ellátásra, és tekintsünk egy kicsit előrébb. Ebben a cikkben azt szeretném körbejárni, hogy mire számíthatunk hosszú távon az új koronavírussal kapcsolatban, meddig béníthatja még jelentős mértékben az életünket. Számíthatunk-e például második hullámra?
Az új koronavírus, akárcsak az influenza vagy a korábbi koronavírusok, a SARS-CoV és a MERS-CoV, nagy valószínűséggel örökre itt marad velünk. Számos kutatócsoport dolgozik azon, hogy mihamarabb legyen oltóanyag, de ennek a sikere nem garantált: a SARS és a MERS ellen máig nem tudtak oltást kifejleszteni, bár az is igaz, hogy annak kutatásán sokkal kevesebben dolgoztak, mint most a SARS-CoV-2 ellenszerén.
Ha sikerülne is, annak szokásos bevezetése akár másfél év is lehetne, ezt lerövidíteni és az előírt protokollokat kihagyni kockázatos, ugyanakkor a vírus közben tovább is mutálódhat, aminek a lehetőségét sajnos fokozza a hatalmas fertőzésszám. Az ENSZ egészségügyi szervezete, a WHO szerint abban sem lehet igazán bízni, hogy a nyár megfékezné a vírust.
Egyetlen fertőzött elég lenne ahhoz, hogy újrainduljon a járvány
Az a baj, hogy ha egy ország teljesen meg is tudná állítani a járványt, és meggyógyulna az utolsó fertőzött is az országban, amíg a világ más részein jelen van a vírus, ez nem lenne végleges megoldás. Elég lenne egyetlen beutazó lappangó fertőzött ahhoz, hogy beindítsa a járvány második hullámát, ahogy az most Kínában éppen történik. Egy ilyen eset elkerülése érdekében újra le kellene zárni a határokat, és nagyon szigorú belépési szabályokat is életbe kéne léptetni, lehetőleg gyors teszteléssel – jelenleg a leggyorsabb tesztek két és fél órásak –, aminek az eredményét a belépőknek elkülönítőben kellene megvárniuk, és mindezt nyomon követéssel is ki kellene egészíteni. Ugyanakkor még ez sem lenne tökéletes módszer, mert egyetlen tesztnek sem 100 százalékos a hatásfoka.
Az embereket ezért hosszú távon csakis két dolog védheti meg praktikusan: a vakcina, ami mesterséges immunitást ad, vagy a környezetükben élő emberek természetes úton szerzett immunitása. Ez utóbbi mechanizmust hívják nyájimmunitásnak. Ez azt jelenti, hogy amennyiben a populáció jelentős része már átesett a fertőzésen, és ezáltal immunitást szerzett, ez közvetett módon azokat is védi, akik még nem estek át a betegségen, mert jelentősen tudja csillapítani a járvány terjedését, konkrétan 1-es érték alá tudja vinni a reprodukciós rátát azáltal, hogy az immunisak találkozásaikkal nem tudják közvetíteni a vírust. Természetesen nem tudjuk, hogy az immunitás mennyi időre szól, de a vakcinán kívül lényegében csak ez a reményünk. Ha vakcina sincs és a nyájimmunitás sem alakul ki, még sokáig velünk élő járványügyi intézkedésekkel kell számolnunk a hétköznapjainkban.
Hogyan lesz sok emberből nyáj?
Az alábbiakban azzal foglalkozunk, hogy a lakosság mekkora részének kell átfertőződnie ahhoz, hogy életbe lépjen a nyájimmunitás, és az esetleges új gócpontok ne kezdjenek el exponenciális mértékben terjedni, ami a járvány új hullámát okozhatná. A kérdést a korábban már ismertetett SEIR járványmodell segítségével vizsgáljuk meg. Fontos leszögezni, hogy itt két dolog feszül egymásnak: ha az első hullámot annyira letörjük, hogy az egészségügyi rendszerünk bírja a terhelést – ami nyilván célunk –, azzal egyúttal a lakosság átfertőződése is kisebb lesz, és ezért nagyobb valószínűséggel jön egy második hullám. Ezt fogjuk kvalitatíve is megvizsgálni.
Induljunk ki abból, hogy jelenleg Magyarországon van 2650 lélegeztetőgép. Bár sajnos személyzet nélkül ezek nem érnek semmit, legyünk optimisták, és tegyük fel, hogy a tetőzésig ezt vásárlással vagy gyártással (lásd például 3D nyomtatás) mondjuk 3000-re tudjuk bővíteni, és személyzet is lesz a gépekhez. A jelenlegi legáltalánosabb becslés szerint a betegek 5 százalékának lesz szüksége intenzív kórházi ellátásra, ami azt jelenti, hogy a betegszám egyetlen időpillanatban sem mehetne 60 000 fölé, mert akkor lenne olyan, akit nem tudunk ellátni.
A tetőzéskori betegszám lényegében csak R0-tól, a reprodukciós rátától függ, amit befolyásolni tudunk (lásd korábbi cikkünket). Az alábbi táblázat különféle paraméterkombinációkra tartalmazza a SEIR modellnek a járványra és annak tetőzésére jósolt legfontosabb paramétereit (bővebben lásd a szerző blogján). Az oszlopok különböző R0 értékekhez tartoznak, és az oszlopok alatti piros szám mutatja az egyszerre fertőzöttek maximális számát, a kék százalék pedig azt, hogy a lakosságnak mekkora része esik át a fertőzésen a járvány első hullámának végéig. Kiolvasható, hogy az R0 értékét legalább 1,2-re kellene tartósan leszorítani (az 1,3-as érték az influenzaszerű terjedésnek felel meg), hogy a kórházi ellátásunk bírja a terhelést, és ilyen R0-al számolva a lakosságnak 31 százaléka esne át a betegségen.

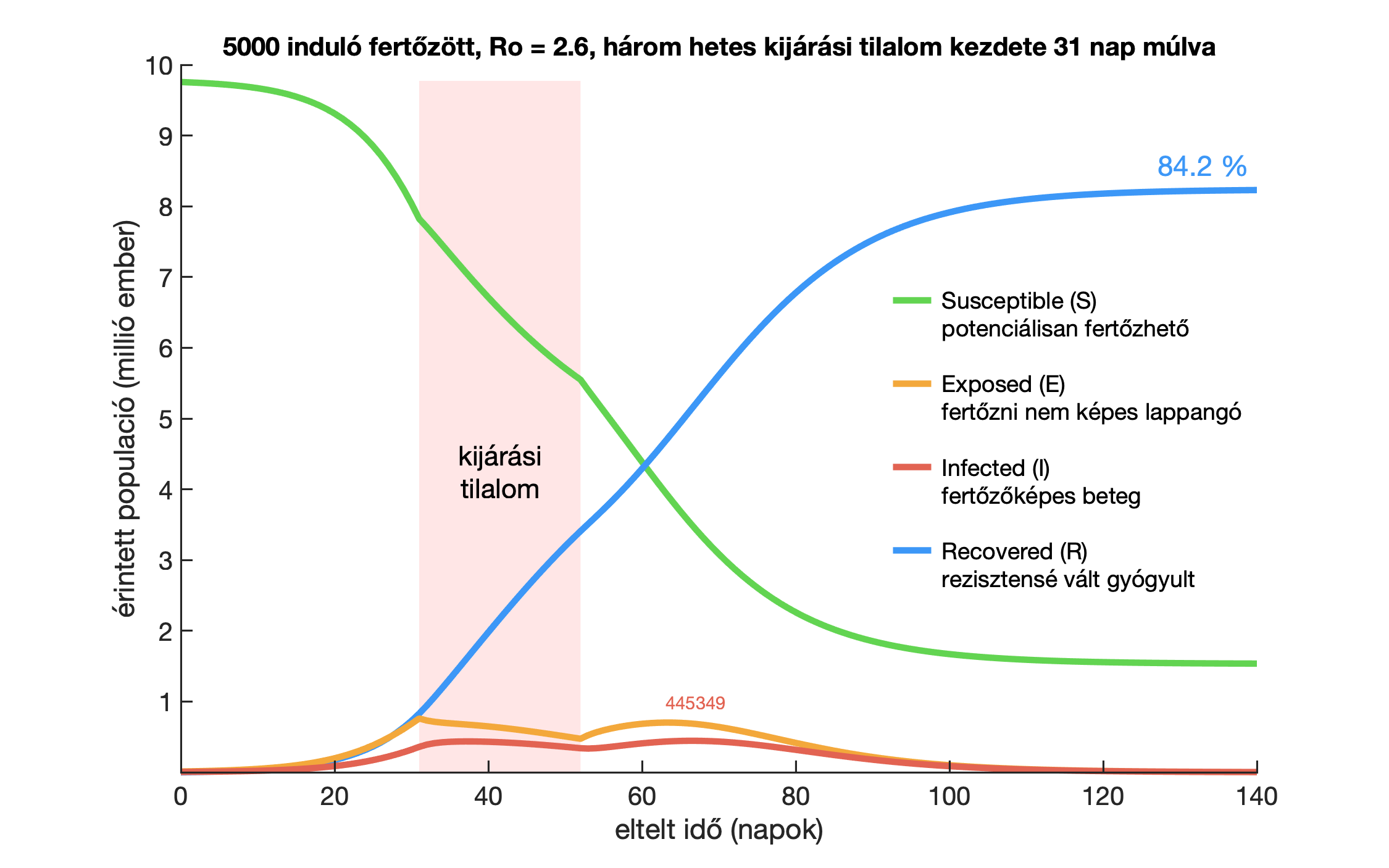
Nézzük most meg, hogy nyájimmunitás szempontjából mire elegendő ez a 31 százalékos átfertőződés. Tegyük fel, hogy a járvány lecseng, és már egy fertőzött sincs az országban, de a lakosság 31 százaléka már immunis. Ők nem tudnak megbetegedni, és nem tudják közvetíteni a fertőzést egy későbbi járvány kialakulása esetén. Tegyük fel, hogy úgy látszik: a veszély elmúlt, ezért visszatérünk a régi kerékvágásba, de a világ más részéből tíz lappangó fertőzött (például két hazatérő magyar család) bejut az országba, és általuk újra elkezd terjedni a vírus. Mivel már nincsenek korlátozó intézkedések, ezért azzal az átlagos R0 = 2,6 -os terjedési rátával számolunk, ami Kínában is mérhető volt a járvány elején. Szimulációnk szerint ekkor ilyen lesz a járvány második hulláma:
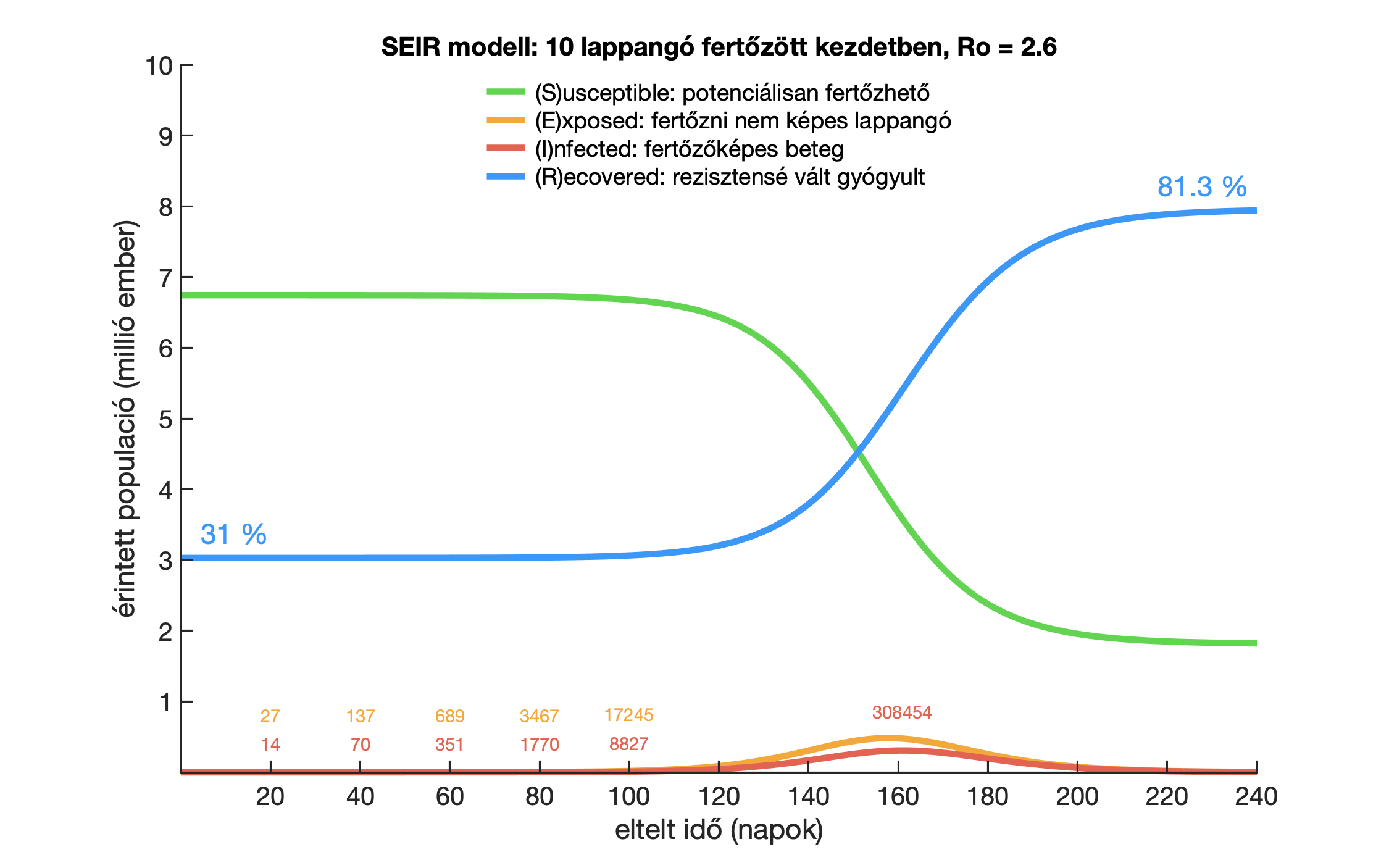
Ha tehát nem tartjuk fenn a járvány lecsengése után továbbra is a készenléti állapotot, akkor a járvány újult erővel és még nagyobb intenzitással tud visszatérni: a járvány első hullámának tetőzésekor feltételezett 60 ezer fertőzött helyett a második hullámban már 300 ezer fertőzöttünk lenne. Ebben természetesen most benne volt az a feltételezés, hogy mindezt ölbe tett kézzel nézzük. Ha megint elkezdjük intézkedésekkel korlátozni a szociális interakciókat, akkor persze képesek lehetünk kordában tartani a járvány második hullámát. Ehhez további segítség lehet, amit az ábráról is leolvashatunk, hogy a második hullám nagyon elnyúlt, csak nagyon lassan indul be, ezért van idő arra, hogy intenzív kontaktkutatással és teszteléssel akár meg is állítsuk. Az ábrán lévő piros számok mutatják a fertőzöttek alakulását az időben (a narancs számok a lappangókat mutatják): 3 hét alatt nagyjából 50 fertőzött, 6 hét alatt 200. Ezek még kezelhető esetszámok lennének kontaktkutatáshoz, ha komolyan vesszük.
Azt látjuk tehát, hogy vakcina hiányában a koronavírus még nagyon sokáig, akár évekig is problémát tud okozni az egész világon. Összefoglalva ennek alapvetően az alábbi okai vannak:
- a vírus kellemetlen tulajdonságai járványügyi szempontból: hosszú lappangási idő, magas reprodukciós ráta, az egészségügyet megterhelő intenzív ellátásra szorulók aránya és a jelentős halálozási ráta;
- hatalmas embertömegek viszonylag szabad mozgása világszerte, ahogyan azt idáig megszokhattuk.
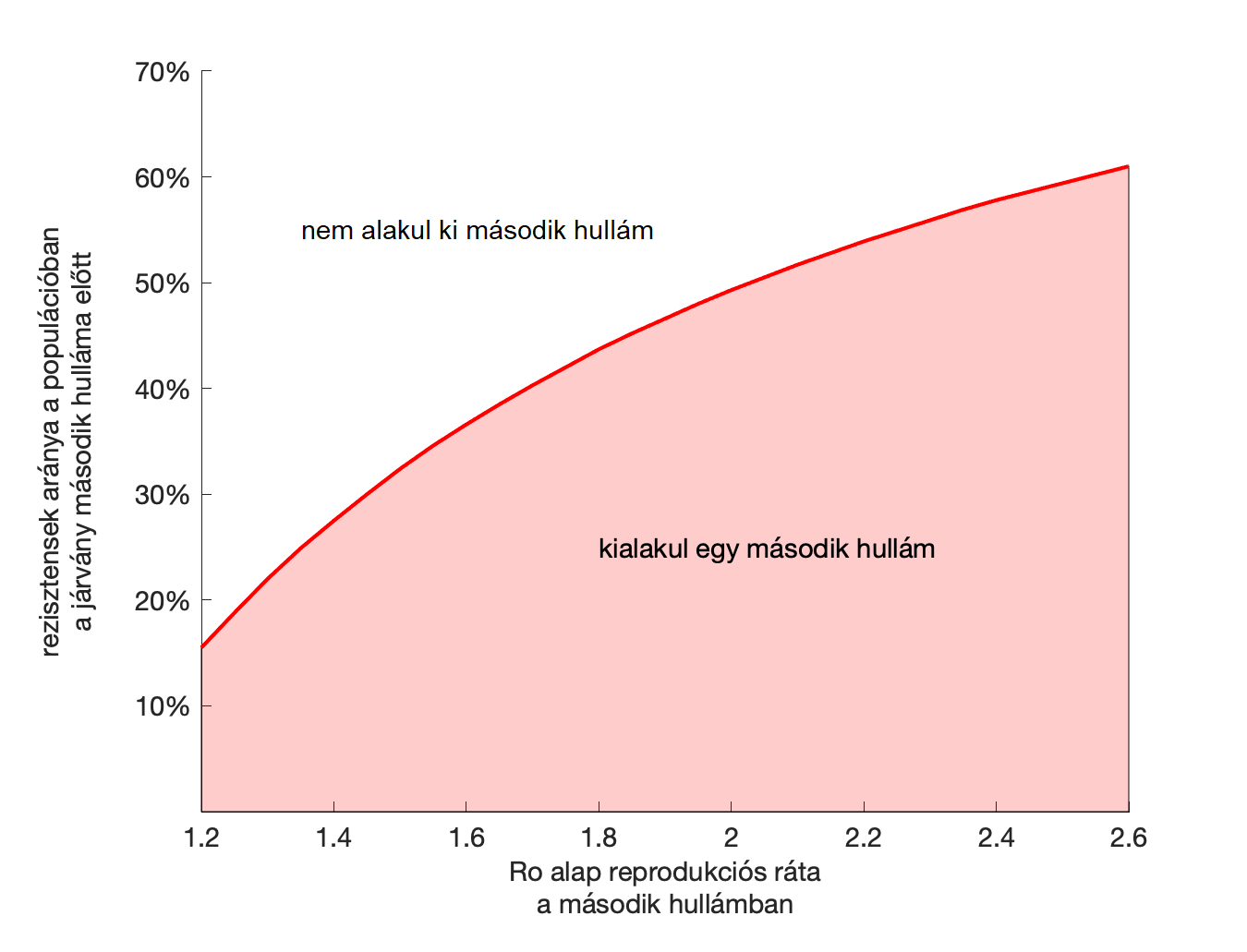
Az érdekesség kedvéért nézzük még meg azt, hogy mik a tulajdonságai a második hullámnak különféle paraméterkombinációk esetére. A szimuláció az R0 rátától, a kezdeti esetszámtól és a rezisztensek arányától függ érzékenyen. A kezdeti esetszámot most fixen tartjuk (ez nagyobb R0-k esetében csak eltolja a csúcsot, de annak magasságát nem befolyásolja lényegesen), ezért R0 és az átfertőzöttek százalékának függvényében nézzük meg a járvány második hullámának tulajdonságait: intenzitás és további átfertőződés mértéke. Az eredményeket az alábbi táblázatban foglaltuk össze, lásd az ábra aláírását az értelmezéshez:
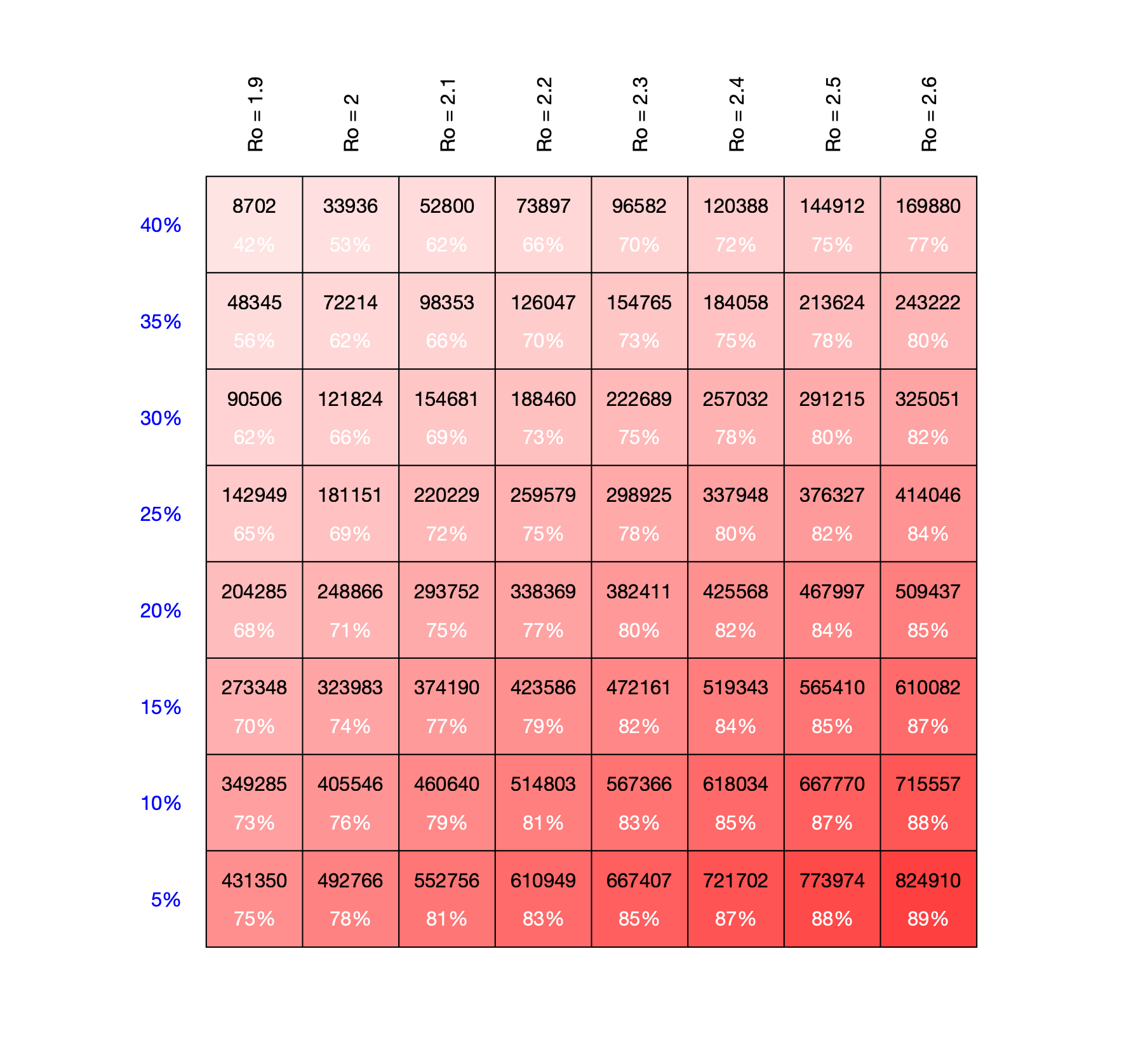
Látható, hogy ha a populáció 40 százaléka már rezisztens és az R0 = 1.9, akkor a második hullám már a populációnak csak a 2 százalékát érinti. Ha a rezisztensek számát tovább növeljük, vagy az R0-t csökkentjük, akkor a járvány második hulláma már nem fog kialakulni, mert az effektív ráta az immunisok miatt 1-nél kisebb lesz, ezért nem alakul ki exponenciális növekedés, tehát a járvány magától elhal. Hogy adott R0 esetén ez hány százalék rezisztensnél következik be, az látható az utolsó ábránkon.
A fenti szimulációk természetesen csak a folyamatok érzékeltetésére szolgálnak, nem konkrét jóslatokra. A folytonos SEIR modell kis esetszámnál a járvány elején nem jól használható konkrét számok jóslására, mert a terjedés véletlenszerű folyamat. A járvány csúcsa ezért eltolódhat az ábrákhoz képest, de a tetőzés mértékét a modell viszonylag jól tudja leírni, ha a paraméterek jól vannak beállítva. Sok azonban a bizonytalan tényező a paramétereket illetően is, például az említett kórházi ellátásra szorulók aránya, amit 5 százaléknak vettünk. Ha sokkal többen esnek át a járványon enyhe tünetekkel, mint amiről tudunk, akkor lehet, hogy sokkal többen váltak immunissá, mint feltételeztük, de az is lehet, hogy az immunitás rövid időre szól, és akkor meg rosszabb a helyzet, mint gondolnánk. Az új koronavírus elleni vakcina fejlesztésére fordított minden erőfeszítés tehát rendkívül fontos a jelenlegi helyzetben.
Kapcsolódó cikkek a Qubiten:
Mikor és mennyi időre érdemes bevezetni a kijárási tilalmat Magyarországon?
Európában eddig több ország, köztük Franciaország, Lengyelország, Nagy-Britannia, Olaszország és Spanyolország rendelt el kötelező karantént. És itthon mi a helyzet? A járványdinamikában használt SEIR modell segít meghatározni a lakhelyelhagyási tilalom bevezetésének optimális időpontját.
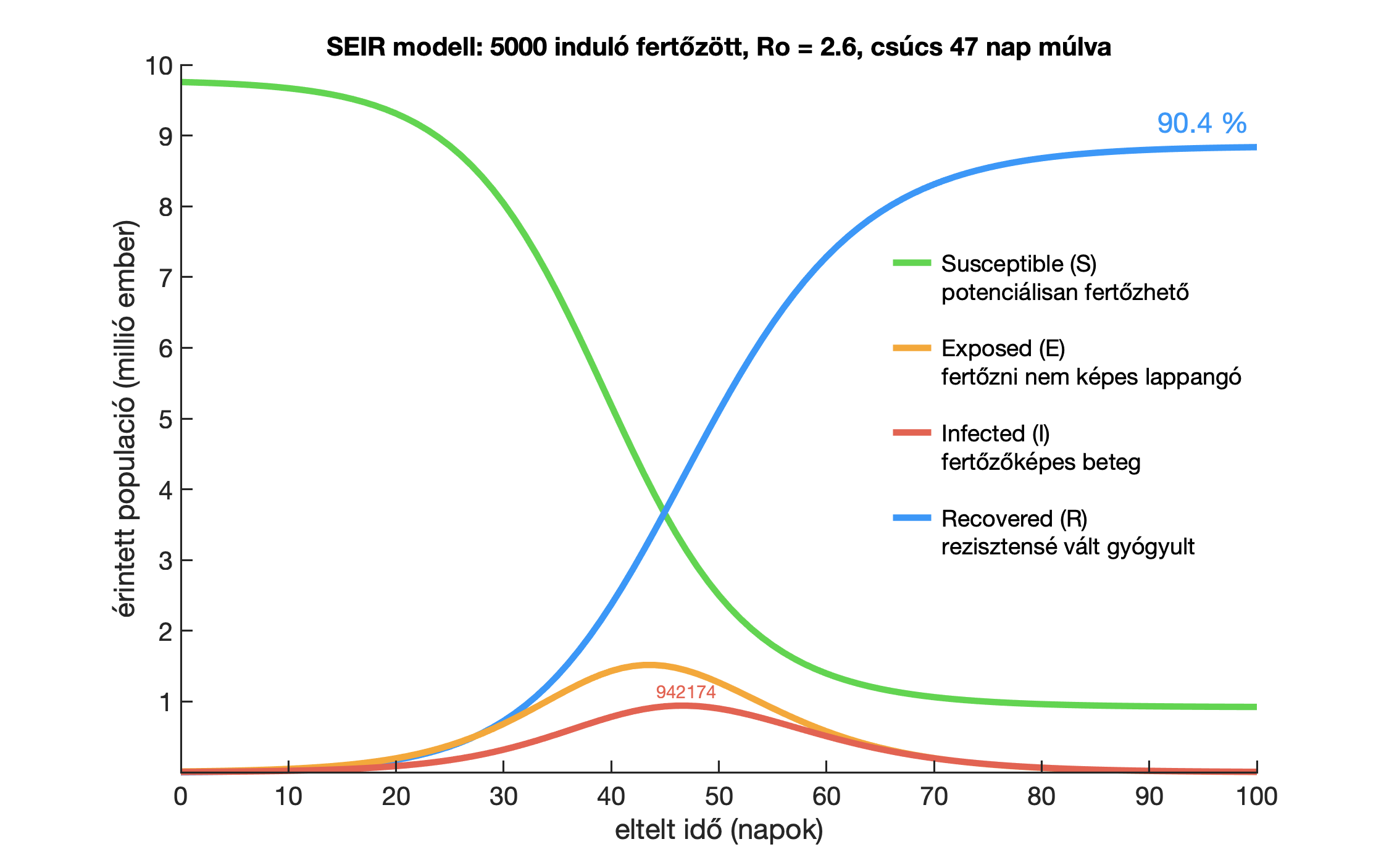
Milyen messze van a járvány csúcsa Magyarországon, és hogyan tudjuk ezt modellezni?
A SEIR modell a fertőzésre fogékonyak, a fertőzöttek és a betegek száma mellett figyelembe veszi a lappangó eseteket is. Az eredmény attól függ, hogy ebben a pillanatban hány fertőzött van az országban, és mennyi az R0, vagyis a reprodukciós ráta.
Kapcsolódó cikkek

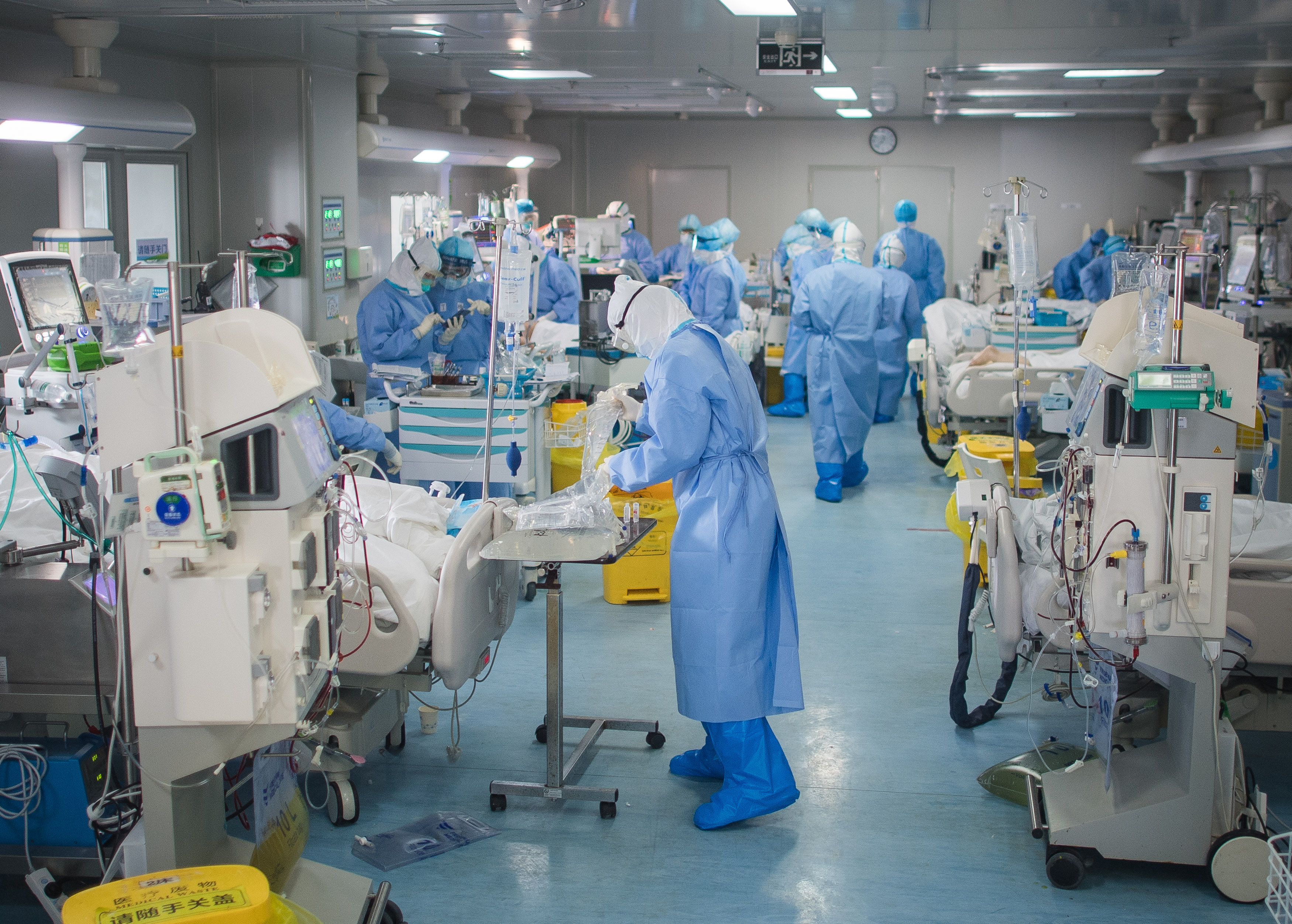



A SARS-CoV és a MERS-CoV ellen máig nem sikerült kifejleszteni a vakcinát. Mi lesz a SARS-CoV-2-vel?