Aki megérti az exponenciális növekedést, nagyobb eséllyel fogadja el a járványügyi intézkedéseket

Az exponenciális növekedést nem értjük: túl gyors a képzeletünknek, és számolni sem kényelmes (sőt kimondottan macerás). Pedig exponenciális növekedéssel az életünk során elég sokat kell foglalkoznunk még járványmentes időkben is. Járványos időkben pedig különösen nem árt ismerni, mit jelent az exponenciális felfutás és az exponenciális lecsengés. Ha az elsőt alulbecsüli valaki, akkor meglepődik, milyen gyorsan nőnek az esetszámok, míg a lecsengésnél a várakozáshoz képes gyorsabb lehet a csökkenés – erősítve azt a hamis képet, hogy nem is volt itt járvány.
Az exponenciális növekedéssel kell dolgoznunk, amikor például kamatos kamatot számolunk. Gyakran találkozhatunk azzal a kérdéssel, hogy ha van 1000 forintom, és kapok rá 5 százalék kamatot (ez példa, nem kapunk ekkora kamatot), akkor mondjuk 5 vagy 10 év múlva mennyi lesz a kamatos kamat.
Az emberek 90 százaléka bizonyítottan alulbecsüli az exponenciális növekedés mértékét. A Kölni Egyetem 2009-es kísérletében részt vevő főiskolai hallgatók negyede hozzá se tudott kezdeni a feladathoz. A legtöbben (35 százalék) egyszerűen lineáris növekedéssel számolnak, vagyis az 5 százalékot megszorozzák az évek számával. A példánál maradva így 10 év alatt 50 százalékkal nőne a pénzük, kamatos kamattal viszont 62,8 százalék növekedést érnének el. A helyes eredményhez közel becslők a lineáris becsléshez hozzáadtak még valamennyit, mert az exponenciális növekedés gyorsabb. Voltak, akik megfelelő képletet alkalmaztak, de túl sok évre előre elég nehézkes a számolás, így a tévedés lehetősége is nagyobb volt. A kölni kísérletéhez hasonló eredmények több más tanulmányban előjöttek.
Járványos időkben az exponenciális felfutás alulbecslése (is) vezethet a hamis biztonságérzethez, ami alacsony esetszámoknál jelentkezik, és hozzájárulhat a bevezetett járványügyi intézkedések elutasításához.

A matematikai ismeretek és a járványügyi intézkedések megítélése
Az amerikai tudományos akadémia lapjában (PNAS) nemrég megjelent tanulmányban a Kölni és a Brémai Egyetem kutatói arra keresték a választ, hogy az exponenciális növekedés meg nem értése mennyire befolyásolhatja a járványkezelési intézkedésekről való gondolkodást. A vizsgálatokat 2020 márciusában végezték.
Az első kísérletben a résztvevőknek megmondták, hogy március 22-én 33546 fertőzött volt az Egyesült Államokban, és ennek alapján kellett megbecsülniük, hogy az előző 5 napban mennyi volt a fertőzöttek száma. Nem meglepően a legtöbben lineáris növekedést feltételeztek – amelynek az üteme lényegesen lassabb volt a ténylegesnél. Nagyon kevesen gondolkodtak exponenciális növekedésben, és ők is alulbecsülték a növekedés mértékét.
A következő kísérletben az új alanyokat két csoportra bontották, az egyik csoporttal a fenti kísérletet végezték el annyi különbséggel, hogy a március 24-ei 54935 esetből kellett visszafele becsülni, míg a többieket a becslés előtt a következő figyelmeztetéssel látták el:
Kérem, figyeljen arra, hogy sok ember elfelejti, a koronavírus terjedésének sebessége mindennap nő. Más szavakkal: amikor többen hibásan becsülnek, úgy gondolják, hogy a koronavírusos esetek száma egyenletes, változatlan ütemben növekszik. A valóságban az Egyesült Államokban, ahogy majdnem minden más országban, a koronavírusos páciensek száma háromnaponta megkétszereződik.
A figyelmeztetés segítette a válaszadók becslésének pontosságát, emellett a csoport tagjai jóval nagyobb arányban nyilatkoztak úgy egy kérdőívben, hogy támogatják a távolságtartásra felszólító intézkedéseket, mint a kontrollcsoportba tartozók. (Hozzáteszem, hogy kétszerezni egyszerűbb, mint mondjuk 1,05-tel szorozni, ami az 5 százalékos növekedés kiszámolásához szükséges.)
Az exponenciális növekedés és hatásának megértetése végett egy harmadik kísérletben nem a múlt eseményeinek becslését, hanem a közeljövőben várható változás becslését kérték a kísérlet alanyaitól. Megadták az információt, hogy minden 3 napban megkétszereződik a betegek száma, majd 3 napos időközönként a következő 15 napra kellett becslést adni. Ebben az esetben egyértelmű(bb) volt, hogy a kezdeti értéket többször meg kell duplázni, és így a kísérletbe bevont válaszadók már sikeresebben vették az akadályt egy exponenciális folyamat becslésére. A március 24-ei érték és háromnapos megkétszereződés mellett két héttel később 1,75 millió beteg lenne. Szerencsére akkor már az Egyesült Államokban sem dühöngött teljesen szabadon a járvány, így két hét múlva, április 9-én „csak” 477766 ismert koronavírusos fertőzött volt, az 1,75 milliós esetszámot pedig május 27-én lépték túl.
A járvány elején, a mostani esetszámokhoz képest még több nagyságrenddel alacsonyabb fertőzésszámnál a megfertőzöttek száma exponenciálisan növekedett. Ahol távolságtartó intézkedéseket vezettek be, ott a járvány terjedése megállítható volt. Amennyiben az emberek betartják az intézkedéseket, a helyzet javul, és minél inkább betartják, annál gyorsabban.
Amikor a napi adatokat nézzük, ne azt lássuk, hogy mennyivel van több eset a tegnapi helyzethez képest, mert hajlamosak leszünk ezt a különbséget kivetíteni a következő hetekre. Azt nézzük, hogy hányszorosára növekedett az esetszám. Ezzel a szorzóval kell továbbszámolni, ha meg szeretnénk becsülni, mi várna ránk, ha minden maradna úgy, ahogy van.
A szerző biológus kutató.
Kapcsolódó cikkek a Qubiten:

Magyarországon a járványt maguk az emberek állították meg azzal, hogy betartották a korlátozásokat
A megfelelő járványügyi korlátozások után mindenki azt fogja érezni, hogy túlzók voltak az intézkedések. De ha az ország újranyitása után továbbra is próbáljuk minimalizálni kapcsolatainkat, elkerülhető egy gyorsan kialakuló második hullám. Ahogy az eddigi siker, ez is rajtunk múlik.

Helyes volt-e feloldani a karantént Magyarországon úgy, hogy több fertőzött volt, mint amikor elrendelték?
Kifejezetten irracionálisnak tűnhet, hogy a járványnak egy látszólag súlyosabb szakaszában feloldjuk azokat a korlátozásokat, amiket a járvány sokkal enyhébb szakaszában vezettünk be. Mi a magyarázat?
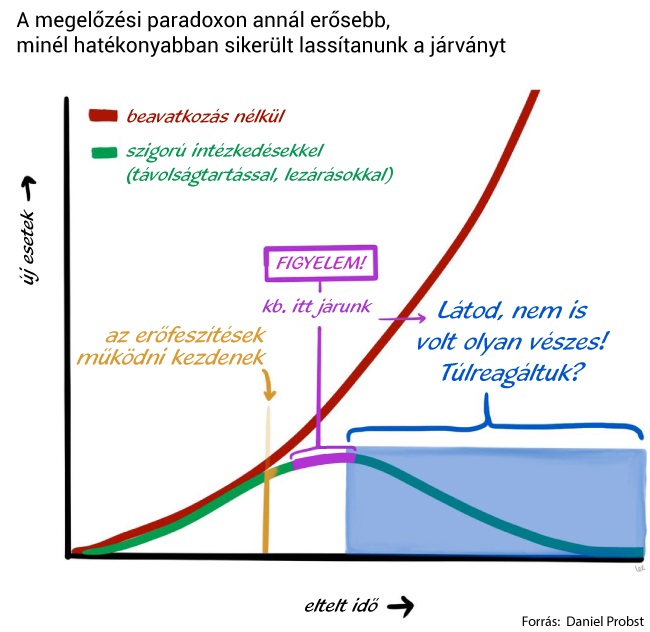
Túlreagáljuk-e a koronavírus-válságot?
Nem tudjuk, hogy minden egyes korlátozó intézkedés hatékonyan járult-e hozzá ahhoz, hogy a vírus ne duplázódva terjedjen, és hogy a súlyos esetek száma a legtöbb országban ne haladja meg az egészségügy teljesítőképességét. Az viszont biztos, hogy a sikeres stratégiáktól épp ezeket az eredményeket vártuk.