Magyar kutatók szenzációs felfedezése: kockákra hullik szét a világ
A kubista festők megsejtettek valamit: egy magyar kutatás arra jutott, hogy ami csak szétesik a világban – a jégtömböktől a sziklákig – kockára emlékeztető darabokra hullik. Az amerikai tudományos akadémia folyóiratában, a PNAS-ban július 17-én megjelent tanulmány eredményei arra engednek következtetni, hogy ez a szabály univerzálisan érvényes, a mikroszkopikus világtól egészen a bolygóközi méretekig.
„Csodálatos kombinációja a tiszta matematikának, az anyagtudománynak és a geológiának” – jellemzete a kutatást a Science-nek Sujit Datta, a Princeton Egyetem vegyész- és biomérnöke, aki nem vett részt a tanulmány elkészítésében.
A tanulmány vezető szerzője a gömböcöt kidolgozó szakemberek egyike, Domokos Gábor alkalmazott matematikus, a Budapesti Műszaki és Gazdaságtudományi Egyetem (BME) munkatársa, az eredmények az ő és kutatótársai által jegyzett korábbi kutatásokon alapulnak. A cikk társzerzői Douglas Jerolmack, a Pennsylvaniai Egyetem környezettudományi tanszékének geofizikusa, illetve Kun Ferenc és Török János, a Debreceni Egyetem és a BME elméleti fizikusai.
A gömböc olyan konvex háromdimenziós test, amelynek összesen két egyensúlyi állapota van, és azok közül is csak az egyik stabil. Akárhogy tesszük az asztalra, mindig ugyanazt a pozíciót veszi fel, ellentétben például a hengerrel, amely az oldalán vagy valamelyik végén is megállhat. (Az alábbi videón pedig a gömböc amerikai kiejtését is megcsodálhatjuk.)
Domokos és kollégái a gömböcre épülő későbbi kutatásaikban arra jutottak, hogy a folyó mosta kavicshoz és a szélben szálló homokszemcsékhez hasonló természetes formák eróziója gömböcszerű elemek képződéséhez vezet, ám ezek sose érik el a gömböc végső formáját. Ahogy Domokos fogalmazott: „a gömböc a természet része, de csak mint egy álom”.
Kísérlet az absztrakt kockával
Következő lépésben a Domokos-féle kutatócsoport a folyamat másik oldalát, a kövek képződését kezdte vizsgálni. Három és fél éves kutatásukat azzal kezdték, hogy egy absztrakt kockát számítógépes szimulációban 50 kétdimenziós síkkal szabdalták fel úgy, hogy a síkok véletlenszerű szöget zártak be a kocka lapjaival. Az absztrakt kockát ily módon hatszázezer darabra vágták, amelyek az átlagot tekintve maguk is kockaszerű alakot vettek fel, vagyis a töredékeknek hat négyszög alakú oldaluk volt még úgy is, hogy az egyes daraboknak nem kellett feltétlenül kockának lenniük. Pontosabban fogalmazva ha véletlenszerűen választott síkokkal kellően sokszor vágunk ketté egy testet, akkor a folyamat eredményeként keletkező testek lapjainak, csúcsainak és éleinek átlaga rendre 6-hoz, 8-hoz és 12-höz tart, azaz az „átlagos alakzat” egy kocka lesz.
Ez az eredmény vezette a kutatókat ahhoz az elmélethez, hogy a kockák a szétesés, a töredezés velejárói a természetben is.
Ezt az elméletet a való világban végzett mérésekkel igyekeztek megerősíteni, amihez a budai Hármashatárhegy ásványi dolomitjait használták. Összeszámolták a kőfelület repedéseiben a csúcsokat, és arra jutottak, hogy ezek a repedések többségükben majdnem négyszögletű formákat határolnak, amelyek pedig egy kocka egyik oldalát adják – függetlenül attól, hogy a repedés természetesen vagy emberi beavatkozásra (például bányarobbantás miatt) keletkezett.

Végül a kutatócsoport további, még nagyobb számítási kapacitást igénylő szuperszámítógépes modellezéssel ábrázolta a háromdimenziós anyagok ideális körülmények közötti feltöredezését – ilyen például, amikor egy követ egyenlő erővel valamennyi irányba húznak. Ezek a behatások olyan soklapú testeket (darabkákat) hoztak létre, amelyek nagy átlagban kockáknak mondhatók.
Természetes, de teoretikusan
Igen ám, de a természetes világban számos dolog egyszerűen nem kockákra töredezik: a csillámpala pehelyszerű képződményekre esik szét, a bazaltformációk pedig hatszög alapú hasábokra. Ennek oka, hogy az igazi anyagok nem olyanok, mint a kutatók szimulációban használt ideális alakzatok – magyarázta a tanulmány egyik szerzője, Jerolmack –, és általában olyan belső struktúrákat tartalmaznak vagy olyan tulajdonságokkal bírnak, amelyek nem a felkockázódásnak kedveznek. A pala például azért pelyhekre esik szét, mert az egyik irányban erősebb az anyag, mint az arra merőleges irányban. „Ám a statisztikai átlagot tekintve a kövek képződése olyan formákkal kezdődik, amelyek a kockák homályos, torz árnyékainak tekinthetők.”
Jerolmack szerint eredményeik segíthetnek a hidrológusoknak előrejelezni, hogyan áramlik a folyadék a kőzetrepedésekben, ami jól jön például olajkitermelésnél, illetve támogathatja a geológusok számításait, amikor egy letöréshez közeli szikladarab méretét kell kiszámolniuk.
Van, aki azonban nehezen fogadja be ezt tanulmányt, ilyen kritikát fogalmazott meg például Anne Voigtlander, a GFZ Német Földtudományi Kutatóközpont geológusa: „geológusként nehéz lehet felfogni a kutatás értékét vagy alkalmazhatóságát”.
Platóni inspiráció
Jerolmack is egyetért azzal, hogy bizonyos értelemben az eredményeik inkább filozofikusak, mint tudományosak. A kutatócsoportot Platón elmélete inspirálta ebben a kutatásban, ahogy a tanulmány címe is utal rá: Platón kockája és a töredezés természetes geometriája. Az ókori görög filozófus szerint a világmindenséget alkotó négy elem, a föld, a víz, a tűz és a levegő mindegyike szabályos testekből épül fel, a föld például hexaéderekből, azaz kockákból áll.
Platón barlangi allegóriája azonban jóval ismertebb: ebben bizonyos idealizált és örök formákról elmélkedett, amelyeknek csak közel azonos, „hamis” verziói léteznek a valóságban. Domokos szerint „puszta szemmel csak torzított képeket látunk, a töredékeket. Ahhoz, hogy az ideálist is meglássuk, az elménkkel kell néznünk.” A BME honlapjának pedig úgy összegzett: „Naprendszerünk tele van szüntelenül aprózódó kövekkel és sziklákkal. Mi ezt a folyamatot egy eddig itt nem alkalmazott geometriai szemüvegen, a konvex mozaikok elméletén keresztül figyeltük meg.”
A kutatásnak hála természettudományos értelemben a gömböc is helyére került: azt már korábban bizonyították, hogy a természetben fellelhető testek a kopásuk során folyamatosan veszítik el egyensúlyi helyzeteiket, tehát a gömböc felé közelednek, de ezt a végső állapotot sosem érik el. A mostani kutatás a folyamat elejét jelölte ki azzal, hogy a szintén láthatatlan kockában találta meg a kezdeteket.
Kapcsolódó cikkek a Qubiten:
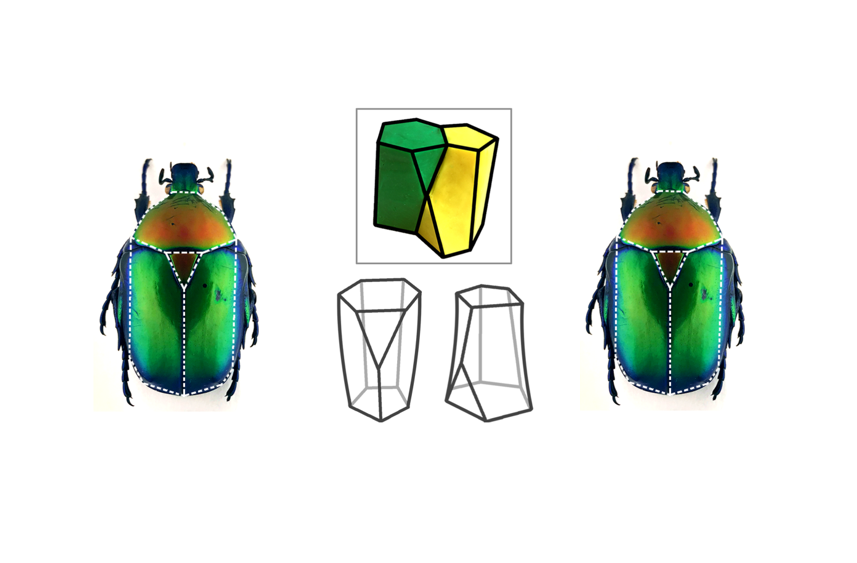
Új geometriai alakzatot fedeztek fel: hello, pajzsoid!
A virágbogárfélék torán található pajzsocskára emlékeztet az a frissen felfedezett alakzat, amely a jövőben a mesterséges belső szervek megalkotásánál is hasznos lehet.

Miért görbül a tér?
Gáspár Merse Előd fizikus végre rendesen elmagyarázza, mire jutott Galilei, Maxwell, Eötvös és Einstein.

Szobrot emeltek a Gömböcnek Budapesten
Az egyetlen stabil és egyetlen instabil egyensúlyi helyzetű geometria alakzat élethű mása a világ első köztéri Gömböc-szobra. 4,5 méter magas, 4 tonnát nyom, és a Corvin Sétányon már megcsodálható.
