Ész Ventura: Bár az ország tesztelése elmaradt, mi azért megoldjuk a feladatot
84. feladványunk még áprilisban született, amikor a tömeges tesztelés fontossága felmerült. Azóta ez a téma, úgy tűnik, a süllyesztőbe került, mi azért egy hipotetikus ország hipotetikus problémáját megpróbáljuk megoldani.
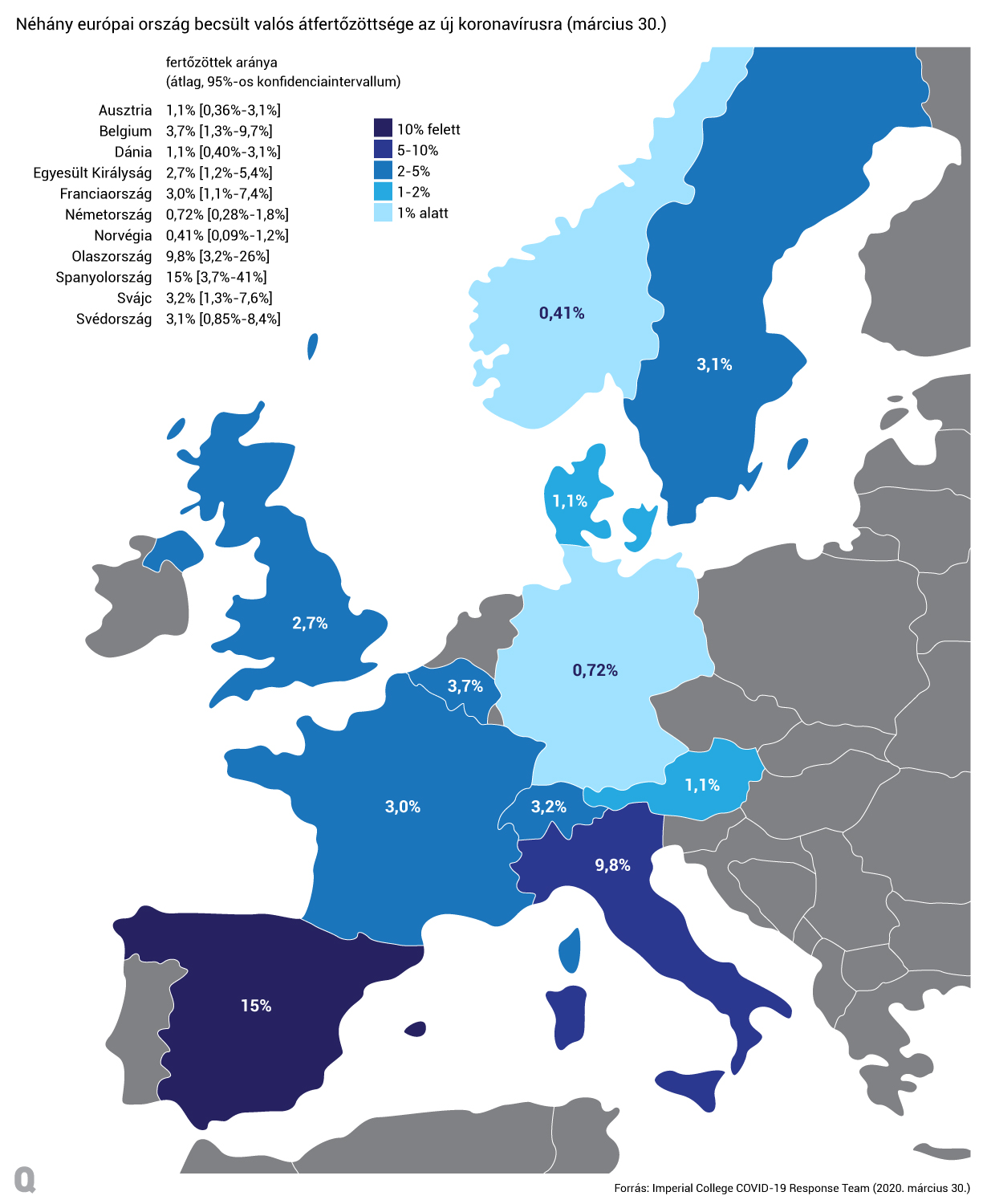
A feladat szerint egy országban járvány dúl, és le szeretnénk tesztelni az összes embert, hogy megtudjuk, pontosan kik a vírushordozók. Egy különleges teszttel már elvégeztek egy előzetes mérést. Ennek során a teljes lakosságot öt fős csoportokba osztották, és az öt fős csoportokban az egyének mintáit összeöntve közös tesztet végeztek minden csoportra. A teszt nemcsak azt állapította meg, hogy az adott csoportban valaki fertőzött-e, hanem az is teljes biztonsággal kiderült belőle, hogy a csoportból pontosan hány fő hordozza a vírust.
N5 = 5000 csoportban mind az 5 fő fertőzött volt, N4 = 6000 csoportban 4 fő, N3 = 7000 csoportban 3 fő, N2 = 8000 csoportban 2 fő, N1 = 9000 csoportban csak 1 fő volt fertőzött. A populáció maradékában nem volt fertőzött.
Ez a különleges teszt azonban elfogyott, és már csak olyan teszt elérhető, darabja 30 dollárért, ami csak azt mondja meg, hogy egy vizsgált mintában van-e fertőzés. A korábbi egyéni minták mindegyikének egy része még megvan, és megengedett, hogy ezeket tetszőleges módon összeöntsük, de csakis csoportokon belül képezhetünk belőlük közös mintákat. Az egyéni mintákat viszont részekre is oszthatjuk, hogy egy-egy fő mintáját több mérésben is használni tudjuk.
A kérdés az, hogy optimális tesztelési stratégia esetén minimum hány dollárba fog kerülni a tesztelés befejezése, ha az összes vírushordozó személyt azonosítani szeretnénk? Bármilyen stratégiát is választunk, számítsunk mindig a legrosszabb lehetőségre, ami előállhat.
Lássuk a megoldást
Egy öt fertőzöttet tartalmazó csoportban mindenki fertőzött, ott nincs szükség további teszteket végezni. Azokkal a csoportokkal kell csak foglalkozni, ahol van egészséges és fertőzött is.
Egy olyan csoportban, ahol pontosan egy fertőzött van, ott öt eset lehetséges arra vonatkozóan, hogy ki a fertőzött. Egy teszt eredménye igen/nem válasszal, azaz 1 bit információval szolgál. Két teszt elvégzésével, azaz két igen/nem kérdés feltételével maximum négy (2×2) különböző eset között tudnánk különbséget tenni, tehát minimum három kérdésre, azaz tesztre szükség lesz. Három teszt viszont a legrosszabb esetben is elég lesz. Először letesztelünk egy embert. Szerencsés esetben megtaláljuk a fertőzöttet, szerencsétlen esetben marad négy fő, akik között egy fertőzött van. Közülük kettőt tesztelünk együtt, majd amelyik kétfős csoportban a fertőzött van, abból a harmadik teszttel egyet, és akármi lesz a teszt eredménye, abból tudni fogjuk, hogy kettejük közül melyik a fertőzött. Tehát az ilyen csoportokban minimum 1, maximum 3 tesztet kell végezünk.
Az olyan csoportokban, ahol három egészséges és két fertőzött van, vagy fordítva, azaz három fertőzött és két egészséges, ott tíz eset (öt alatt a kettő) lehetséges arra vonatkozóan, hogy ki fertőzött és ki nem. Három kérdés feltételével maximum nyolc (2×2×2) különböző eset között tudnánk különbséget tenni, tehát minimum négy kérdésre, azaz tesztre szükség lesz. Négy teszttel viszont könnyedén megvalósítható a feladat, ha az ötből négy embert egyesével letesztelünk. Az ötödikről már egyértelmű lesz, hogy fertőzött-e vagy sem. Két fertőzött esetén akkor leszünk a legszerencsésebbek, ha az első két teszt pozitív, három fertőzött esetén viszont akkor, ha az első kettő negatív. Tehát az ilyen csoportokban minimum 2, maximum 4 tesztet végzünk.
Egy olyan csoportban, ahol négy fertőzött van, nem érdemes keverni a mintákat, hiszen kettő vagy több minta keverése esetén biztosan fertőzött lesz az egész keverék, amiből plusz információt nem nyerhetünk. Itt tehát csak egyesével érdemes mérni, és akkor minimum 1, maximum 4 tesztet kell végeznünk.
Összességében tehát azt kapjuk, hogy optimális tesztelési stratégia esetén a legrosszabb esetben 9000×3 + 8000×4 + 7000×4 + 6000×4 = 110 ezer tesztet kell végeznünk, aminek a költsége 3,33 millió dollár. Ezen kívül azt is megállapíthatjuk, hogy a fenti stratégiával a minimum teszt, amit el kell végezni, ha nagyon szerencsések vagyunk, akkor 9000 + 8000×2 + 7000×2 + 6000 = 38 ezer, aminek a költsége 1,35 millió dollár.
Kapcsolódó cikk a Qubiten:
