100. feladványunk a matematika egy közérthető, de mégis nehéz területét érintette, a köztudott tudás problémáját. Nem mindegy, hogy valaki csak tud valamit, vagy azt is tudja, hogy a másik is tudja róla, hogy tudja. Ahogy az sem mindegy, hogy mindenki tud valamit (közös tudás), vagy mindenki tudja azt is, hogy mindenki tudja, sőt azt is tudja mindenki, hogy mindenki más is tudja mindenkiről, hogy tudja, és így tovább a végtelenségig (köztudott tudás). A hétköznapi életben is számtalan helyen jelentősége van ezeknek a különbségeknek, de erre nem is szoktunk felfigyelni. Erről a problémakörről és hétköznapi példákról egy kitűnő összefoglaló írást olvashattok Pintér Gergő matematikustól az Infosztrájkon.

A köztudott tudással kapcsolatos feladványunkat mesébe burkoltan fogalmaztuk meg. A történet teljes terjedelmében elolvasható az eredeti cikkben, most röviden össszefoglaljuk a feladvány lényegi részét.

A királynak volt 101 egyforma báránya, amelyek közül az egyik az elvarázsolt királylány. A királynak volt négy elkerített legelője és négy őrtornya is. Az észak-keleti őrtoronyból pontosan belátható volt az északi és a keleti legelő, de a másik két legelőre ebből a toronyból egyáltalán nem lehetett rálátni. A délnyugati őrtoronyból viszont a másik két legelő volt látható, és az előbbiek nem. Az északnyugati őrtoronyból belátható volt az északi és a nyugati legelő, de nem látszott a déli és keleti legelő. A délkeleti őrtoronyból pedig látszódtak a déli és keleti legelők, de nem volt rátekintés a másik kettőre.

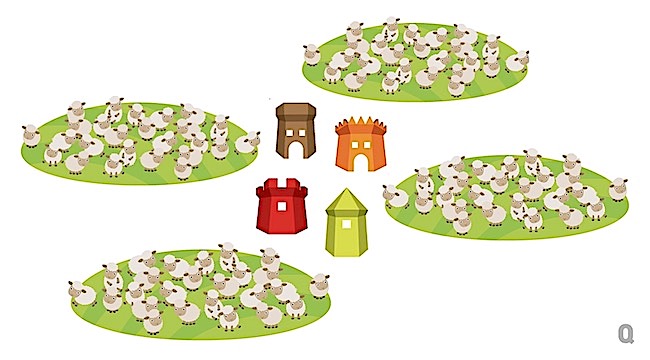
A királyhoz négy okos testvér érkezett, akiknek elmondta, hogy száz báránya van, és még a báránnyá változott lánya, de ő gyakran elcsatangol a többiektől, nem biztos, hogy most a nyájjal van. A király a négy testvért kivezette az őrtornyokba, mindegyiket egy másikba. Aznap minden legelőn pontosan 25 bárány volt, de ezt a testvérek nem tudták, ahogy azt sem, hogy a királylány nincs kint aznap. Mindenki csak két legelőt látott a saját tornyából. Ezután körbejárt a király, és sorban megkérdezte őket, hogy mit gondolnak, kint van-e a királylány aznap a bárányok között, vagy sem? Nem volt kötelező felelni a király kérdésére, de ha valakinek a válasza helytelen lett volna, a király azonnal a fejét véteti mindegyiküknek. A király azonban több lehetőséget is adott, vagyis azonos sorrendben rendre körbejárt az őrtornyok között, és mindig újra és újra megkérdezte a testvéreket egyesével, hogy mit gondolnak.

A testvérek nagyon okosak, sőt egyformán okosak voltak, de a saját vagy a testvérei fejét senki nem akarta kockára tenni. A báránnyá változott királylány vissza tudott volna változni, ha valaki biztosan tudja állítani, hogy a bárányok között, amiket lát, ott van a királylány, vagy azt, hogy biztosan nincs közöttük. Aki pedig képes lett volna megtörni az átkot, az feleségül vehette volna a királylányt. A király úgy okoskodott, hogy ha minden testvér ugyanazt látja és ugyanúgy gondolkodik, akkor egyikőjüknek sem lehet semmi oka arra, hogy a többitől eltérően viselkedjék, így senkié nem lehet a királylány. De nem így történt.

A király az első testvért az északkeleti toronyba küldte, a másodikat a délkeletibe, a harmadikat a délnyugatiba, a negyediket az északnyugatiba. A látogatását az első testvérnél kezdte. Melyik testvéré lett végül a királylány, és hányadik kérdésre felelt meg?

Megjegyzések: a testvérek tudták, hogy elvileg az is lehetséges, hogy valamely területen vagy területeken esetleg egy bárány sincs. A bárányok a király kérdései alatt helyben maradtak. A testvérek azt is pontosan tudták, hogy a többi őrtoronyból mely területek látszanak és ki melyik őrtoronyba került. Továbbá azt is tudták, hogy a király milyen sorrendben látogatja végig a testvéreket (mindig ugyanabban). Ha egy testvér biztosan tudta a választ, akkor válaszolt, és ezt a többiek is tudták róla. Ha nem volt biztos a dolgában, akkor nem válaszolt. A testvérek elég okosak voltak ahhoz, hogy amit tudni lehet, azt tudják is.

Váljon hát közös tudássá a megoldás!

Hogyan tudja az egyik testvér megállapítani, hogy ott van-e a királylány, ha mindig ugyanazt látja, és a király is mindig ugyanazt kérdezi mindenkitől? Mi változik körről körre, honnan származik plusz információ? Nyilván nem abból, amit a testvérek látnak: csak az jelenthet plusz információt valakinek, hogy telik az idő, vagyis az előtte lévők újra és újra nem tudnak válaszolni.

Csakhogy az is hordoz információt, hogy valaki nem tudott válaszolni, mégpedig mindenki számára. Elvileg lehetne olyan eset, azaz a bárányoknak olyan elosztása, hogy valaki rögtön tudjon válaszolni. Ha valaki ugyanis 101 bárányt látna, akkor rögtön válaszolna, abból tehát, hogy valaki nem válaszol, mindenki tudja, hogy nem 101 bárányt lát az illető.

Amikor tehát lemegy az első kör, és senki sem válaszol, mindenki tudni fogja, hogy senki nem látott 101 bárányt. Ezen kívül a szemközti testvérek különös helyzetben vannak, mert ketten együtt látják az egész nyájat, és ezt mindenki tudja róluk, ezért kiderül még valami mindenki számára az első körben. Amikor ugyanis a harmadik testvér nem válaszol, akkor nemcsak az válik nyilvánvalóvá mindenkinek, hogy nem lát 101 bárányt, hanem az is, hogy nem lát nullát. Ha ugyanis nullát látna, mivel ő már tudja (és ezt mindenki tudja is róla), hogy az első testvér maximum 100-at lát, ezért ebből tudná, hogy ketten együtt is maximum 100-at látnak, ami pedig az egész nyáj, tehát tudná, hogy nincs ott a királylány. Hasonló a helyzet a negyedik testvérrel is: abból, hogy ő nem válaszol, a többiek mind tudni fogják nemcsak azt, hogy maximum 100-at lát, de azt is, hogy legalább 1-et, mert tudják róla, hogy tudja ő is, hogy a második testvér nem látott 101-et.

Mármost ha ezt körről körre továbbvisszük, akkor kiderül, hogy rendre minden körben 1-gyel csökken a felső korlátja és 1-el növekszik az alsó korlátja annak a köztudott tudásnak, ami az egyes testvérek által látott bárányok számára vonatkozik. Ha ezt végigkövetjük, kiderül, hogy a király 51. körében a délnyugati őrtoronyban lévő (harmadik) testvér jöhet majd rá arra teljes bizonyossággal, hogy csak 100 bárány van kint a legelőkön, azaz nem látja senki a királylányt. Nézzük pontosan, hogyan jut erre a következtetésre!

A szóban forgó kérdés a 203. kérdés. Ekkor már köztudott tudás lesz, hogy a délkeleti és az északkeleti testvér is legalább 50-et és legfeljebb 50-et, tehát mindketten pontosan 50-et látnak. Mivel pedig a délnyugati, akit éppen kérdez a király, 25-öt lát a déli és 25-öt a nyugati legelőn, most már pontosan meg tudja állapítani, hogy mindegyik legelőn pont 25 bárány van.

Tehát összesen 202 válasz nélkül maradt kérdés után a 203. kérdésre érkezik a helyes válasz. Az pedig, hogy ennél hamarabb nem juthatnak célhoz, következik abból, hogy minden korábbi kérdésnél lehetséges 100 és 101 báránynak is olyan elosztása a legelőkön, ami nem mond ellent a megfigyeléseiknek és a köztudott tudásnak. Például az utolsó előtti 202. kérdés esetén még mindig lehetséges lenne a 25-25-25-25 elosztás mellett a 25-25-25-26 elosztás is annak a testvérnek a szemszögéből, akit a király kérdez.

A helyes megfejtők között egy különdíjat is kisorsolunk, egy korábban általunk is ajánlott nagydobozos kiváló társasjátékot, a Splendor új kiadását, a Gémklub jóvoltából. A nyertes Endrey Márk lett, gratulálunk neki!

Kapcsolódó cikk a Qubiten: