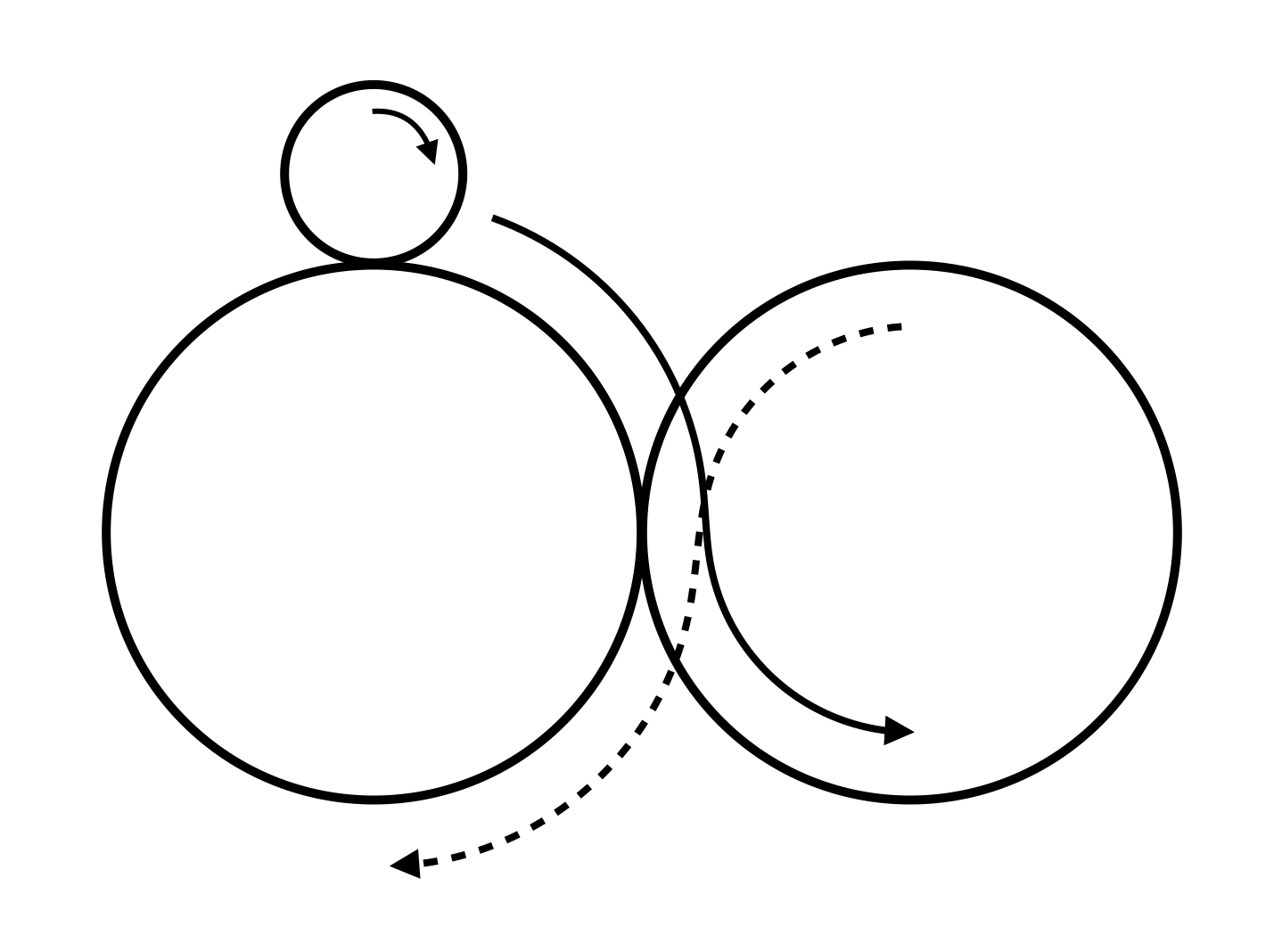
Tojásbelső című feladványunkban az volt a kérdés, hogy Kolumbusz tojásában mekkora szöggel fordul el a felső kis kör, ha azt az ábra síkjában végiggörgetjük a tojás belső falán, majd visszaérkezik a tojás csúcsához.

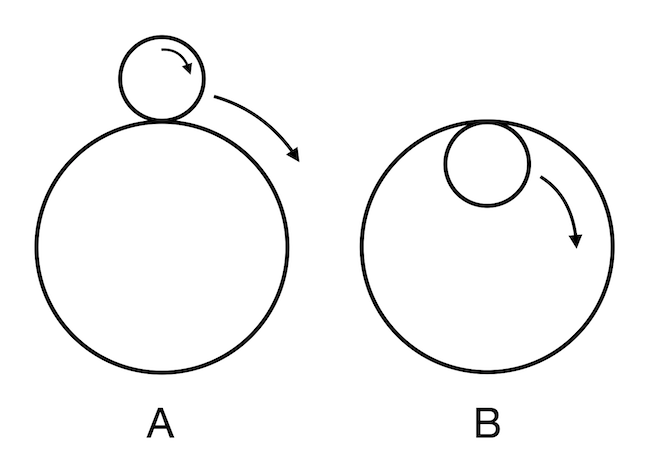
Korábban a 126. feladványunkban már volt szó körök körökön történő külső és belső görgetéséről, és a megoldásból kiderült, hogy a szögelfordulás a kerületek (vagy a sugarak) arányától függ, de egy teljes fordulatot hozzá kell adni, ha kívül gördítünk, és le kell vonni, ha belül gördítünk. Ez a jelenség a coin rotation paradox néven ismert. Ha R sugarú kör külsején gördítünk körbe egy r sugarú kört, akkor a gördített kör körbefordulásainak száma egy teljes körbegördítés után R/r+1, ha belül gördítjük, akkor R/r-1. Ha például R végtelen, az felel meg az egyenes való gördítésnek, de ebben az esetben a végtelen hosszú egyenest nem tudjuk soha megkerülni, ezért a gördítések száma is végtelen lesz. Ha R = 0, akkor az egy pontnak felel meg, ekkor a körbegördítés körbeforgásnak fog megfelelni, tehát pont egy körbegördítésre fog egy körbeforgás jutni.

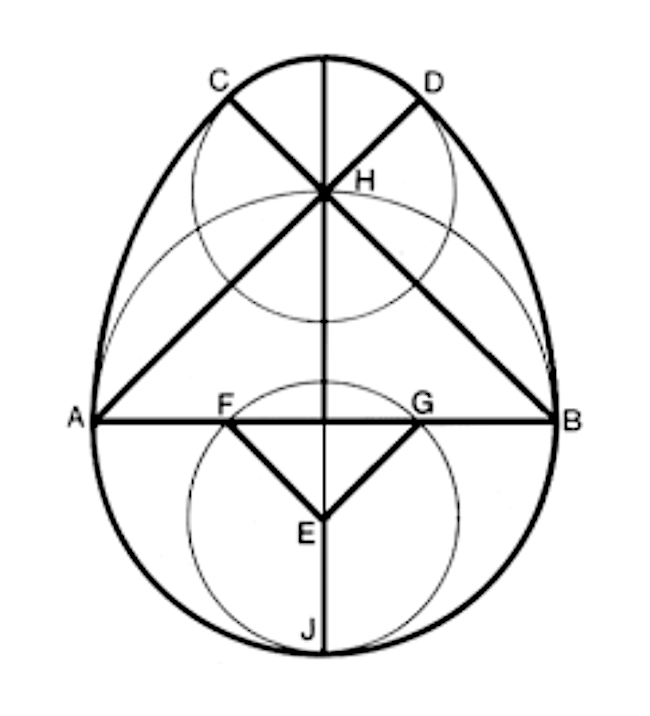
Jelen esetben használhatjuk ezeket a képleteket, csak sugár helyett a kerületeket kell beírnunk, és a tojás kerületét több körívből kell összetennünk. Ezen kívül vegyük észre – ez sok megoldónknak elkerülte a figyelmét –, hogy nem feltétlenül kell a tojás teljes kerületét figyelembe vennünk, mert a gördülés a D pontból indul, és amikor a kis kör a C ponthoz visszaér, akkor már azonnal érintkezni fog a tojás csúcsával is. Ez pedig még egy dolgot befolyásol, hogy nem 1-et, hanem csak 3/4-et kell levonnunk a belső gördítésre vonatkozó fenti képletben.

Ezek után számoljunk! Legyen az AB szakasz hossza 2. Ekkor a kis kör sugara r = 2 - √2, a kerületre pedig k = (4-2√2)·𝜋 adódik. A bejárandó út hossza két 2 sugarú nyolcadkörívből és egy 1 sugarú félkörívből tevődik össze, ami összességében s = 2·(4𝜋/8) + 1·(2𝜋/2) = 2·𝜋. Az elfordulás szöge tehát s/k - 3/4 = 1/(2 - √2) - 3/4 lesz, ami 344,56°-nak felel meg. Természetesen gondolkodhatunk úgy is, hogy ragaszkodunk az s/k-1 képlethez, és a tojás teljes kerületét vesszük figyelembe, vagyis a fenti s-hez még k/4-et hozzáadunk. Láthatjuk, hogy az eredmény ugyanaz lesz, de azért nem árt átgondolni, hogy miért működik, hiszen fordulás már nem történik azon a szakaszon.

Kapcsolódó cikk a Qubiten: