Spóroljunk a pöttyökkel!
216. feladvány: Élpöttyözött dobókocka
Lehet-e készíteni olyan dobókockát, amit a kocka csúcsain és élein pöttyözünk, de a pöttyök minden érintkező oldalhoz beszámítanak, azaz a csúcsokra rakott pöttyök három oldalhoz, az élekre rakott pöttyök pedig két oldalhoz? Egy csúcsra csak egy pöttyöt tehetünk, egy élre szintén csak egy darab nem csúcsra eső pötty kerülhet, például az él felezőpontjába. Ne feledjük továbbá, hogy a dobókockán a szemközti oldalakon lévő pöttyök számának mindig hétnek kell lennie.
A feladvány ötletét Molnár Csaba ékszerdizájner munkái inspirálták.
Tipp chevron_down
Lehet csak próbálkozni is, de ha kicsit számolunk, az segíthet. A hagyományos kockán lévő pöttyök száma 1+2+3+4+5+6 = 21. Ha viszont a egy pöttyöt egy élre rakunk, az két oldalhoz fog beszámítani, vagyis kétszeresen jelenik meg az összegben. Ebből rögtön látszódik, hogy lehetetlen olyan kockát csinálni, ahol csak az élek közepére rakunk pöttyöket, mert a 21 páratlan szám. Szükség van tehát páratlan sok csúcsra, ahova pöttyöt rakunk, ezek ugyanis háromszorosan számítanak. A hatos oldalhoz viszont legalább két csúcsra is pöttyöt kell tennünk, mert az oldalt határoló élekre rakott négy pötty nem elég. Mindezekből tehát az következik, hogy legalább három csúcsra kell pöttyöt raknunk.
Megoldás chevron_down
Egy lehetséges megoldás az alábbi.
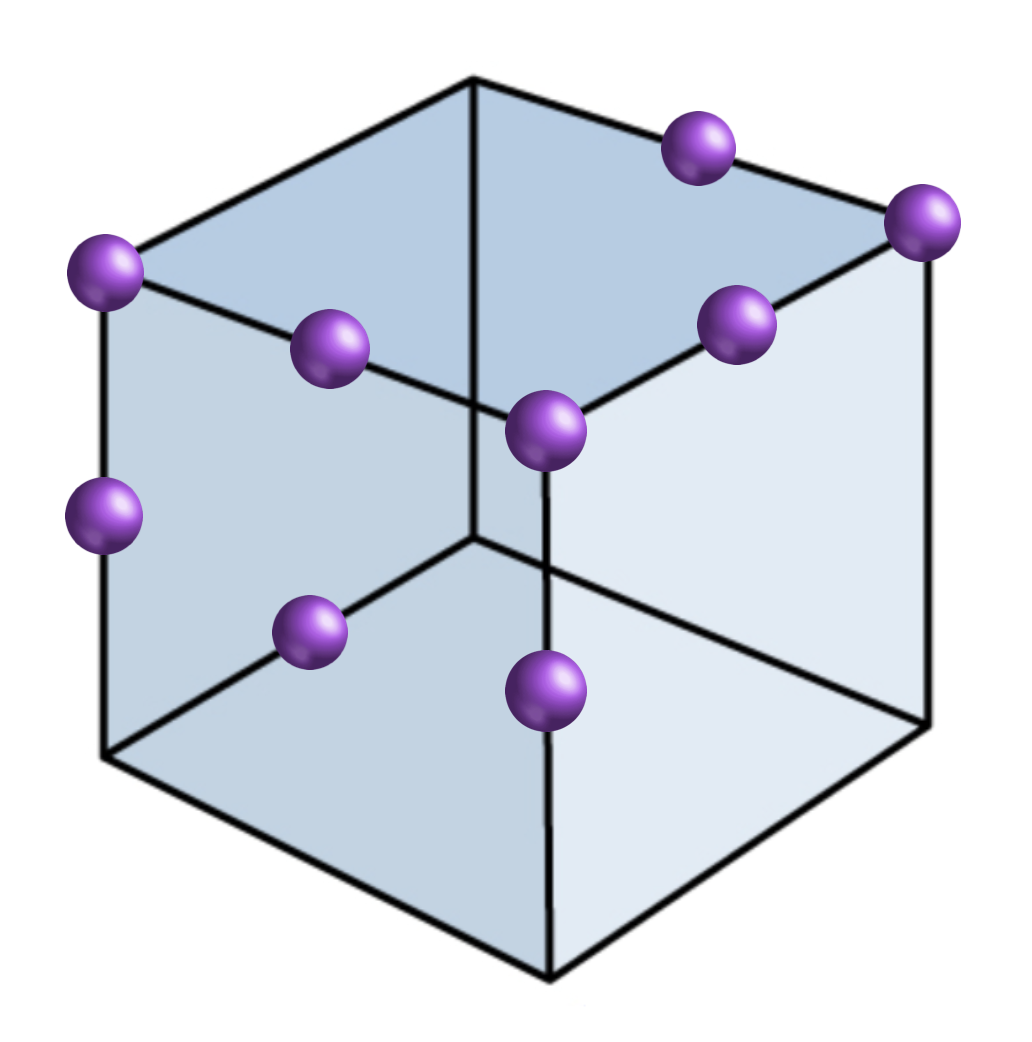
Ha tudtok más megoldást, akkor küldjétek be az eszventura@qubit.hu címre! Mi lehet a minimális pöttyszám? A legtöbb, lényegesen különböző megoldást beküldő olvasónk egy Mobee játékot nyerhet, amely korábbi, Dobble a köbön című feladványunknak egy különleges megvalósítása, amiben három különböző nehézségű készlet is található. A beküldésre egy hónap áll rendelkezésre!
Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, kognitív kutató, társasjáték-fejlesztő és bűvész.