Először is, ha azt gondolod, hogy ez nem lehetséges, akkor tévedsz. Másodszor, nincs benne olyan trükk, hogy a menedékhely odébb mászott, és hasonlók. Csak egy kis görbült geometria és logika. Továbbá koncentrálj az utolsó mondatra! Mi következik abból, hogy lassabban haladva hamarabb visszaért ugyanazon az úton haladva? Vigyázat, lehetséges, hogy tudod már, hogy hol és mire vadászott a vadász, de biztosan jól számolod a területet?

Ha ugyanazon az úton indult visszafelé, és lassabban haladva hamarabb hazaért, ebből az következik, hogy a menedékhelyig nem kellett a teljes utat megtegye visszafelé, tehát az útvonala idefelé (medve- és kesztyűvadászat közben valamikor) áthaladt a menedékhelyen. Ez persze nagyon furcsa elsőre, hiszen délre ment, majd keletre, majd vissza a legrövidebb úton a fordulóig. A keletre fordulás pontja nyilvánvalóan délebbre lévő szélességi körön van, mint a menedékhely, és keletre haladva nem változott a szélességi kör, amiből az következik, hogy a szélességi kör csakis a kesztyűért való visszaúton változhatott, vagyis a legrövidebb út vissza nem nyugatra haladt. Ez tulajdonképpen nyilvánvaló, hiszen amikor egy szélességi körön haladunk, akkor az szinte soha nem a legrövidebb út, mert a szélességi körök, nem főkörei a Föld gömbjének, ezalól egyedül az Egyenlítő a kivétel.

Világos tehát, hogy ebben a feladatban számít a földfelszín görbültsége. Amikor visszament a vadász a kesztyűért, akkor egy főkörön kellett haladjon, mert a legrövidebb úton ment, és ennek a főkörnek hosszúsági körnek kellett lennie, hiszen ha átment a menedékhelyen és elment a kesztyűig, akkor az út része volt az a déli irányú 1 kilométeres útszakasz is, amit a nap legelején tett meg, és egy tisztán déli irányú út az mindig hosszúsági kör mentén történik. Ugyanakkor északra is kellett haladjon a kesztyű felé menet, mert átment a menedékhelyen, ami északabbi szélességi körön van, tehát lényegében át kellett menjen az Északi-sarkon.

Világos tehát a szituáció: amikor kelet felé ment, akkor lényegében átment a túloldalra a kesztyű szélességi körén, de visszafelé már egy Északi-sarkon áthaladó hosszúsági körön jött. Egy tisztázandó van már csak, hogy hányszor kerülte meg eközben az Északi-sarkot: félszer, másfélszer, vagy annál is többször? Ha a kesztyű szélességi körének sugara R, akkor a keletre menő út, azaz körív hossza L = (2·k-1)·𝜋·R, ahol k tetszőleges pozitív egész szám. k = 1 felel meg annak, amikor félszer kerüli meg a vadász az Északi-sarkot, ez látszódik a bal oldali ábrán, ahol É betű jelöli az Északi-sarkot. k = 2 felel meg annak, amikor másfélszer kerüli meg a vadász az Északi-sarkot, lásd a jobb oldali ábrát.

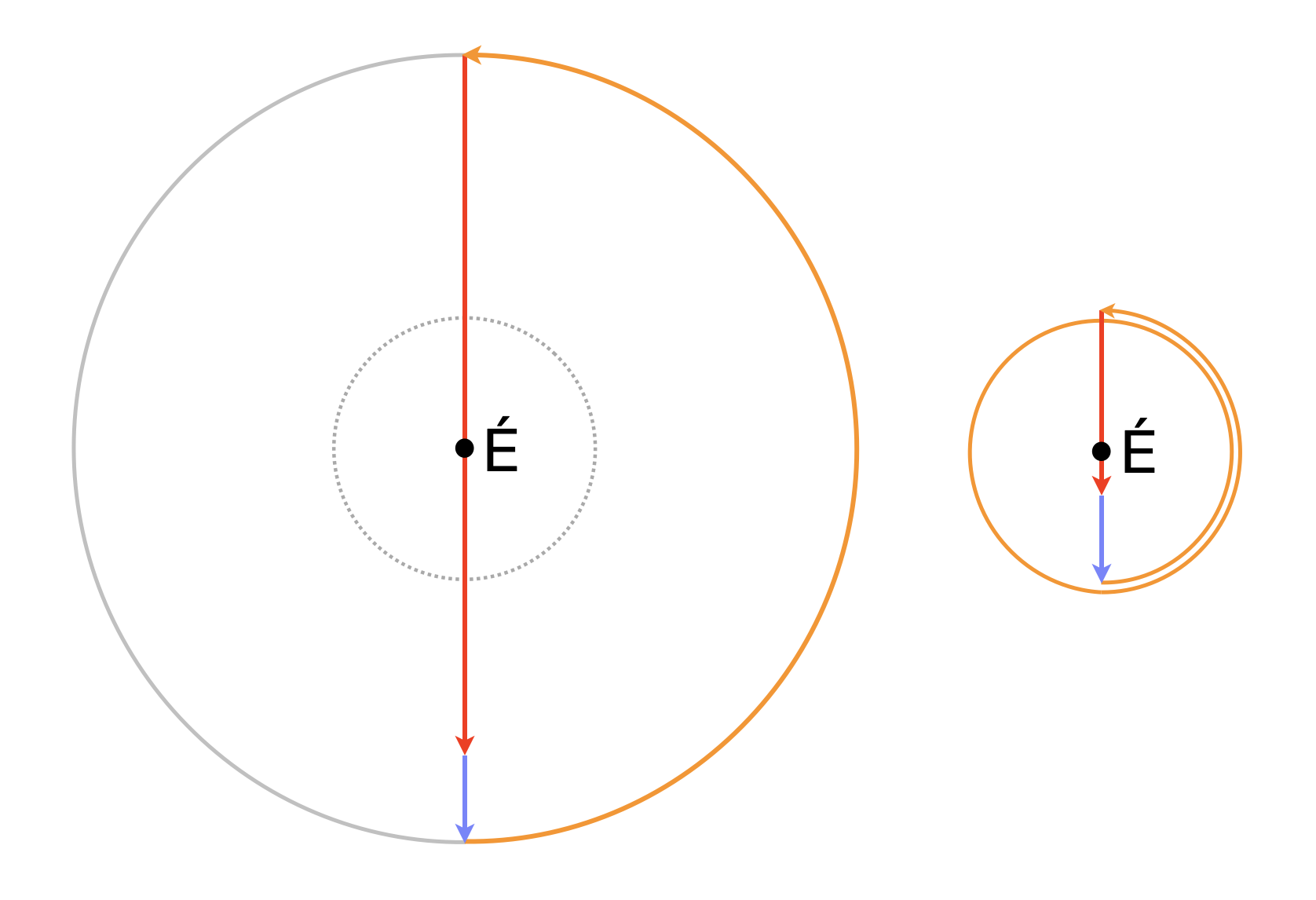
Mármost a feladat szerint L = 11 km, Ha k = 1, akkor R ≈ 3501 m adódik, ha k = 2, akkor R ≈ 1167 m adódik (harmada az előzőnek), ha pedig k ≥ 3, akkor R ≤ 700 m. Mivel viszont a feladat szerint a nap elején a vadász 1000 métert ment délre, ezért nem lehetett egy 700 méter sugarú körön belül, tehát csak az első két lehetőség marad. Ráadásul a feladat szerint mindkét lehetőség meg is valósult, mert a vadásszal ugyanaz megtörtént kétszer. A kérdés már csak az, hogy melyik nap melyik, de ez egyértelmű, hiszen dél felé költöztette át a menedékhelyét, tehát első nap volt északabbra, ami a jobb oldali ábrának felel meg, és körülbelül 4,3 négyzetkilométert nagyságú kör alakú területet járt be a vadász jegesmedvére vadászva az Északi-sark körül.