Magyar kutatók szerint a klímaváltozással a vulkáni hamufelhők is gyilkosabbakká válnak
A nagyobb vulkánkitörések, vagy ipari balesetek okozta szennyeződések nemcsak a forrás közelében szóródnak szét, veszélyeztetve a helyi környezetet, hanem a Föld távolabbi pontjaira is eljuthatnak, felhalmozódhatnak. Haszpra Tímea és Herein Mátyás, az ELTE Elméleti Fizikai Tanszékének, illetve az MTA-ELTE Elméleti Fizikai Kutatócsoportjának kutatói arra a kérdésre keresték a választ, hogy milyen szerepet játszik a terjedésben az éghajlatváltozás. A választ a Nature Scientific Reportsban publikálták március 7-én. Az ELTE közleménye szerint a magyar kutatók újszerű módon, elsőként vizsgálták a szennyeződések terjedését sokasági éghajlati modellekben, a párhuzamos klímák elméletét alkalmazva.

Kiindulásuk az az elméleti alapvetés volt, hogy az úgynevezett nagyskálájú szennyeződések terjedésének erőssége meghatározható egy, a kaotikus mechanikából már ismert mennyiséggel, a topologikus entrópia segítségével. A topologikus entrópia kapcsolatban áll a jellemzően exponenciálisan növekvő szennyeződésfelhők hosszának nyúlási ütemével.
Az ELTE közleménye szerint „a vizsgálat két különböző éghajlati modellel előállított sokasági éghajlati szimulációkat felhasználva megmutatta, hogy a klímaváltozás hatására, emelkedő globális átlaghőmérséklet mellett, közel egy évszázad alatt a szennyeződésfelhők »megnyúlási hajlandósága«, azaz nyúlási üteme globális átlagban csökken, vagyis a terjedés kevésbé hordja szét a szennyeződéseket, ezáltal bizonyos földrajzi területek nagyobb környezeti terhelésnek lehetnek kitéve, hiszen az adott területre eső koncentráció növekszik. Továbbá az is kiderült, hogy a nyúlási ütem és a relatív örvényesség között erős korreláció mutatkozik. Ez azért fontos eredmény, mert a legtöbb nagy éghajlati modell számítja a relatív örvényességet, így a fenti kapcsolatnak köszönhetően a szennyeződések nyúlási üteme közvetlen módon, terjedési modellek futtatása nélkül is megbízhatóan becsülhető”.
Korábban vulkánokkal és légkörfizikával az alábbi cikkeinkben foglalkoztunk:

Kitört Balin az Agung, leállt a légi közlekedés, de addig jó, amíg egy kis hamuval megússzuk
140 ezer embert kellett kitelepíteni a szigetről, de aggodalomra nincs ok. Ráadásul európaiként nem is kell messzire menni egy az Agungnál jóval félelmetesebb szupervulkánért.

Ritka meteorológiai jelenség alakult ki a szakadatlanul hömpölygő láva miatt Hawaiin
A füstgomolyfelhők heves, villámlással kísért, a vulkáni hamu összetétételének függvényében akár savas esőkkel kísért zivatarokat okozhatnak.
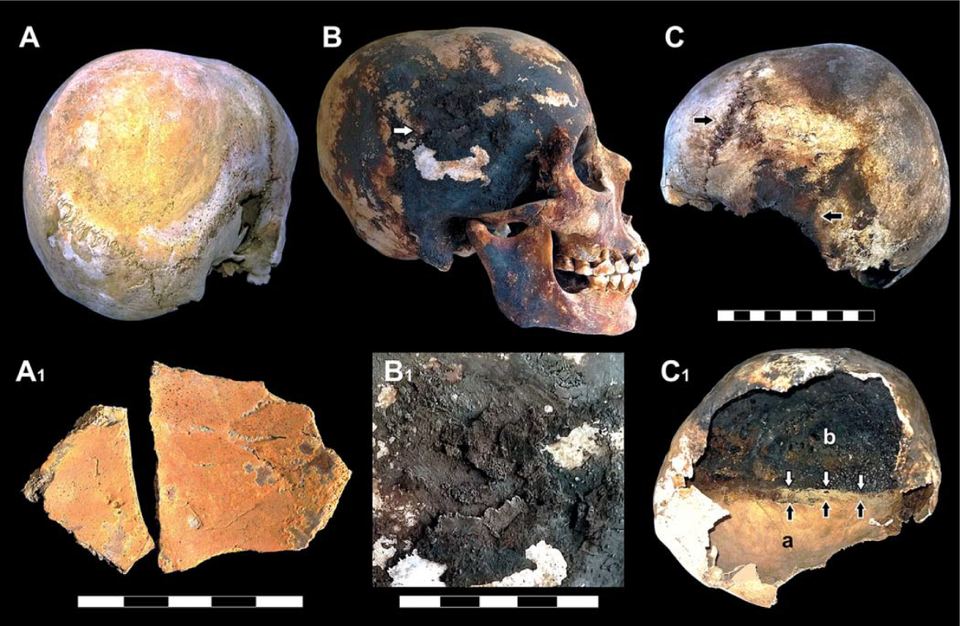
Olasz kutatók: A Vezúv áldozatainak pillanatok alatt felforrt a vérük, és szétrobbant a koponyájuk
Az i. sz. 79-es vulkánkitörés herculaneumi maradványait vizsgálta egy olasz kutatócsoport, amely alaposan megcáfolta azt a hiedelmet, hogy az áldozatok lassan égtek el.
