Korábban kitűztük a Dobble kártyajáték általánosítását, amikor nem kettő, hanem három kártyalapon kell keresni a közös szimbólumot. Ilyen típusú általánosításból idő közben egy megvásárolható játék is született, a Møbee, amiről szintén írtunk korábban.

Természetesen az általánosítás még tovább folytatható, lehet csinálni akár négy lapon egy közös szimbólumot kereső játékot is, persze az élmény egyre kevésbé lesz újszerű. Van viszont más irányú általánosításra is lehetőség, a Møbee alkotója, Ruff János matematikus a véges geometriák területét általánosító ún. blokkrendszerek felhasználásával most olyan kártyajátékot készített, amiben a Møbee gyorsasági mintázatkereső játékhoz hasonlóan szintén három lapot rakunk ki, de nem egy, hanem egyszerre két közös szimbólumot is keresünk a kártyákon.

A mai feladvány az lesz, hogy konstruáljunk egy ilyen paklit. Ehhez némi segítséget is adok. Aki viszont nem szeretne bíbelődni vele, de mihamarabb játszani szeretne egy ilyen paklival, annak ott a lehetőség, hogy támogassa a Møbee Twin játék kampányát a Brancson, a közösségi finanszírozásra kialakított magyar piactéren, és elsőként jusson hozzá egy ilyen paklihoz. Pontosabban nem is egyhez, mert sikeres kampány esetén, a játék dobozában négy pakli is lesz, számos játékmóddal és különböző nehézségi szintekkel.

Na de nézzük a segítséget. Azt elárulom, hogy a blokkrendszerek segítségével olyan játék készíthető, amiben minden kártyán ugyanannyi szimbólum szerepel, minden szimbólum ugyanannyi kártyán szerepel, de mindegyik más kártyákon. Ebből mi most az utolsó feltételen lazítani fogunk picit. De mi is az a blokkrendszer? Ezt nem kell tudni a feladvány megoldásához, de ha megnézzük az alábbi definíciót, akkor sejthetjük, hogy a blokkrendszer valami nagyon szimmetrikus dolog lehet a halmazok világában.

Legyen H egy B darab elemet tartalmazó halmaz. A H halmaz feletti Q−(B,I,T) blokkrendszer alatt H-nak olyan kitüntetett I-elemű részhalmazait (amiket blokkok-nak nevezünk) értjük, amikre teljesül, hogy bármely Q különböző elemét kiválasztva H-nak mindig éppen T darab olyan blokk lesz, amik mindegyik elemet tartalmazzák.

Ebből úgy lesz kártyajáték, hogy a H halmaz elemeit feleltetjük meg a kártyalapoknak, a blokkokat pedig az egyes szimbólumoknak, amikből mindegyik pontosan I kártyán szerepel. A definícióban Q felel meg annak, hogy hány kártyalapot csapunk fel, T pedig annak, hogy hány közös szimbólumot keresünk a felcsapott kártyákon.

Ennek megfelelően a Dobble játék 2−(B,I,1) blokkrendszeren, a Møbee játék 3−(B,I,1) blokkrendszeren, a Møbee Twin pedig 3−(B,I,2) blokkrendszeren alapul. Az előbbi két esetben, azaz T = 1 esetén végtelen sok konstrukció ismert, persze nem mindegyik praktikus kártyajátéknak, T = 2 esetében viszont, azaz az új típusú általánosítás esetén, jelenleg csak véges sok megoldás ismert.

Erről eszünkbe juthatnak a szabályos testek, amikről jól tudjuk, hogy csak véges sok létezik belőlük. Ennek egyik oka nyilván az, ha elkezdünk egy testet felépíteni szabályos lapokból, akkor nem biztos, hogy körbezáródik a test. Ahhoz, hogy körbezáródjon, bizonyos feltételeknek meg kell feleljen, ahogy a blokkrendszerek esetében is a paraméterek között bizonyos összefüggéseknek teljesülniük kell, hogy egyáltalán esély legyen találni olyan blokkrendszert, azaz nem minden Q, B, I, T kombináció lehetséges.

Éppen ezért az alábbi feladványban meg fogom adni egy konkrét keresett kártyapakli paramétereit segítségként. A pakli, amit keresni fogunk azonban nem igazi blokkrendszer lesz, egy picit lazítunk a feltételeken. A blokkrendszerek esetében követelmény, hogy minden blokk H-nak különböző részhalmaza legyen, ha azonban megengedjük azt, hogy kétszer is szerepeljen ugyanaz a blokk, az azt jelenti a játék nyelvén, hogy megengedjük, hogy ugyanazokra a kártyákra akár kétszer is rajzoljunk szimbólumot, vagyis legyen két olyan szimbólum, amik mindig együtt fordulnak elő, mint a jin és a jang.

250. feladvány: Møbee általánosítás

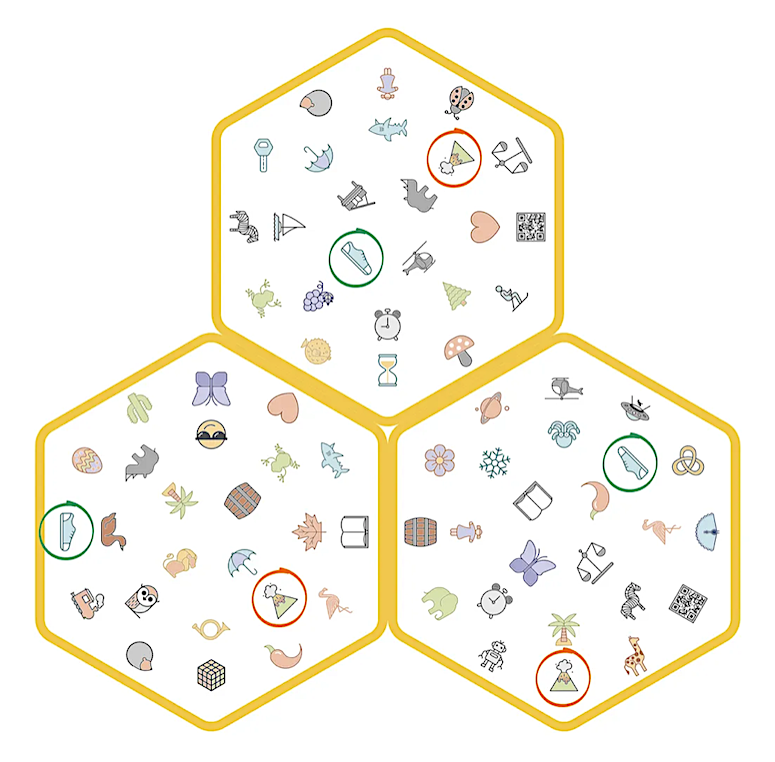
A Møbee kártyajátékban bármely három kártyalap esetén találunk pontosan egy szimbólumot, amelyik mindhárom lapon rajta van. Most olyan általánosítást keresünk, hogy bármely három kártyalap esetén legyen pontosan két közös szimbólum, ahogy a legelső ábrán is látható.

Amikor a Dobble három lapra történő legegyszerűbb általánosítását néztük egy korábbi cikkünkben, annak is köze volt a kockához, az ún. kockatérhez. Most is lesz egy olyan nyolc lapos konstrukció, amit a kocka csúcsaihoz lehet kötni. Azt is elárulom, hogy a keresett pakliban 28 szimbólum szerepel, és minden szimbólum pontosan négy kártyán van rajta. Ezen kívül legyen a pakliban két szimbólum pár (jin és jang, továbbá a mágneses északi és déli pólus), amik páronként mindig együtt szerepelnek, az összes többi szimbólum viszont olyan négy lapon szerepeljen, hogy semelyik másik szimbólum ne szerepeljen pont azon a négy lapon.

A fenti feltételek mellett adjuk meg, hogyan kéne a szóban forgó paklit elkészíteni.

Megoldás

Először nézzük a kockán hány kitérő élpár van úgy, hogy az élek végpontjai mind különböznek. Könnyen belátható, ha kiválasztunk egy élt a kockán, akkor a végpontjaiból kiinduló éleken és a vele párhuzamos éleken kívül négy él marad, amit választani lehet hozzá. Mivel pedig tizenkét éle van a kockának ez összesen 12 × 4 = 48 lehetőség lenne, de mindegyiket kétszer számoltuk meg, tehát a valódi lehetőségek száma 24.

A kocka csúcsai reprezentálják a lapokat a kártyapakliban. Minden szimbólumhoz feleltessünk meg egy kitérő élpárt, azaz azokra a kártyalapokra kerüljön fel a szimbólum, aminek csúcsait az élpár lefedi. Ezzel van már 24 szimbólumunk, de kéne még négy. A hiányzó négy legyen a feladatban megadott szimbólum pár, amiket a kocka csúcsai által kifeszített két szabályos tetraéder csúcsaihoz rendeljünk, lásd a jobb oldali kockát alább, ahol a három fekete és egy kék pont kijelöl egy tetraédert, és a maradék csúcsok kijelölik a másikat. Az egyik tetraéder csúcsaihoz tartozó lapokra tegyük fel például a jin és jang szimbólumokat, a másik tetraéder csúcsaihoz tartozó lapokra pedig az északi és déli mágneses pólusokat.

Most nézzük meg, hogy az így konstruált pakli megfelelő-e. Nézzük hányféleképpen választhatunk három lapot, azaz kocka csúcsokat. Tekintettel arra, hogy az egész konstrukciót a kockához, mint szabályos testhez kötöttük, könnyen belátható, hogy a forgásszimmetria miatt elegendő csak az alábbi három eset ellenőrizni, ahol a fekete pöttyök jelölik a kiválasztott csúcsokat.

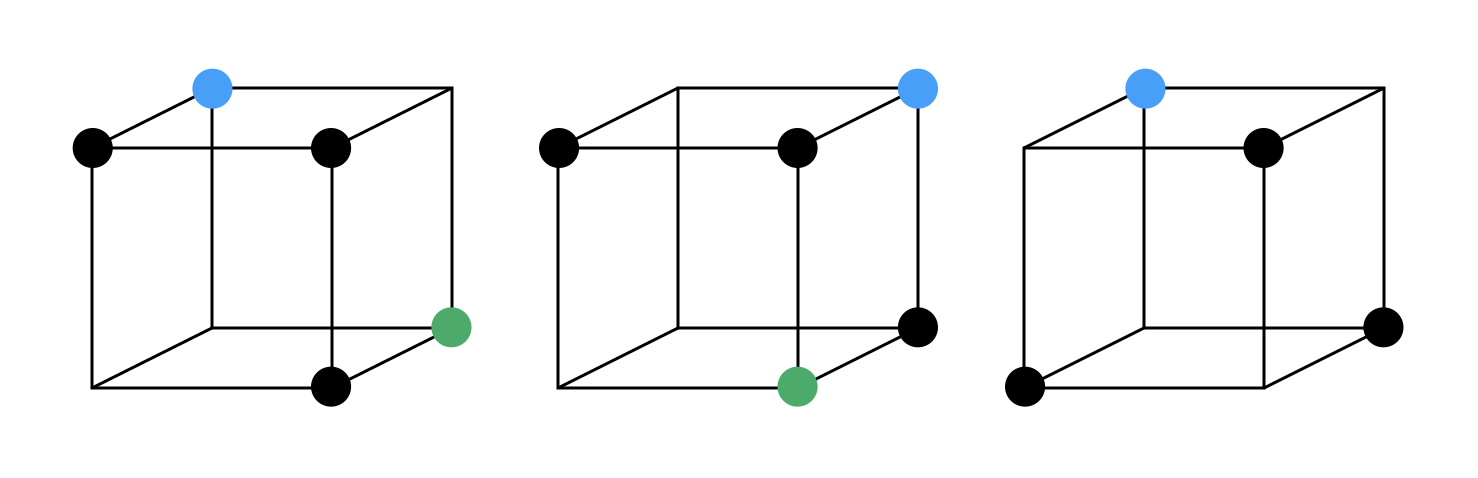
Mármost nyilvánvaló, hogyha a három csúcsot, azaz kártyát, a bal oldali minta szerint választottuk, akkor pontosan kétféle módon lehet kitérő élpárrá bővíteni egy csúcs hozzáadásával, tetraéderré pedig nem lehet, tehát pontosan két közös szimbólum lesz a három lapon, nevezetesen azokhoz a kitérő élpárokhoz tartozó szimbólumok, amikké bővíteni tudjuk a kék vagy a zöld csúcs hozzávételével.

Hasonlóan, a középső esetben is kétféle módon lehet kitérő élpárrá bővíteni (lásd az ott lévő kék és zöld pontokat) egy csúcs hozzáadásával, tetraéderré pedig nem lehet. Végül a jobb oldali esetben nem lehet élpárrá bővíteni, viszont tetraéderré igen. És bár csak egy tetraéderré lehet, a kék pont hozzávételével, de ahhoz duplán tartozik szimbólum, ezért egy megfelelő paklit kaptunk.

Ti tudtok más megoldást is?

Ha szereted a fejtörőket, tekintsd meg korábbi feladványainkat is! Ha megjegyzésed lenne, vagy feladványt javasolnál, írj az eszventura@qubit.hu e-mail címre! Ha pedig tetszik a rovat, akkor ezt a Vendégkönyvben kifejezésre juttathatod.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, kognitív kutató, társasjáték-fejlesztő és bűvész.