Előző héten kimaradt az Ész Ventura, ezért most bepótoljuk, és két feladvány is lesz. Ezekhez a feladványokhoz nem kell más csak egy füles bögre, és egy filc. Lehetőleg olyan bögrét válasszunk, ami világos színű és nincs rajta semmilyen írás vagy ábra, filcből pedig olyant, amit le tudunk törölni, ha azzal a bögrére rajzolunk.

Ezek olyan eszközök, amik minden háztartásban fellelhetők. Ha elég kreatív vagy, és ki tudsz találni te is egy logikai feladványt valamilyen jellegzetes hétköznapi tárggyal, amely minden háztartásban vagy a ház körül megtalálható, akkor

ne habozz, indulj a második Zagyvai András játéktervező versenyen! A verseny tavaly került kitűzésre, de a beadási határidőt meghosszabbítottuk egy évvel, így idén október 15-ig lehet beküldeni játékokat. A Reflexshop és Typotex Kiadó támogatásával megrendezett verseny díjainak átadására a 18. Országos Ördöglakat Találkozón fog sor kerülni 2025. november 15-én a Magyar Kereskedelmi és Vendéglátóipari Múzeumban, ahol a nyertes játékok egyúttal kiállításra is kerülnek. A versenyen való indulás ingyenes, a további részleteket lásd korábbi cikkünkben

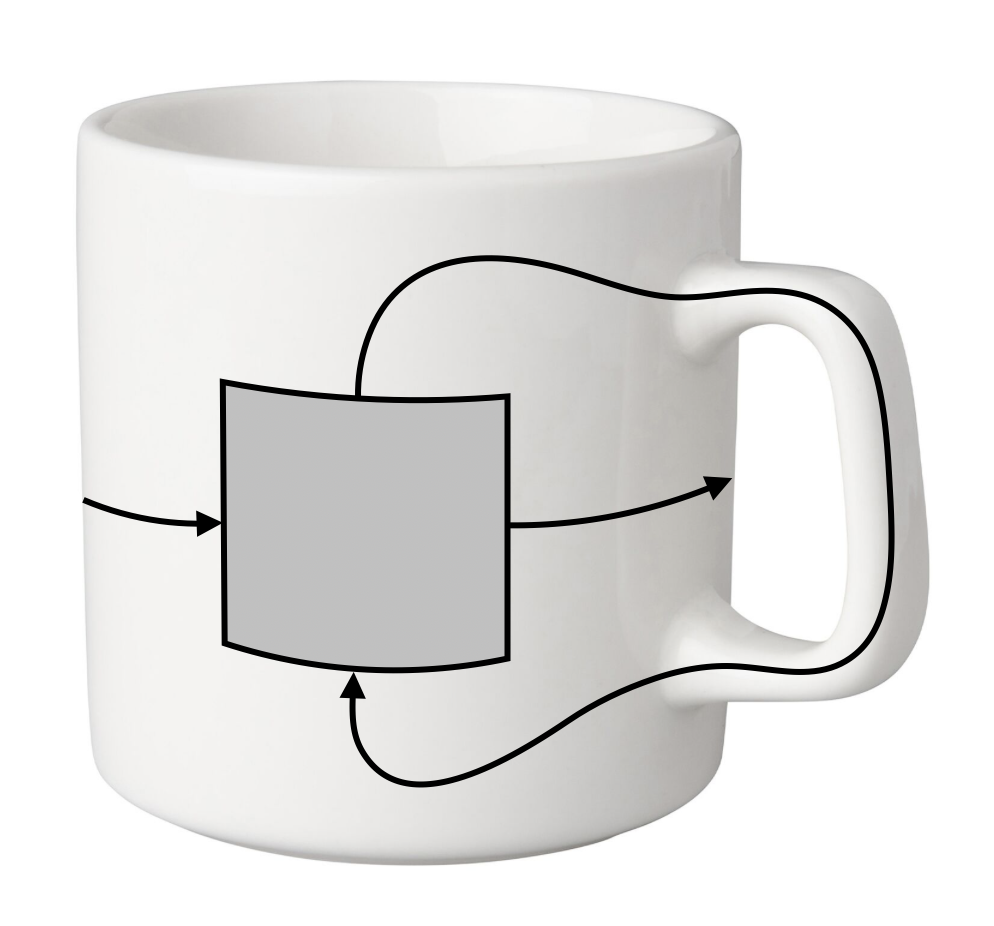
No de térjünk vissza az e heti feladványokra. A feladat az lesz, hogy adott számú pöttyöt és azokat megfelelő módon összekötő vonalakat rajzoljunk egy pontosan egy füllel rendelkező bögrére úgy, hogy a vonalak ne haladjanak át egymáson. Lényegében tehát az élek metszése nélkül bögrére rajzolható gráfokat keresünk, szakszóval tóruszra rajzolható gráfokat. A topológusok számára (matematikusok egy különleges fajtája, akikről korábban itt írtunk) ugyanis, egy füles bögre, és egy tórusz ugyanaz, mert átdeformálhatók egymásba, ahogy az alábbi ábrán is látható. Ha tehát egy gráfot rá tudunk rajzolni az egyikre az élek metszése nélkül, akkor az ábra a felülettel együtt átdeformálható, tehát a másikra is lerajzolható metszés nélkül.

Jól ismert például, hogy a síkba a teljes öt pontú gráf se lerajzolható az összekötő vonalak metszése nélkül, míg a tóruszra egy teljes hét pontú gráf is lerajzolható. Teljes gráf alatt azt értjük, hogy minden pont minden másikkal össze van kötve, azaz a hét pontú gráf esetén minden pont hat másik ponttal. Ezt tóruszra rajzolva könnyű megtenni, mert a tórusz öve mentén felvéve a hét pontot, minden pontot összeköthetünk a szomszédaival az „egyenlítő” mentén, a jobbra lévő másod és harmad szomszédaival pedig felfele indulva és jobbra csavarodva, a balra lévő másod és harmad szomszédaival pedig lefele indulva és balra csavarodva, lásd az ábrát és a videót.

De vajon lehet-e még több pontot a tóruszra rajzolni úgy, hogy minden pont hat másikkal össze van kötve? Erről szól az alábbi két feladat, ahol ugyanezt nyolc és kilenc ponttal szeretnénk megcsinálni. Elsőre talán úgy tűnhet, hogy ha kilenc pontra megoldjuk a feladatot, akkor abból elhagyva egy pontot, a nyolc pontosra is kapunk egy megoldást, de ez nem feltétlenül van így. Gondoljátok át, miért nem?

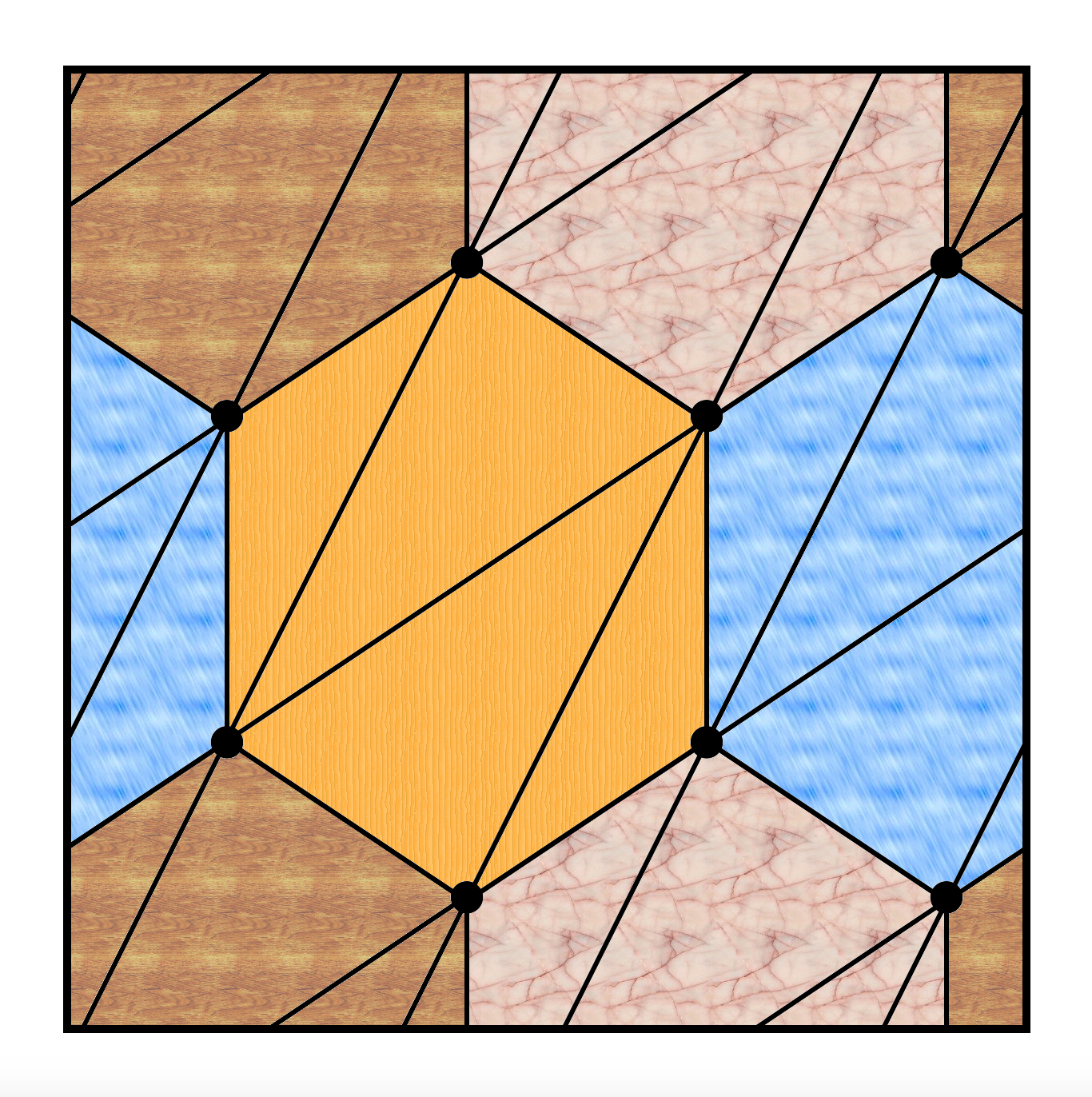
251. feladvány: Nyolc pontú sűrű gráf bögrére

Rajzolj 8 pöttyöt egy füles bögrére, és kösd össze őket egymást nem metsző vonalakkal úgy, hogy minden pötty hat másikkal legyen összekötve!

1. Tipp

A jó hír az, hogy nem kell térben gondolkodni! Mint ahogyan azt már említettük, a bögre átdeformálható tórusszá, a tórusz pedig reprezentálható egy négyzettel, csak annyit kell tenni, hogy amikor a négyzet egyik oldalán kimegyünk, akkor a szemközti oldalon ugyanott bejövünk, ahogy például a Snake számítógépes vagy telefonon játék képernyőjén is szokás. Ez azért van, mert egy négyzet szemközti oldalait összeragasztva ugye hengert kapunk, egy henger két végét összeragsztva pedig tóruszt.

A végén a bögrére könnyű visszarajzolni a négyzeten talált megoldásunkat, mert az egyik irányba kimenő vonalakat el tudjuk vinni a fül alatt körbe a bögrén metszés nélkül, a másik irányba kimenő vonalakat pedig át tudjuk vinni a fülön keresztül, ami lényegében hídként funkcionál, és a fül alatti „forgalmat” kikerüli, azaz áthidalja.

Megoldás

Egy lehetséges megoldás, ha egy hatszögrácsban gondolkodunk. Hatszögből négy darab (lásd a különböző színeket) fér fel a tóruszra úgy, hogy összesen nyolc pontunk legyen, és ha továbbra is szem előtt tartunk valamiféle szimmetriát, akkor néhány átlót behúzva a hatszögekbe az alábbi megoldást kaphatjuk.

252. feladvány: Kilenc pontú sűrű gráf bögrére

Rajzolj 9 pöttyöt egy füles bögrére, és kösd össze őket egymást nem metsző vonalakkal úgy, hogy minden pötty hat másikkal legyen összekötve!

Megoldás

Most négyzetrácsban érdemes gondolkodni, és az átlókat azonos irányba behúzva minden kis négyzetbe éppen a feladat feltételeit teljesítő megoldást kapunk.

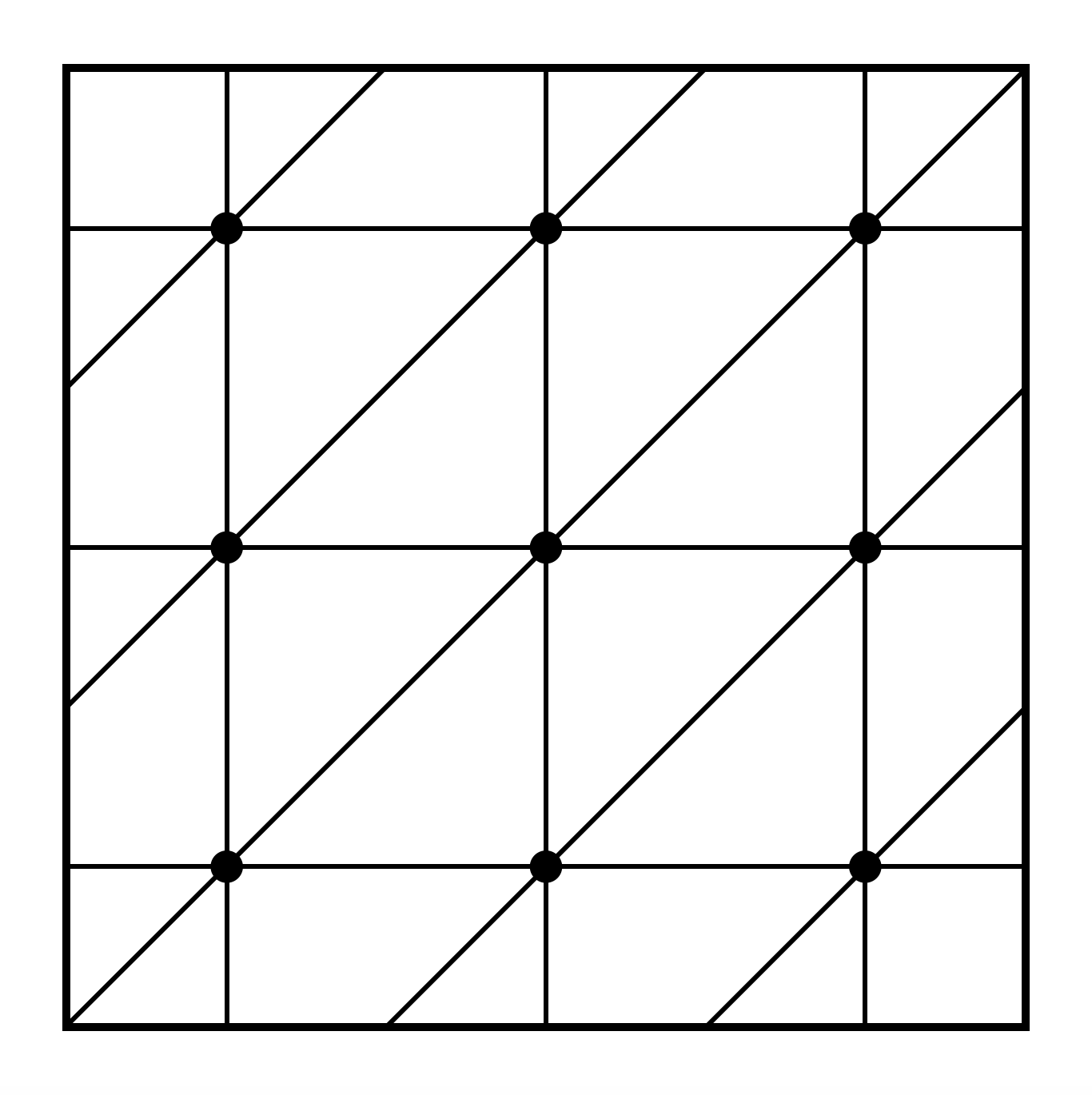
Megjegyzés: Ebből a rajzból kihagyva mondjuk a középső pontot és a belőle menő éleket, nem kapunk egy nyolc pontos megoldást, mert a középsővel szomszédos hat pöttynek elveszik egy-egy éle. Ahhoz hogy ezt kijavítsuk, be kéne húznunk három plusz élt a hat pontból képzett pontpárok közé, de úgy, hogy új összeköttetések keletkezzenek és ne is messék egymást a élek, és ez sajnos nem lehetséges. Ellenőrizzétek le!

Ha szereted a fejtörőket, tekintsd meg korábbi feladványainkat is! Ha megjegyzésed lenne, vagy feladványt javasolnál, írj az eszventura@qubit.hu e-mail címre! Ha pedig tetszik a rovat, akkor ezt a Vendégkönyvben kifejezésre juttathatod.

Az Ész Ventura feladványügyi rovat gazdája: Gáspár Merse Előd fizikus, kognitív kutató, társasjáték-fejlesztő és bűvész.