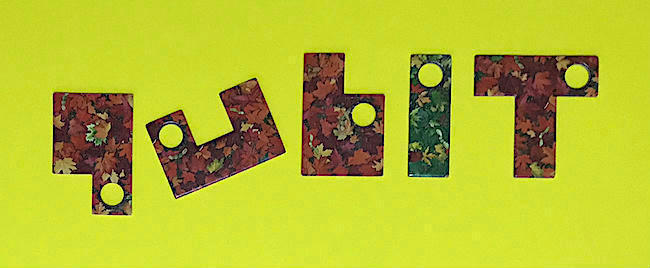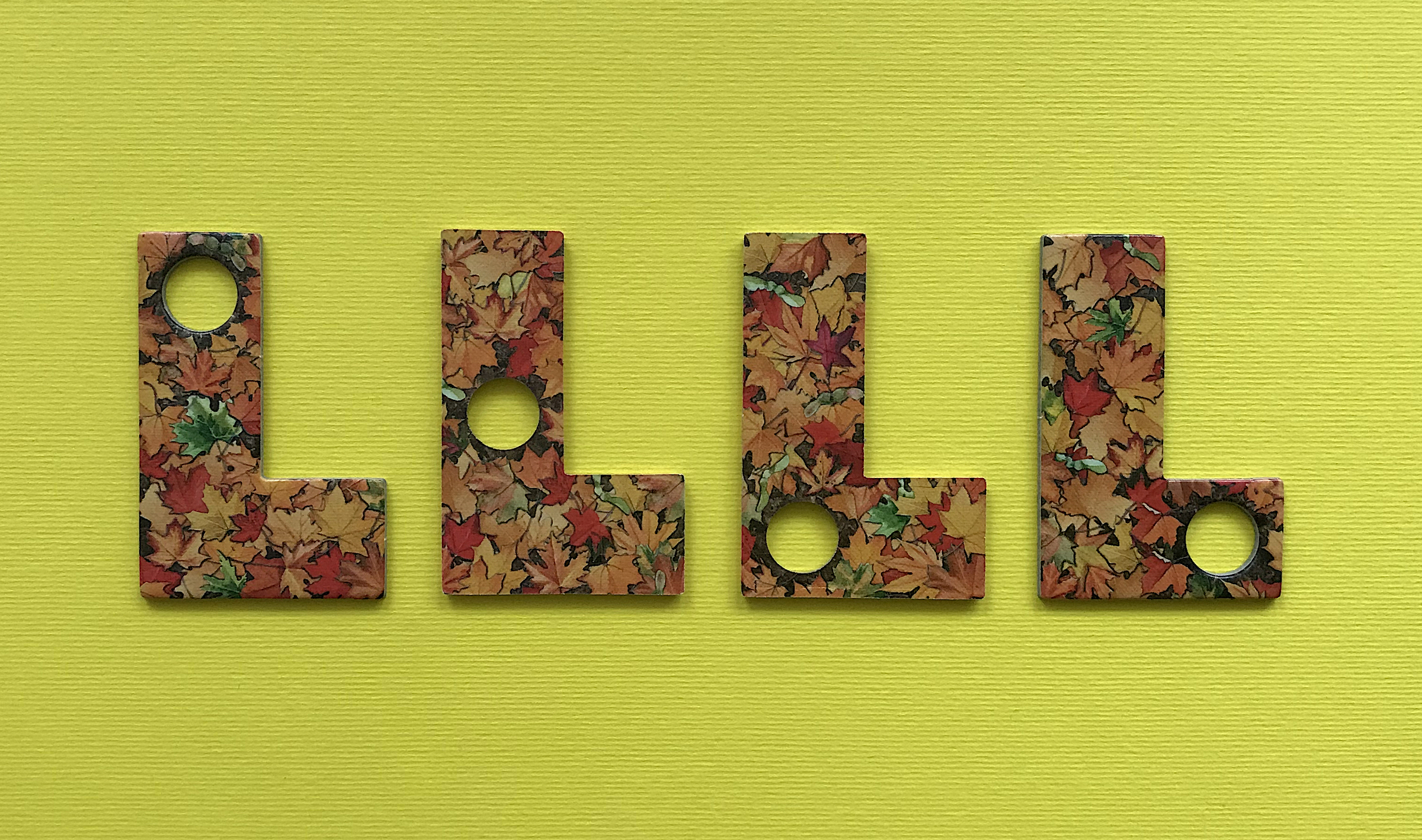Az egymás után következő 79., 80. és 81. feladványunkban lyukas poliominó elemekkel tűztünk ki kirakós feladatokat. Ilyen elemek találhatók Uwe Rosenberg Indián nyár nevű társasjátékában, melyről társasjátékos rovatunkban is írtunk már. Aki a három feladvány valamelyikére helyes megoldást küldött, a megoldások közlése után részt fog venni egy nyereménysorsoláson, amin a ComPaYa jóvoltából egy példányt sorsolunk ki ebből a nagy dobozos különleges játékból. Figyelem, van még esély bekerülni a sorsolásba, lásd a cikk végét! Most pedig következzen az első ilyen feladvány megoldása.

A feladat az volt, hogy a qubit fent látható lyukas betűinek mindegyikét felhasználva rakjunk ki egy olyan alakzatot síkban, ami valamilyen szimmetriával rendelkezik, lyukakkal együtt. A szimmetria lehet például tengelyes tükrözés, vagy akár forgatás is. Az elemeket meg lehet fordítani, de az elemek nem fedhetik át egymást. Egy lehetséges megoldás alább látható.

Ha valaki szeretne bekerülni a sorsolásba, akkor a másik két feladat megoldásának megjelenéséig van még ideje beküldeni megoldást a következő bónusz kérdések valamelyikére. Van-e más megoldás? Vagy be tudod bizonyítani, hogy nincsen? Van-e más megoldás akkor, ha ha nem követeljük meg, hogy a lyukak mintázata is ugyanazt a szimmetriát mutassa? Tehát külön-külön szeretnénk, hogy az elemek lyukak nélkül alkossanak egy szimmetrikus alakzatot, a lyukak mintázata pedig mutathat egy másfajta szimmetriát. És abban az esetben, ha lecseréljük az u betűt az alábbi ábrán szereplőre, amiben a lyuk máshol van, akkor van megoldás? Van-e ezekre az elemekre olyan megoldás, ahol az alakzat körvonala illetve a lyukak külön-külön követnek akár egymástól eltérő szimmetriát?