Mikor és mennyi időre érdemes bevezetni a kijárási tilalmat Magyarországon?

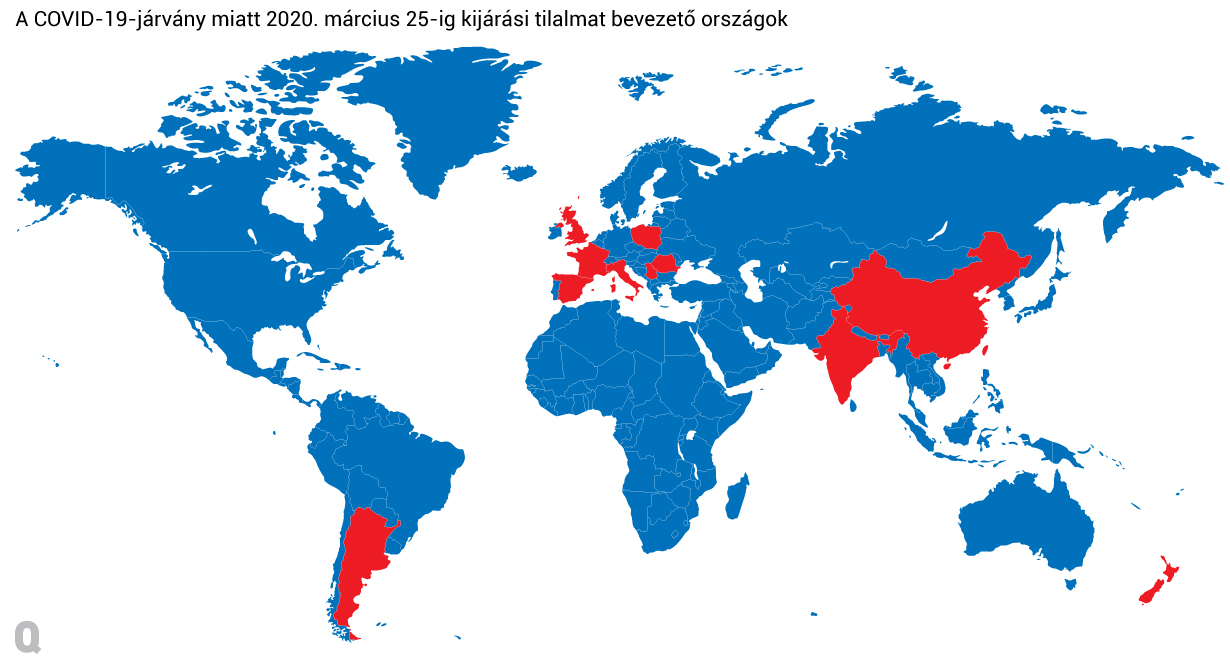
Mostanra a világ több országában rendeltek el különböző mértékű kijárási tilalmat, így Indiában, Kínában és Új-Zélandon, az európai országok közül többek között Franciaországban, Lengyelországban, Nagy-Britanniában, Olaszországban és Spanyolországban. Máshol, így Magyarországon is, sokan azt találgatják, mikor fogják bevezetni, esetleg nem értik, hogy eddig miért nem vezettek még be a lakhelyelhagyást korlátozó intézkedéseket. Ennek a cikknek a témája az alábbi kérdés lesz.
Mikor és mennyi időre érdemes kijárási tilalmat bevezetni?
Ha a járvány az egész országban elterjedt, ahogy nálunk, akkor egy néhány hetes általános kijárási tilalom valószínűleg már nem tudja megállítani a vírust, csak eltolni és enyhíteni a tetőzést. Ha túl korán vezetjük be, akkor talán fölösleges gazdasági károkat szenvedünk, ha viszont az előre várható tetőzéshez képest túl későn, akkor nem tudja időben kifejteni a hatását. Ha nem szeretnénk nagyon hosszú ideig nagyon szigorú kijárási tilalmat, akkor pontosan kellene tudni, hogy mikor érdemes bevezetni, milyen, szigorral és mennyi időre. Ebben segítenek a járványdinamikai modellek.
Az alábbiakban a korábban már ismertetett és a többek által használt SEIR járványterjedési modell segítségével járjuk körbe a fenti kérdést. Nézzük meg, mikorra kell időzítenünk a karantént ahhoz, hogy a lehető leghatékonyabb legyen, ha mondjuk két vagy három hétre szeretnénk bevezetni. A hatékonyságot abban mérjük, hogy mennyire tudjuk leszorítani a fertőzöttek számát a tetőzés idején, vagyis mennyire tudjuk csökkenteni az egyszerre fertőzésben lévők számának maximumát, ezzel legalább részben tehermentesítve a kórházi ellátórendszert.
A karantént a SEIR modellben úgy modellezzük, hogy a karantén időtartamára megváltoztatjuk a β paraméter értékét, ami azzal arányos, hogy egy fertőzött átlagosan hány másik embernek adja tovább a fertőzést. Ezt mondjuk a felére csökkentjük, de feltesszük, hogy a kijárási tilalom feloldása után a ráta értéke visszaáll a tilalom előtti értékre.
Az alábbiakban látható, hogy mikorra kell időzíteni egy ilyen kéthetes kijárási tilalmat ahhoz, hogy a lehető legjobb hatást fejtse ki. Az előző cikkbeli becsült paraméterekkel számolva (R0=2,6 és 5000 fertőzött) azt kapjuk, hogy a kijárási tilalmat (halványpiros sáv) 33 nap múlva, azaz a járvány tilalom nélkül várható tetőzése előtt pontosan két héttel kell bevezetni.
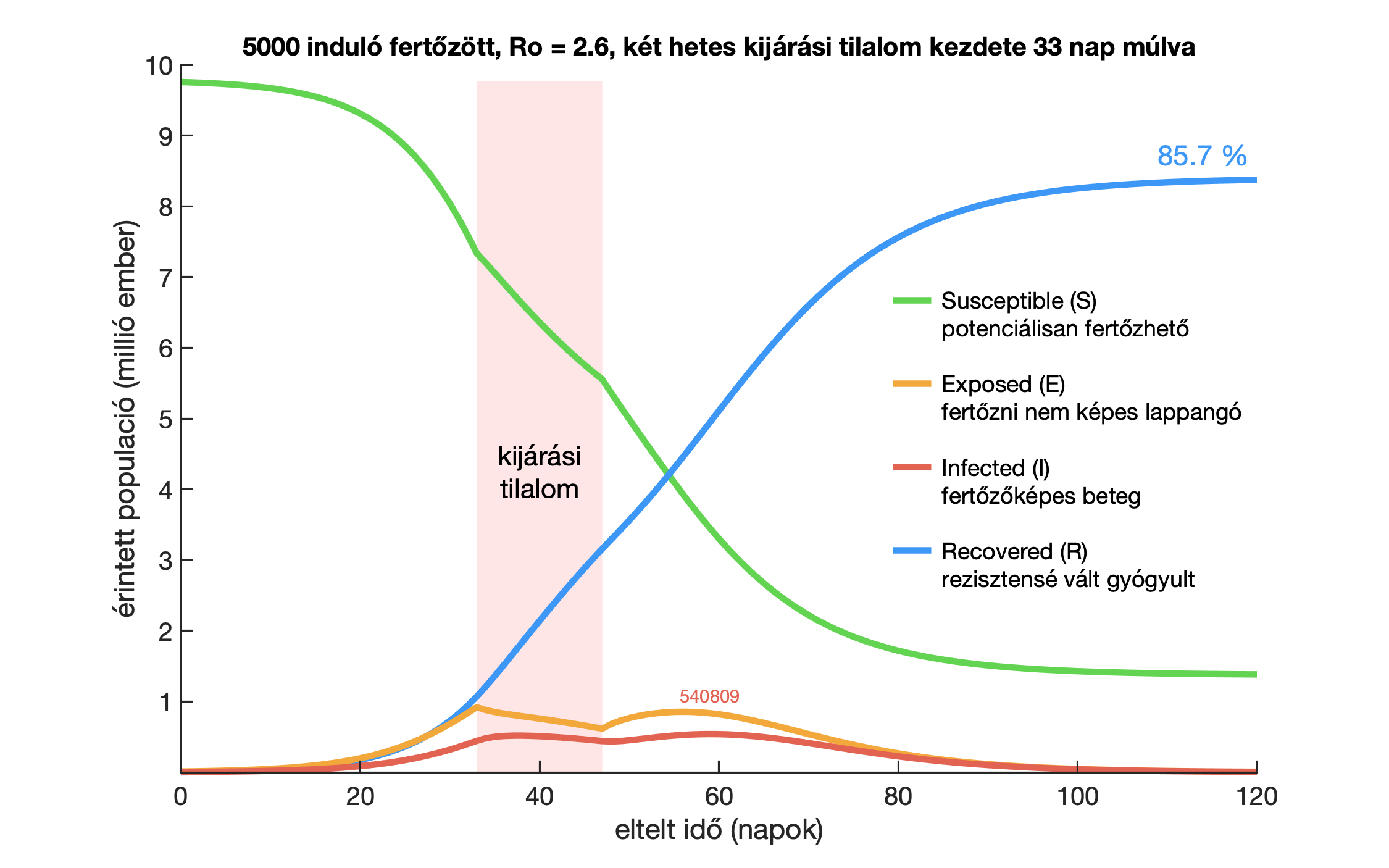
Ahogy azt a korábbi cikkünkben már kifejtettük, a fertőzöttek számának nem ismerete az egész görbét eltolhatja, a kijárási tilalom bevezetésének ideje azonban a tetőzéshez viszonyítva lényegében nem változik. Tehát nem a 33 nap a lényeg, mert azt félrebecsülheti a modell, hanem az, hogy az optimálisan időzített kijárási tilalom vége a fenti esetben épp a tilalom nélküli tetőpontra esik, vagyis azt a tetőzés előtt két héttel kell elkezdeni.
Azt is láthatjuk, hogy a kijárási tilalom bevezetése le tudja vágni és ki tudja lapítani a piros járványgörbe csúcsát, és a tetőzésnél majdnem egymilliós fertőzött-szám helyett (lásd korábbi cikkünket) a fenti példában ezt letornáztuk félmillióra, ezt a terhelést viszont negyven napig kell bírni. Megjegyezzük, hogy kéthetes tilalom helyett egy háromhetes kijárási tilalom szinte azonos eredményekre vezet – abban az esetben a modell szerint 31 nap múlva kellene bevezetni a korlátozást, és kb. 50 napig 450 ezer lenne a fertőzöttek száma.
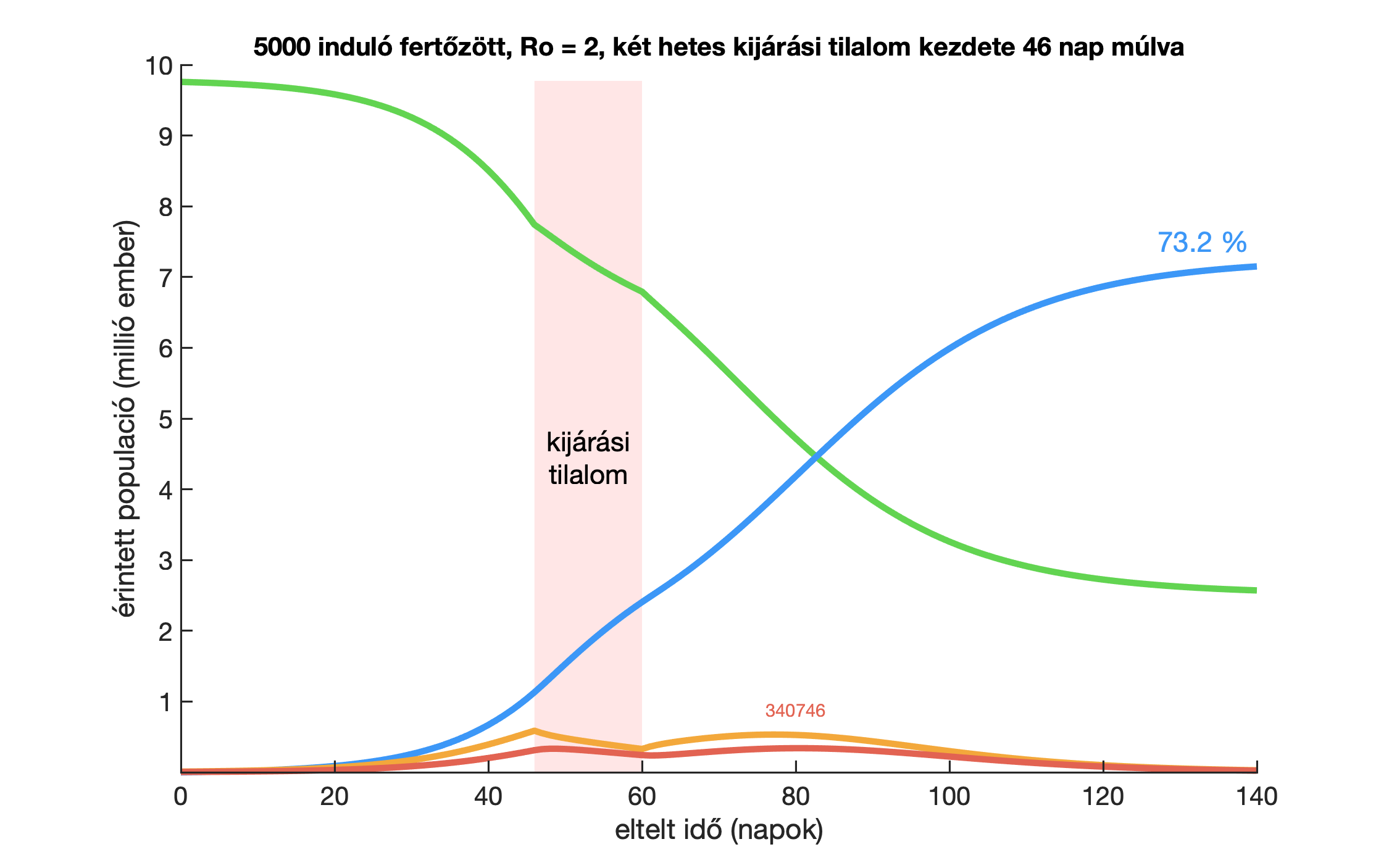
Nézzük meg még ezt az ábrát abban az esetben, ha egy kicsit derűlátóbbak vagyunk, és azt feltételezzük, hogy a fertőzés alap szaporodási rátája, vagyis az R0=2 már most, és ezt szorítjuk le felére. Ebben az esetben a modell szerint a fertőzöttek számát a tetőzés idejére le lehetne tornázni 340 ezerig, és a populációnak csak 73 százaléka esne át a betegségen.
Mint azt fent említettük, sokkal hosszabb kijárási tilalom bevezetésének nincs arányosan jelentősebb hatása. De azért nézzük meg, mikorra lenne érdemes időzíteni különböző hosszúságú tilalmakat, és mekkora lenne a hatásuk. Az alábbi ábrán azt láthatjuk, hogy 1, 2, 3 vagy 4 hetes kijárási tilalom esetén mekkora lenne az egyszerre fertőzöttek maximális száma, annak függvényében, hogy mikor vezetik be a kijárási tilalmat. Nyilvánvaló, hogy az optimális kezdési időpont a görbék legalacsonyabb pontjához tartozik, azaz 2, 3 vagy 4 hetes tilalom esetén rendre 33, 31 vagy 29 nap múlva. Ebben tehát nincs nagy eltérés.
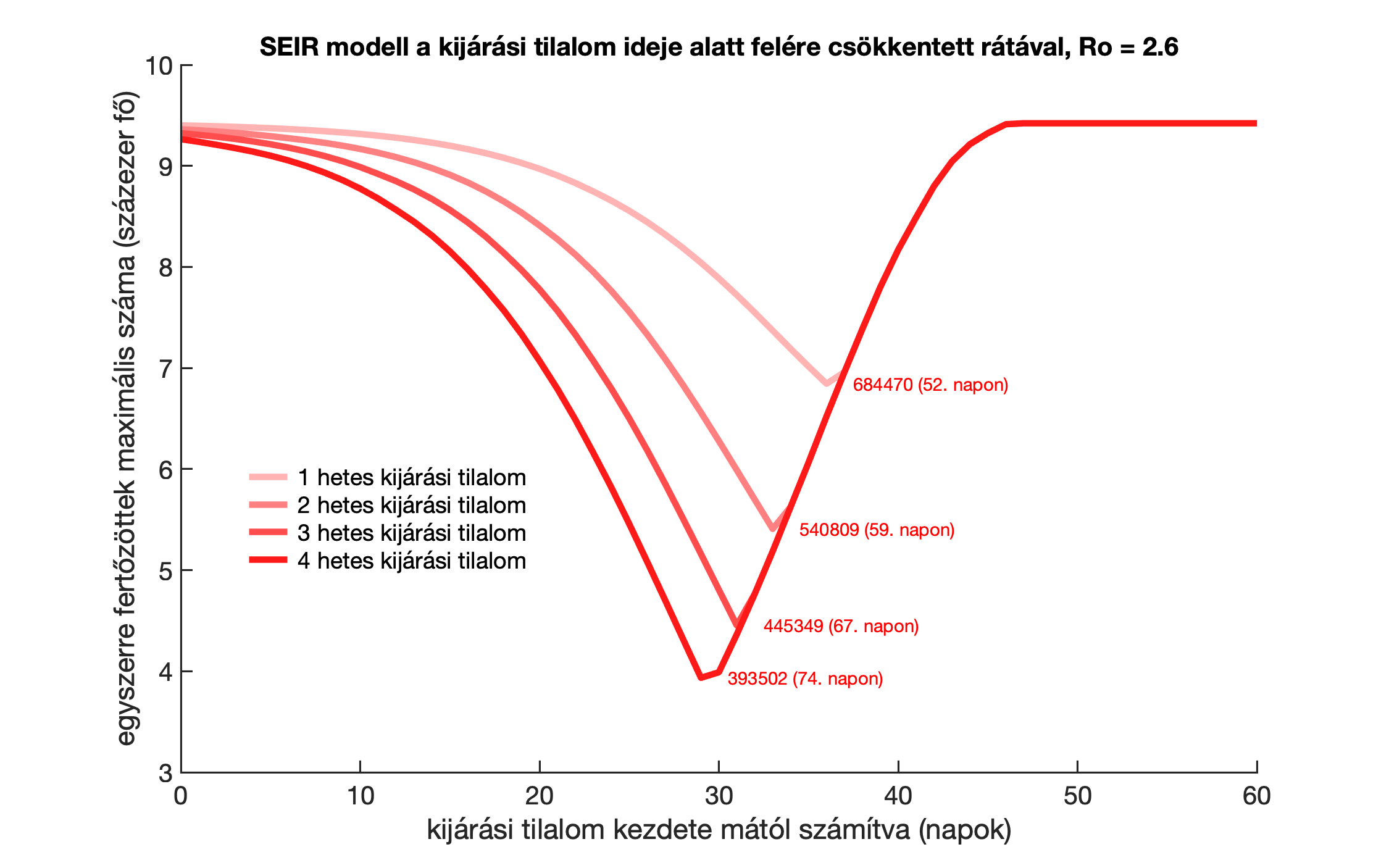
Az ábrán az optimális völgypontok mellé az is oda van írva, hogy mennyire tudja leszorítani a helyes időben bevezetett kijárási tilalom az egyszerre fertőzöttek maximális számát, és zárójelben látható, hogy ezekben az esetekben a tetőzés hányadik napra várható. Látható, hogy a szigorítás nélküli 47 naphoz képest (lásd a korábbi cikket) a tetőzés 2 hetes jól időzített kijárási tilalom esetén például 3 héttel kitolódik, és persze el is húzódik, ahogy azt korábban láttuk.
Mindezekből kitűnik: elképzelhető, hogy a kormány azért nem rendelte még el a kijárási tilalmat az egész országra, mert ezt még talán nem érdemes meglépni. Ettől függetlenül azonban bármilyen önkarantén és önmérséklet csökkenti a fertőzés növekedési rátáját, és segíti a járvány kevésbé drasztikus lefolyását.
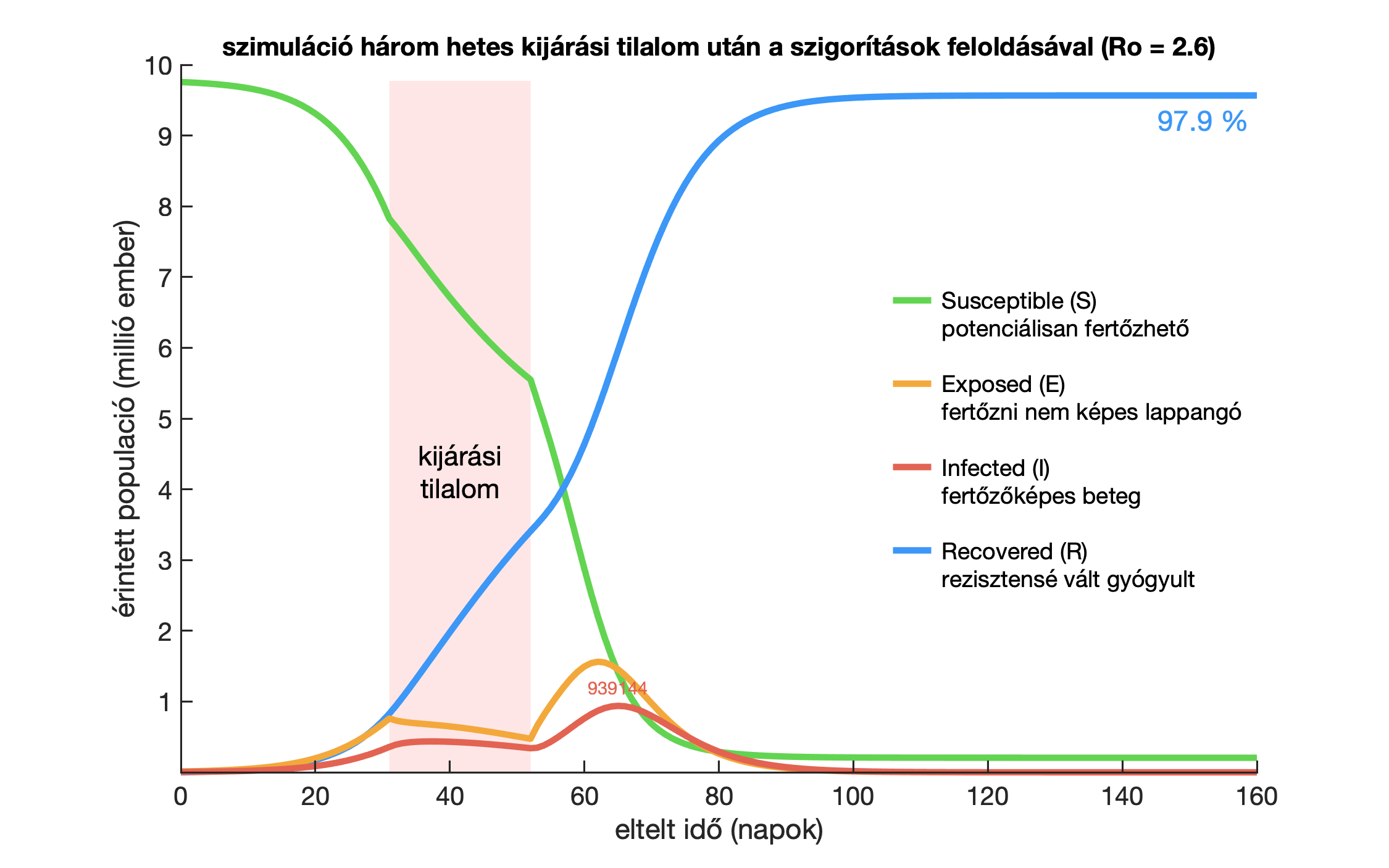
A fegyelemre ráadásul egy esetleges kijárási tilalom bevezetése után is szükség van. Ha a tilalom után rögtön visszaállnánk a rendes kerékvágásba, és nem hagynánk meg a jelenleg is érvényes rendelkezéseket (iskolabezárások, rövidített nyitva tartás, betiltott rendezvények, stb.), akkor a kijárási tilalom hatása szinte nem is tudna érvényesülni, és a járvány új erőre kapna. Ezt mutatja az alábbi szimuláció, ahol az optimálisan időzített háromhetes kijárási tilalom után eltöröljük a rendelkezéseket, és feltételezzük, hogy a találkozásaink és az elővigyázatlanságunk (azaz a β paraméter) megkétszereződik. Ennek hatása az, hogy a fertőzöttek száma is legalább megkétszereződik, és végül olyan számnál tetőzik (lásd piros szám, 940 ezer), ami a kijárási tilalom nélkül is előállt volna.
Természetesen, ahogy azt korábban is elmondtuk, a fenti modellek csak modellek, nem írják le teljes mértékben a valóságot, így azokkal csak a folyamatok befolyásolhatóságát szerettük volna szemléltetni, illetve megmutatni, hogy egyáltalán nem triviális kiválasztani egy nagyon szigorú kijárási tilalom elrendelésének megfelelő időpontját, illetve annak időtartamát.
A modell korlátaira továbbra is érvényesek a korábbi cikkben leírtak, és azokhoz még érdemes hozzátenni, hogy a tetőzés idején, amikor a betegek jelentős része szorul kórházi ellátásra, különösen nehéz a modellezés, ekkor ugyanis a kórházi dolgozókat külön érdemes modellezni eltérő szerepük és találkozási-érintkezési szokásaik miatt.
Jelenleg a kutatók számára a legfontosabb a reális fertőzési ráta megbecslése annak érdekében, hogy minél pontosabbak legyenek a jóslatok, és ezáltal segíteni tudják a kormányt a helyes döntések helyes időzítésében. Ehhez azonban a hazai körülményekre vonatkozó kutatások szükségesek. Nagy segítséget jelent, ha minél többen kitöltitek a kutatók által készített kérdőívet, amit korábban már közöltünk. Köszönjük!
A szerző fizikus.
Kapcsolódó cikkek a Qubiten:
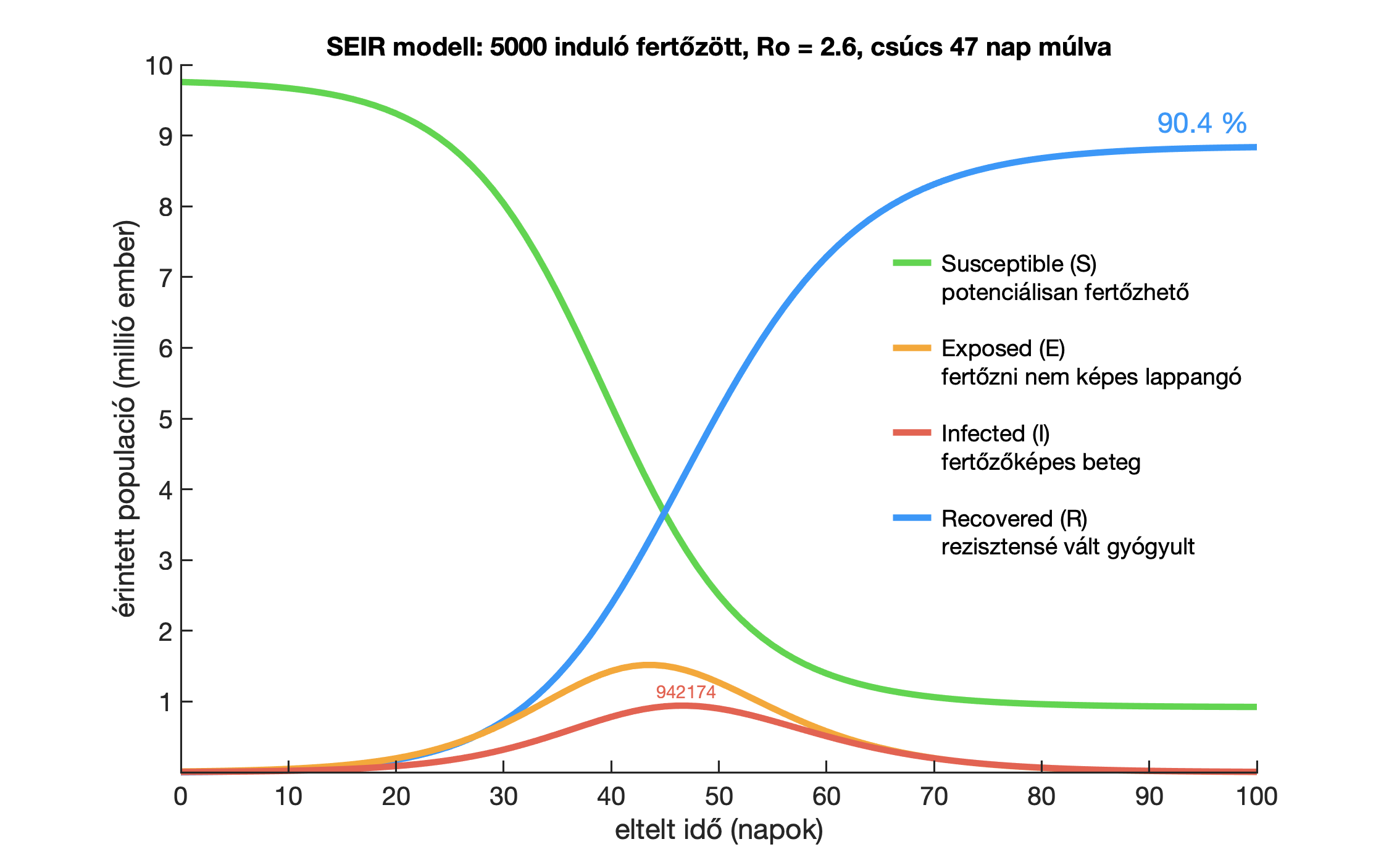
Milyen messze van a járvány csúcsa Magyarországon, és hogyan tudjuk ezt modellezni?
A SEIR modell a fertőzésre fogékonyak, a fertőzöttek és a betegek száma mellett figyelembe veszi a lappangó eseteket is. Az eredmény attól függ, hogy ebben a pillanatban hány fertőzött van az országban, és mennyi az R0, vagyis a reprodukciós ráta.
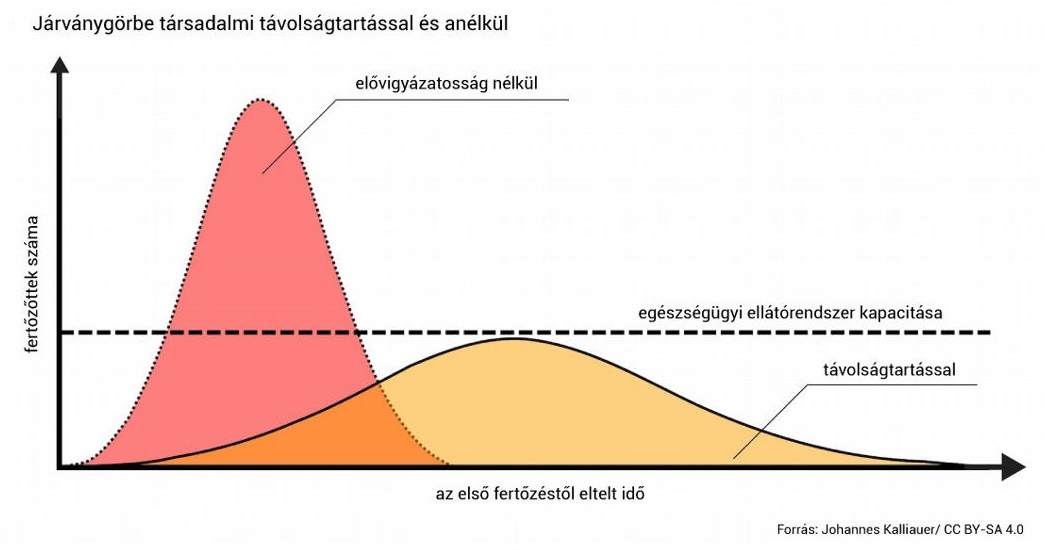
Mi az a hírhedt járványgörbe, és helyesen járunk-e el, ha megpróbáljuk kilapítani?
Joscha Bach, a mesterséges intelligenciával foglalkozó amerikai AI Foundation kutatója amellett érvel, hogy a görbe ellaposítása nem fog működni, és nem a görbét kell kilapítani, hanem a járványt kell megállítani. Igaza van, de ez nem változtat a jelenleg alkalmazandó intézkedéseken. Lássuk, miért!
A járványdinamika segít abban, hogy megértsük, miről szólnak a mostani intézkedések
Minél kisebb az egyszerre jelentkező esetszám, annál kevésbé van leterhelve az egészségügy. A jelenlegi intézkedések ezt az időbeli elhúzást kívánják elérni, amivel a járvány időtartamát kitolják ugyan, de az egészségügy leterheltségét csökkentik.
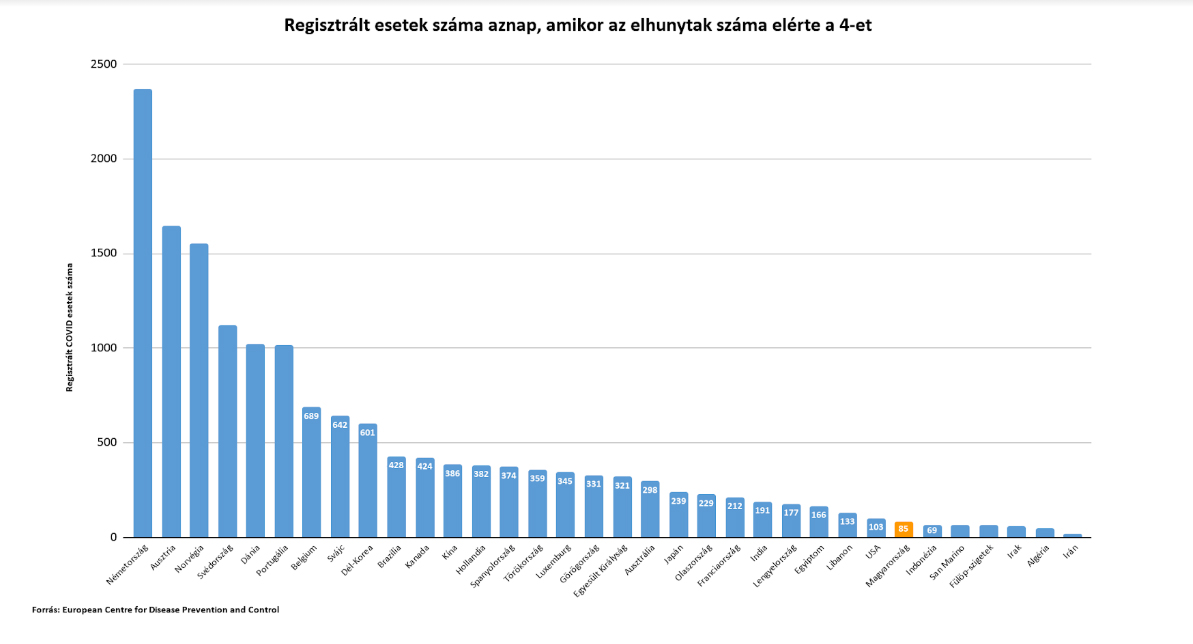
Magyarország túl kevés tesztet végez, és kifejezetten rosszul áll a vírusos esetek felderítésében
A 8 milliós Ausztriában eddig ötször, a 11 milliós Csehországban négyszer, a 2 milliós Szlovéniában háromszor annyi tesztet végeztek, mint Magyarországon, a feleakkora népességű Szlovákiában és az ötödakkora Észtországban pedig nagyjából ugyanannyit. Hogy ez miért baj?