Nincs nyoma, hogy a halála előtt pár nappal még az ősrobbanás előtti idők mibenlétéről nyilatkozó Stephen Hawkinghoz eljutott-e a Physical Review Letters idei harmadik számában megjelent tanulmány. Pedig sokat elárult volna, hogy a népszerűségénél is nagyobb jelentőségű tudományos örökséget hátrahagyó elméleti fizikus mit reagál arra a frappáns levezetésre, amely szerint bizonyos fekete lyukak nem pusztítanák el az őket közelről tanulmányozókat. Az asztronauták akkor sem bomlanának atomjaikra – a Hawking 1988-as Az idő rövid története című bestsellerében felvázolt spagettifikáció (spaghettification) jelensége miatt gigantikus cérnametéltté nyúlva –, ha áthaladva az eseményhorizonton, belépnének a brutális gravitációs ár-apály erőknek kitett fekete lyukba. Ahelyett, hogy az extrém méretű gravitációs szingularitás felemésztené őket, csak a múltjukat törölné, a túloldalon pedig a múlt-jelen-jövő determinisztikus sorrendjétől eltérő öröklét lenne az osztályrészük.

A transzcendes sci-fikbe illő fekete lyuk-típust feltételező tanulmányról a kaliforniai Berkley honlapja számolt be elsőként – az érintett természettudományi szakok hallgatóira szabva az érthetőség szintjét. A doktori fokozatát ezen az egyetemen megszerző, jelenleg a tudományág egyik legnívósabb versenyistállójának tartott Clay Matematikai Intézet elit ösztöndíjasaként tevékenykedő német Peter Hintz a beavatatlanokra is gondolhatott, amikor úgy fogalmazott: „olyan matematikai kérdést feszegetünk, amelynek a fizikai és a filozófiai vetülete is kúl”.

A feszegetés azért is különleges, mert a feketelyuk-specialista matematikusokból, elméleti és asztrofizikusokból álló társaság a ma ismert univerzum evolúcióját tökéletesen leíró, a 2016-ban detektált gravitációs hullámok létét is megjósoló általános realativitáselméletből vezette le modelljét.

Albert Einstein 1915-ben publikált kozmológiai alapvetésének laikusok által is megérthető lényege, hogy egy tömegpont mellett elhaladva a fény a tér görbületét követve elhajlik. Az általános relativitáselmélet nyomán pár év múlva megalkotott úgynevezett Einstein-egyenletek pedig azt fejezik ki, hogy miképpen lehet matematikailg leírni azt, amikor az anyag meggörbíti maga körül a teret. Ezek egyike az úgynevezett Reissner–Nordström-metrika, amellyel leírhatóak a gömbszimmetrikus fekete lyukak. Hintz és kollégái szerint a múlt nélküli örökléttel kecsegtető galaktikus objektumok is ilyenek:

link Forrás

A tanulmány egyik hivatkozási alapja a Roger Penrose által az 1960-as évek végén felvázolt kozmikus cenzor teória, amely szintén frappáns, de matematikailag kidolgozatlan magyarázata a fekete lyukak működésének. A Hawking és a nála több mint tíz évvel idősebb Penrose által közösen felállított Penrose-Hawking tétel szerint az általános relativitáselmélet mozgásegyenletének minden megoldásában létezik a bármit elpusztító szingularitás. Hogy ne legyen ilyen egyszerű, maga Hawking lepte meg a tudományos világot alig pár évvel később azzal, hogy a fekete lyukak mégsem mindent elnyelő kozmikus csapdák. A jórészt összeomló csillagokból keletkező, a fényt is rabul ejtő rejtélyes objektumok által kibocsátott Hawking-sugárzás létét 1974-es publikálása óta vitatják, de egzakt cáfolattal mindmáig nem szolgált senki.

Penrose kidolgozott egy módszert arra is, hogy a fekete lyukakat körülvevő téridőtartományokat matematikailag leképezhesse. A Penrose-diagramnak nevezett metódus lehetővé teszi a fekete lyuk felé közeledő objektumra ható gravitációs effektusok szemléletes ábrázolását. Így valahogy:

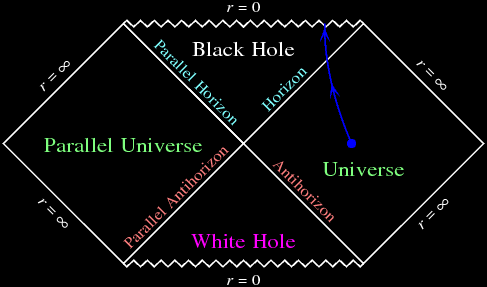
A szingularitás következménye az általános relativitáselméletnek, de a valóságban még nem figyelte meg senki. Penrose is kétféle kozmikus cenzort vázolt fel annak idején. Az egyik a mindent felfaló fekete lyukakat feltételezi, kizárva minden más eshetőséget, a másik viszont megengedőbb. Peter Hintz – akinek mestere nem mellesleg Vasy András, a Stanford magyar matematikaprofesszora – erre alapozott csapatával. Állításuk szerint megtalálták, és tanulmányukban ki is fejtik az elméleti lehetőségét annak az átjárónak, amely a múlt által determinált jövő egyirányúságával jellemezhető univerzumból átvezet olyan párhuzamos valóságba, ahol nincs efféle determináció.

Ami elméletileg helytálló, nem biztos, hogy létezik

„A fizika nem lehet meg egyenletek nélkül, mert ez segít, hogy kvantitatív információt nyerjünk a külső világról. Előfordul, hogy az így nyert egyenletünk többletet ad arról a fizikai valóságról, mint amit eredetileg meg akartunk érteni. Erről a többletről később kiderülhet, hogy tényleg új ismeretet ad fizikai világunkról, de az is lehet, hogy ezt semmilyen tapasztalat sem igazolja vissza” – kommentálta kérésünkre a tanulmányról beszámoló cikkeket Rockenbauer Antal, a BME és az ELTE elméleti fizikus professzora.

Szerinte elég a megértéshez a középiskolás tanulmányok okán közismert másodfokú egyenletekre gondolni, amelyeknek a helyesen kívül értelmezhetetlen, hamis megoldásai is vannak. „Ez fokozottan érvényes Einstein gravitációs egyenletére. Az ok az egyenlet szerkezetében rejlik, amelyben az úgynevezett energia-impulzus tenzor kapcsolódik a téridő görbületét leíró metrikához. A gond az, hogy az energia és impulzus a metrikától függ, így a megoldás keresésekor először az ismeretlen metrika alapján kell felírni az energiát és impulzust, majd ebből kell meghatározni a görbületi adatokat. Evvel a metrikával kell újra számolni az energiát és impulzust, majd ismét meghatározni a téridő görbületeit. A módszer olyan, mintha ingoványba lépnénk, ahol nem érzünk a lábunk alatt szilárd talajt, és miközben ki akarunk onnan kerülni, mozgásunkkal megváltoztatjuk az ingovány szerkezetét, és még mélyebbre süllyedünk” – fogalmaz a professzor.

„A gravitációs egyenletet olyan körülmények között vizsgálva, ahol nagy a tömegsűrűség, könnyen alakulnak ki szingularitások, és végtelen görbület jöhet létre. A téridő szerkezete annyira megváltozik, hogy már nem tudunk többé különbséget tenni múlt és jövő között” – mondja a professzor.

Rockenbauer szerint az Einstein-féle gravitációs egyenlet kétségtelenül a fizika egyik csúcspontja, mivel nemcsak a Newton-féle törvény kis korrekcióját adta, hanem felhívta a figyelmet a fekete lyukak és a gravitációs hullámok létezésére, és magyarázta a csillagászati praxisban kozmikus léptékű nagyításokra használt gravitációs lencsehatást. A fizikus egyúttal azonban figyelmeztet: „Az egyenlet minden sikere ellenére fogadjuk azonban mértéktartással az olyan eredményeket, amelyek ellentétesek a józan ésszel és nem találkoznak – legalább is egyelőre – tényleges megfigyelésekkel”.