Karikó Katalinnak és a Gömböcnek köszönhető a forradalmi amerikai találmány, a lenyelhető vakcina
Az új koronavírus elleni egyik első vakcinával 2020-ban állt elő az amerikai Pfizer és a németországi Biontech konzorciuma. Az oltóanyag a Nobel-díjra is esélyesnek tartott Karikó Katalin és Drew Weissman által 2005-ben szabadalmaztatott mRNS-technológiának köszönhető. A hírvivő RNS terápiás alkalmazásához szükséges kutatásokat a magyar biokémikus 1990-ben kezdte meg az Egyesült Államokban.
Karikótól teljesen eltérő területen tevékenykedik Domokos Gábor, aki 1995-ben kezdett dolgozni a legendás orosz matematikus, Vlagyimir Igorevics Arnold sejtésén, amely a négynél kevesebb egyensúlyi pontú testek létezését jósolta meg. Az elméleti lehetőséget végül 13 évvel később 2008-ban bizonyította az alkalmazott matematikus a Várkonyi Péterrel közösen megalkotott, Gömböcként ismert két egyensúlyi pontú mono-monostatikus új geometriai formával. A Gömböc eleinte csupán egy érdekes tudományos eredmény volt, és a feltalálóknak sokáig elképzelésük sem volt arról, hogy a játékos forma használható lesz-e egyáltalán valamire.
Az mRNS-technológiában és a Gömböc felfedezésében látszólag nem sok közös pont van. Nemrégiben azonban kiderült, hogy a világhírű amerikai műszaki egyetem, a Massachussets Institute of Technology (MIT) tudósai a két egymástól igencsak távol eső tudományterületen folytatott alapkutatásokat felhasználva fejlesztették ki a kapszulaként lenyelhető mRNS-vakcinájukat.
Robert Langer vegyészmérnök és Giovanni Traverso gasztroenterológus január végén publikálták azt a több alapkutatási eredményt ötvöző tanulmányukat, amelyben bemutatták forradalmi vakcinafejlesztésük legújabb eredményét. Azt az áfonya méretű, a gyomorban még nem lebomló anyagból készült kapszulát, amely egyedi súlyelosztása miatt kizárólag a gravitációra hagyatkozva egy olyan stabil helyre navigálja magát a gyomorban, ahonnan az mRNS-vakcina biztonsággal beinjektálható a gyomorfalba.
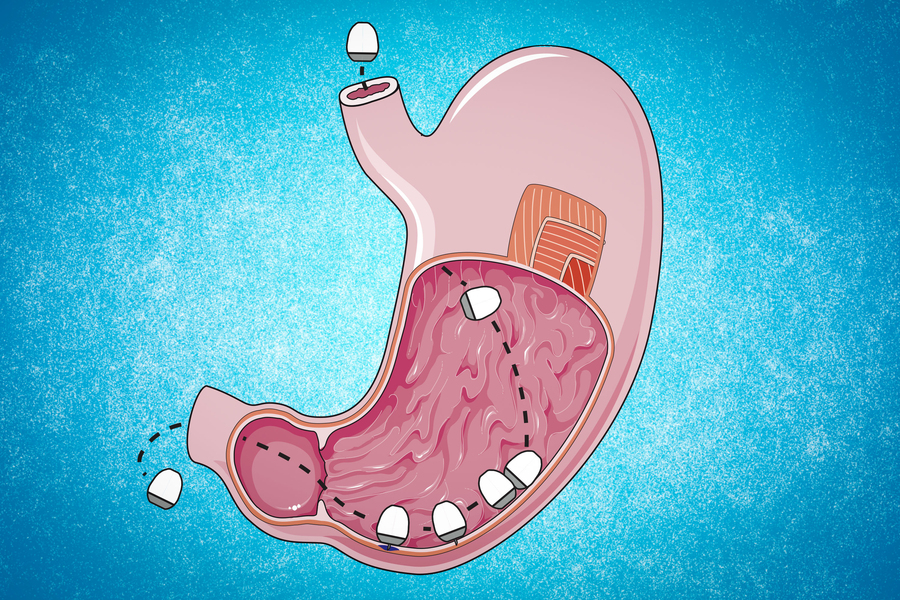
Az MIT kutatói természetesen nem titkolják, hogy nem csak saját eredményeiket használják munkájukhoz. Január végén publikált cikkükben hivatkoznak arra a tanulmányra, amelyben Karikó Katalin és kollégái 2014-ben felvázolták a még kísérleti fázisban lévő mRNS-technológiájukban rejlő terápiás lehetőségeket. Langer és Traverso ugyanígy járt el a Domokos Gábor és Várkonyi Péter, a BME Építészmérnöki Kar szilárdságtani és tartószerkezeti tanszékének oktatói által írt 2007-es dolgozattal is, amelyben a szerzők a teknőspáncél alakjának morfológiáját tárgyalva leírták annak a matematikáját, hogy miként képesek ezek a hüllők kizárólag a gravitáció révén a hátukról a talpukra billenni.
Karikó Katalin: A Gömböc itt van a polcomon
„Már jó ideje az érdeklődésünk középpontjában van az mRNS orális bevitele – válaszolta kérdésünkre Karikó Katalin. – Korábbi közleményekben már olvastam a különleges alakú kapszulákról, vagyis medical device-okról, amelyek nem tapadnak le a gyomorban, hanem továbbgördülnek. Azt hiszem ahhoz nem kell nagy fantázia, hogy megértsük, mennyi előnye van a szájon át adható vakcináknak az izomba szúrt vakcinákhoz képest. Nem kell az orvoshoz sem elmenni, mindenki maga be tudja venni. Az emberek sokkal inkább lenyelnek bármit is, mintsem megengedjék, hogy megszúrják őket. A vakcina elleni rezisztencia is sokkal kisebb orális esetben”.
Karikó szerint egyértelmű, hogy „a tudomány a kutatók tudásából építkezik. Állandóan ötleteket szerzünk mások munkáiból. A biológiában analóg folyamatokat keresünk, figyeljük, hogy különböző dolgokra van-e precedens. Ezért jó, ha valaki minél többet olvas a tudomány különböző területeiről. Mindezen ismeretek értékesek a hipotézis vezérelte kutatásoknál, sőt még az adathalmazok analízisének magyarázatainál is”.
Ami pedig az mRNS-technológia és a mono-monostatikus test nem várt találkozását illeti, arra Karikó azt írta, hogy „a Gömböc itt van a polcomon, és magam is sokat görgetem, hogy megértsem, miről is van szó”.
A Gömböc és a világegyetem
Domokos először csak csodálatosan szépnek találta a legendás orosz matematikus, Vlagyimir Igorevics Arnold sejtését, amelyben a négynél kevesebb egyensúlyi pontú testek létezését vetítette előre.
„Arnoldot ugyan matematikusként tartják számon, de ennél jóval tágabb értelemben volt zseniális tudós elme. Legfontosabb művei – például a Naprendszer stabilitásának leírása, vagy a róla elnevezett Arnold-diffúzió – a fizikához és a matematikához egyaránt kötődnek, hiszen utóbbi volt Arnold számára a természet nyelve. A Gömböcből kibontakozó, tizenöt éve fejlődő történet az ő egyik villanásának a sokszoros visszatükröződése” – mondja Domokos.
A számtalan műalkotás mellett a formájából fakadó talpra álló tulajdonsága ihlette a Pennsylvania Egyetem különleges, ütközések után is könnyen stabilizálódó helikopter drónjainak fejlesztését. Domokos szerint „az MIT is azért vette át a formát, hogy kapszulájuk a létező leggyorsabban, legkönnyebben álljon talpra. Ebben segíti az alján elhelyezett nehezék, de a formának is kulcsszerep jut. Az utóbbit addig optimalizálták, amíg kikötöttek a Gömböcnél, és ennek ismeretében szerkesztették meg a maguk turbó Keljfeljancsiját”.
Az alkalmazott matematikus úgy véli, hogy a Gömböc megtalálása a fentieken túl megvilágította azt is, hogy „lehet a számok nyelvén formákról beszélni, az élettelen természetet így lehet katalogizálni morfológiai alapon”. Mint mondja, másfél évtizede még senki sem sejtette, de az első ismert mono-monostatikus test felfedezése vezetett el az élettelen természet alakfejlődési folyamatainak egy általános leírásához.
Domokos és kollégái a Gömböcre épülő kutatásaikban ugyanis arra jutottak, hogy a folyó mosta kavicshoz és a szélben szálló homokszemcsékhez hasonló természetes formák eróziója során az egyensúlyi helyzetek száma végig csökken, és ilyen értelemben a Gömböc felé tartanak a formák, ám a végállapotot, vagyis a Gömböc formát soha nem érik el. „A kövek születésüktől kezdve folyamatosan kopnak, ez a kopási folyamat univerzális, az egész világegyetemben jelen van”.
A szuperszámítógépes matematikai modellezés és geológusokkal, geofizikusokkal végzett közös munka két éve arra is fényt derített, hogy ennek a formaevolúciós folyamatnak a kezdeti állapota, a töredezés is univerzális jelenség.
„A folyamat kezdőpontja az ideális platóni kocka, a vége pedig a Gömböc, és annak ellenére, hogy a természeti folyamatokban egyik sem jelenik meg, a folyamat kezdetét és végét jelző alapvető geometriai formákként sokat segítenek a folyamat megértésében. Az elméletnek köszönhetően a jelenben látott formák alapján meg tudjuk fejteni, hogy milyen folyamatok alakíthatták ezeket. A jelenből a jövőre és a múltra is tudunk következtetni”
– fogalmaz Domokos.
Így mutatták ki 2015-ben amerikai kutatókkal közösen azt is, hogy a Curiosity Mars-járó fényképein látható marsi kavicsokat évmilliókkal korábban egy folyó formálta a most ismert alakjukra.
Mintázatok mindenütt
Domokos figyelme az utóbbi időben a morfodinamika egy speciálisabb területe felé fordult. Kollégáival és hallgatóival az űrszondák által lefotózott mintázatok alapján próbálnak meg következtetéseket levonni a Naprendszer egyes égitestein zajló történésekről.
„A Plutóról vagy az Európáról csak fotóink vannak. Ami azokon látszik, azok alapján próbáljuk visszafejteni az ott lezajlott folyamatokat” – mondja az alkalmazott matematikus.
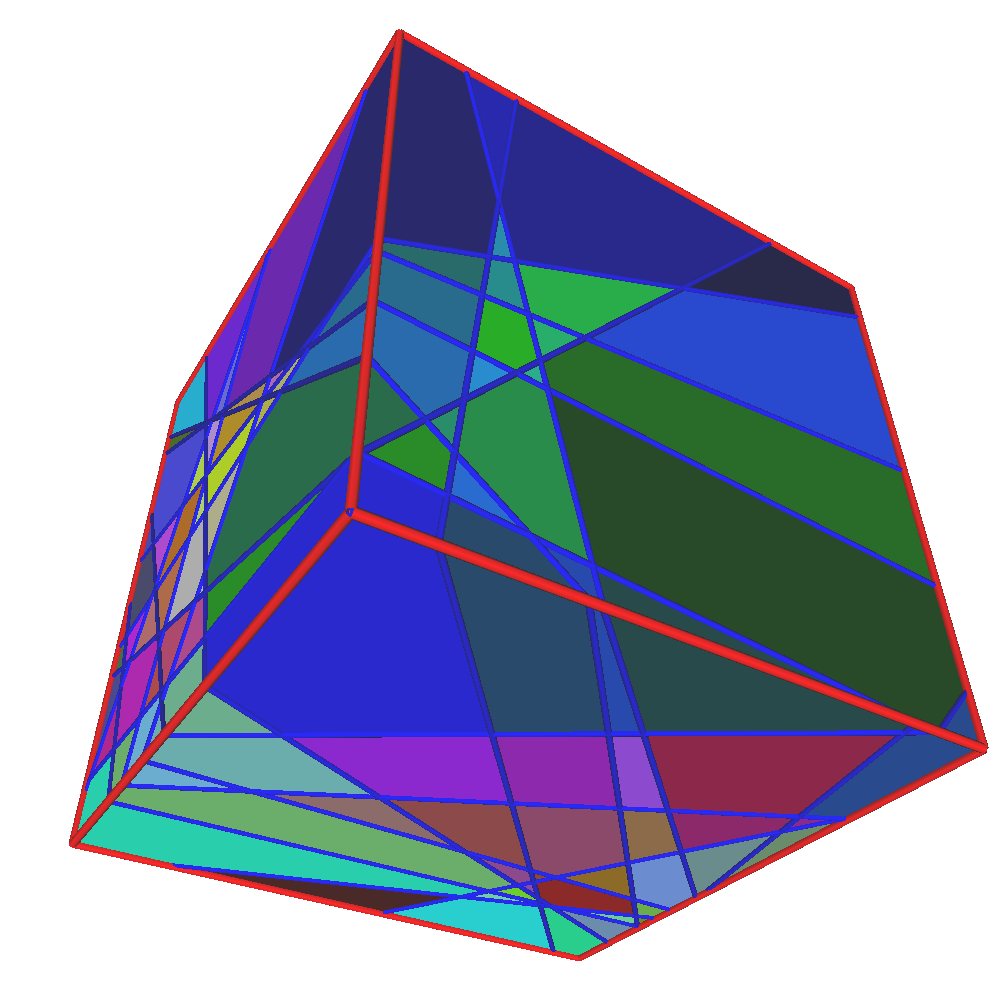
„Mivel még a Marson sincs fenn egyetlen 3D-s eszköz sem, ahhoz pedig kevés a fényképekben lévő adat, hogy hitelesen tudjunk 3D-vé alakítani azokat, ezért most a 2D mintázatokból indulunk ki, és azokból próbálunk következtetni a 3D mintázatokra is” – folytatja Domokos.
A fenti ábra Regős Krisztina végzős építészhallgató munkája, aki az MTA-BME Morfodinamika Kutatócsoport tagjaként Domokos témavezetésével jelenleg kiválósági diplomáját írja a 2D (és 3D) térkitöltő mintázatok témakörében, amelynek egyik célja a jelzett planetológiai kérdések tisztázása ezen eszközökkel.
Domokos úgy véli, hogy „bár a mintázatok tanulmányozása jelenleg még alapkutatásként zajlik, könnyen lehet, hogy az itt születő geometriai eredmények is később ipari fejlesztésekben fognak visszaköszönni”.
Korábbi kapcsolódó cikkeink:
