Mire jó egy járványmodell, és mire nem?

A Qubiten már ismertetett járványmodellek, a SIR és a SEIR akkor működnek a legjobban, ha nagyon nagy és alapvetően jól keveredő populációt modelleznek. Amikor semmilyen távolságtartási intézkedés nincs hatályban, és szabadon megyünk koncertre, moziba, vendéglőbe vagy kirándulni, a populáció igen jelentős része jól keveredik, és egy cseppfertőzéssel terjedő kórokozó szabadon terjedhet. Ebben az esetben a lakosság jelentős része megfertőződik, az egészségügyi rendszer sokszorosan túlterhelődik, és sokan meghalnak. Ennek belátására ez a modell elegendő.
A modell bonyolítható több korosztály figyelembe vételével, amelyek találkozási rátája vagy gyógyulási kilátásai különbözők. Az amerikai tudományos akadémia lapjában (PNAS) megjelent tanulmány például négy korosztályra bontja a népességet (0–19, 20–49, 50–64, 65+), a fertőző stádiumban lévő betegeknél pedig megkülönböztet enyhe tünetekkel rendelkezőket, súlyos tünetekkel rendelkezőket, nem-intenzív kórházi ápolásra szorulókat és intenzív ápolásra szorulókat. A nem kórházban gyógyulóknál külön kezeli azokat, akik betartják a karantén-előírásokat (az USA-ban szövetségi szinten nem rendeltek el kijárási korlátozást, de az egyes államok közül van, ahol igen) és azokat, akik nem. Egyébként azt találták, hogy a legfontosabb, hogy az enyhe tüneteket mutatók minél hamarabb vonuljanak karanténba. Ezzel csökkenhet leginkább a vírus továbbadása és így az egészségügy leterheltsége.
A kritikus infrastruktúra időbeli igényét nem adja jól vissza az egyszerű modell
Azt látjuk a világban, hogy a fő kérdés, hogy mennyi kórházi ágyra, intenzív ágyra és lélegeztetőgépre van szükség. Ez az a kritikus infrastruktúra, aminek hiánya korlátozhatja a gyógyító munkát. Ehhez ismernünk kell, hogy egy adott beteg hány napot tölt kórházban, illetve hány napig szükséges számára a mesterséges lélegeztetés.
Az alap S(E)IR modellben a gyógyulásnak van egy fix rátája, amely az egyes időintervallumokban meggyógyult betegek arányát mutatja százalékban. Azaz az egyes stádiumok közötti átmeneti valószínűség, például a gyógyulás valószínűsége független attól, hogy mennyi időt töltött egy adott személy abban az állapotban. A betegek száma pedig exponenciálisan csökken. Tegyük fel, hogy egy betegnek átlagosan 10 napig van szüksége kórházi kezelésre (Wang et al. 2020). Ebben az esetben a betegek 50 százaléka a 7. napon, 65 százaléka a 10. napon meggyógyul, és a 44. napon csökken 1 százalék alá a betegek száma. A modell szerint a gyógyulások 50 százaléka a 3. és a 13. nap közé esik, a kórházi adatok alapján viszont a 6. és a 12. nap közé, magyarán a valóságban a modellnél szűkebb intervallumba várjuk a gyógyulást, és például nem feltételezzük, hogy valaki másnapra felépül.
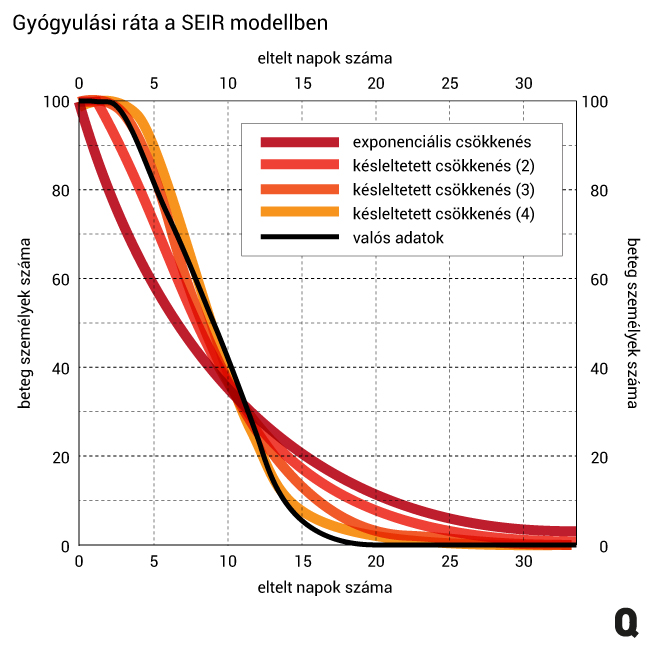
Egy tanulmány (Wearing et al. 2005) már 2005-ben felhívta a figyelmet arra, hogy az exponenciális eloszlással számolt inkubációs idő és gyógyulási idő erősen torzítja a járvány lefutásának becslését és az alkalmazható intézkedések kimenetelét. Megoldásként lehetséges, hogy a modellben további E (exposed, lappangó) és I (infected, fertőzött) állapotokat vezetünk be, amelyeken a fertőzötteknek át kell esniük, hogy végül az új stádiumba kerüljenek. Ilyen görbék láthatók a fenti ábrán (egy I állapot: exponenciális csökkenés, 2-3-4-szeres I állapot: késleltetett gyógyulás, kisebb szórás). A szegedi járványtanászok is ezt a módszert használták egy a COVID-19 járvány korai elterjedését modellező tanulmányukban (Boldog et al. 2020).
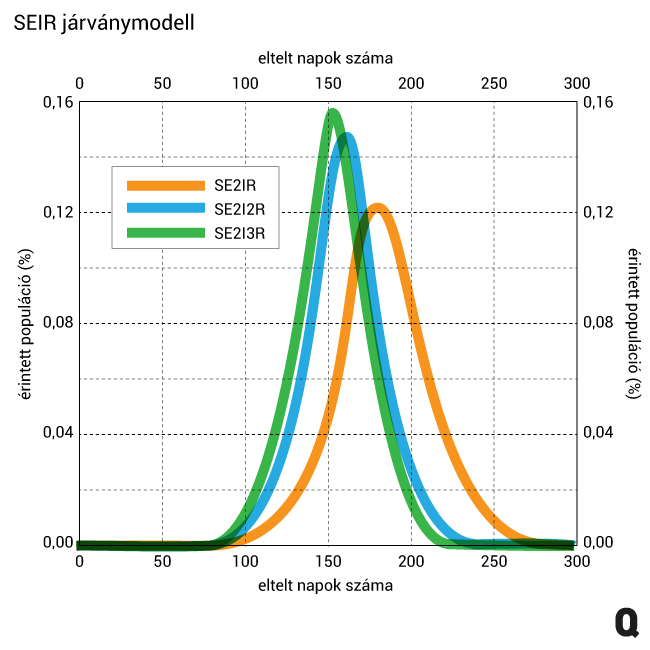
Egy modellben, amelyben két lappangó (E) állapoton és egy vagy több fertőző (I) állapoton keresztül számoljuk a járvány kiteljesedését (R0 = 2,2; lappangási idő 5,2 nap; gyógyulás ideje 10 nap) az összes megfertőzött száma nem változik, de a fertőzöttek számának a csúcsa igen. Minél szűkebb az az intervallum, amiben a valós gyógyulást várjuk (lásd fent az eredeti 3-13 nap helyett a reálisabb 6-12 napot), annál kisebb időintervallumra koncentrálódik a járvány tetőzése. Ez egyben azt is jelenti, hogy ilyenkor a csúcson a betegek száma akár több százezer emberrel több is lehet, cserébe a járvány gyorsabban lecseng.
A második járványhullámot okozhatja a rossz modell és a kívülről behurcolás is
A járvány lecsengésénél ütközik ki a S(E)IR modell újabb problémája, ami viszont nagyon technikai jellegű. Mivel az egyes állapotban levő emberek számát a modellben folytonos változóval (valós számmal) ábrázoljuk, így a számításokban elképzelhető, hogy tört mennyiségű fertőző van. Amikor egymillióan fertőzöttek, akkor ez lényegtelen. Viszont amikor kevés, mondjuk már csak 0,8 fertőzött van (akármit is jelentsen ez a valóságban), akkor ez probléma. A modellekben használt exponenciális csökkenés (amikor a nyájimmunitás vagy az intézkedés miatt az effektív reprodukciós ráta 1 alatti) végtelen idő múlva éri el a 0-át, a valóságos csökkenés ezzel szemben véges idő alatt megy végbe: egyszer vége lesz, és kész.
Vegyünk két megközelítést. Az egyik az alapeset, hogy folytonos változóval ábrázoljuk az egyes stádiumokban levő személyek számát. A másikban ezzel ellentétben kerekítjük az egyes stádiumokban levő emberszámot, tehát nem engedünk fél emberekkel való számolást. Mindkét modellben, amikor a betegek száma eléri a 10 százalékot (hogy látványos legyen a történés) az addigi 2,2-es reprodukciós rátát 0,9-re csökkentjük egészen addig, amíg 1 alá nem esik a fertőzöttek száma. Ezután a vírust – elméletben – újból szabadjára engedjük.
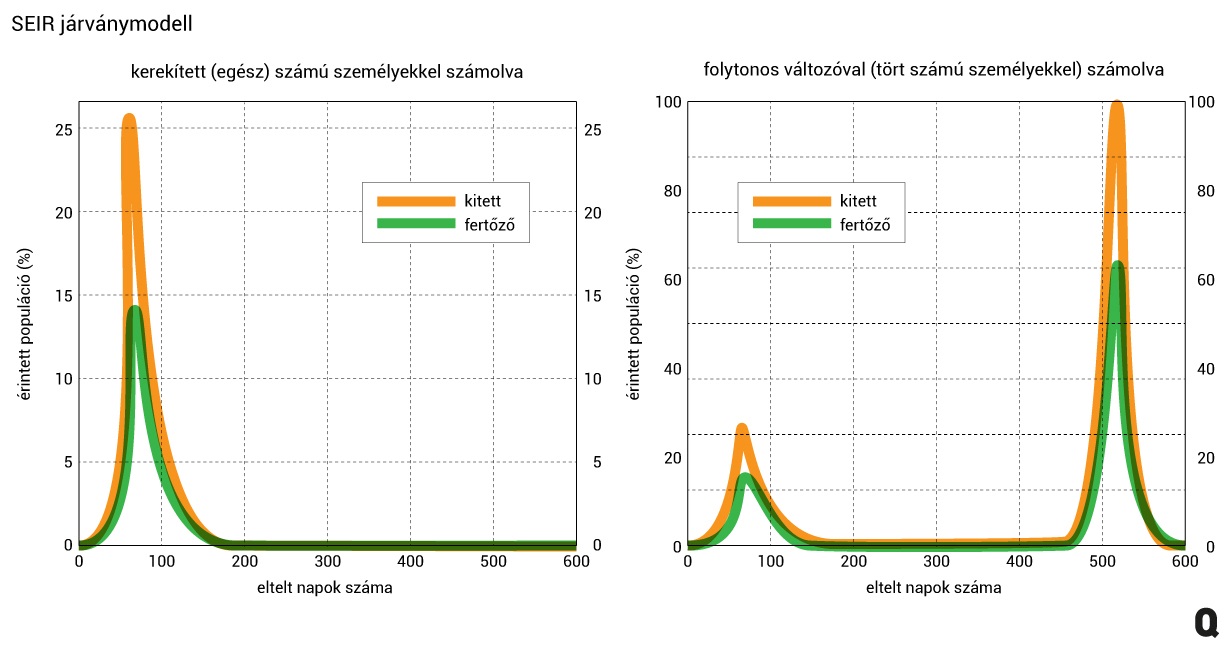
Az alap S(E)IR modellnél (jobbról) a járvány kiújul, mert 0,8 ember is képes fertőzni, és a modell egy második, még intenzívebb járványhullámot jelez előre. Ezzel szemben a valóságban (balról) nincs tört számú ember, és ilyenkor a járványnak vége van. Ahogy ebből is látszik, és mi is többször leírtuk, ezek a modellek sok embernél működnek jól, a járvány kezdetén és végén viszont tipikusan rosszul adják vissza a történéseket.
A kiújulás lehetőségével minden ország számol. Nem azért, mert rossz modellt használnak, hanem mert pontosan tisztában vannak a modellek még egy fontos korlátával: azzal, hogy egy zárt rendszerre vonatkoznak. Az országok, államok viszont nem zárt rendszerek: emberek mennek ki és be, még jelenleg is, hiszen a nemzetközi fuvarozás nem állt le – ráadásul a korlátozások is véget fognak érni egyszer. És ahogy Kínában, Dél-Koreában vagy épp Szingapúrban láttuk március végén–április elején, hiába a nagyszerű védekezés, ha az új esetek zöme kívülről érkezik. A modellek belföldre vonatkoznak, a járvány kívülről bármikor újraindulhat.
A szerző biológus kutató.
Kapcsolódó cikkek a Qubiten:
Jó ötlet szándékosan szabadjára engedni a járványt úgy, hogy csak az időseket zárjuk karanténba?
Nem jó ötlet. Hogy miért?
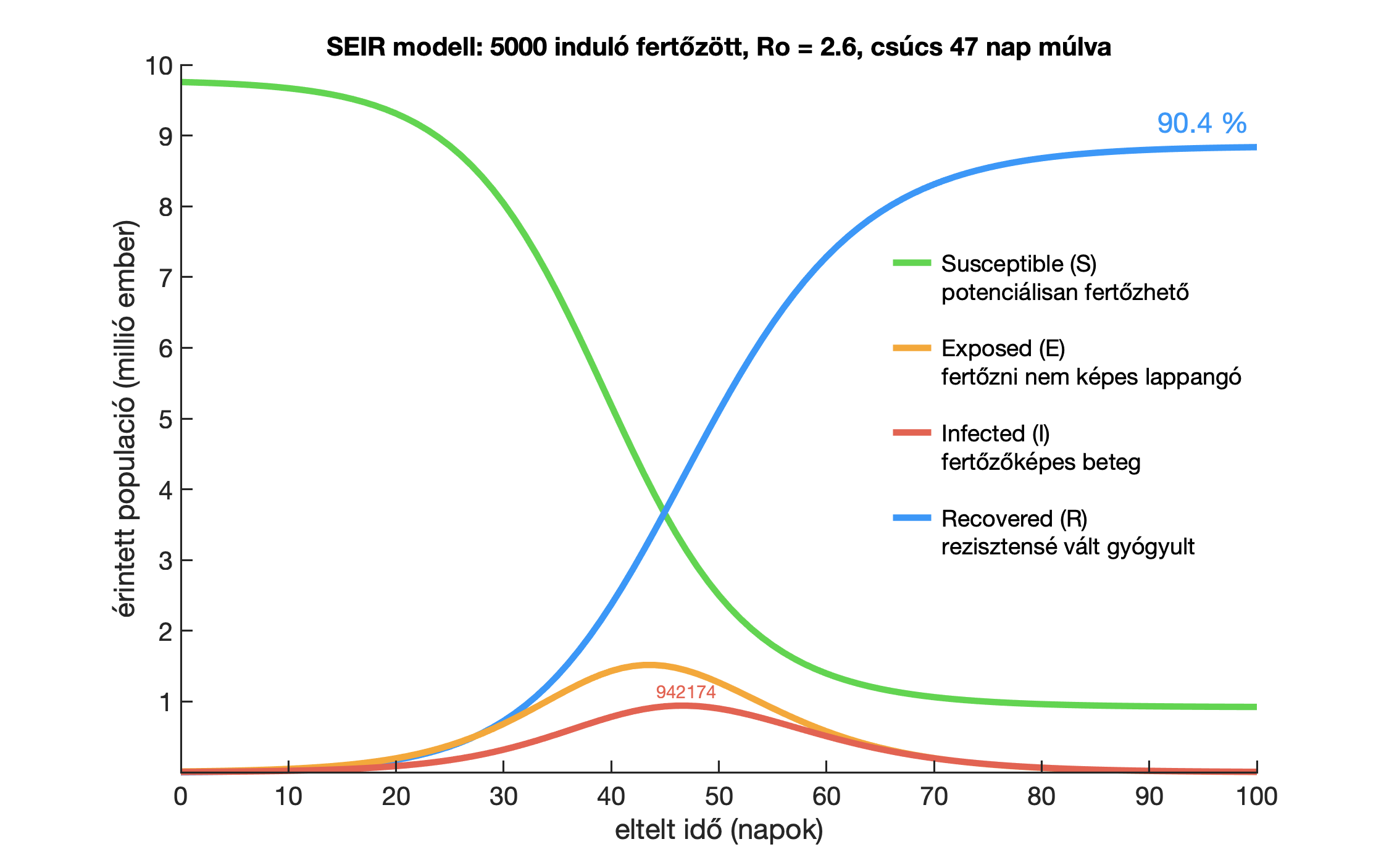
Milyen messze van a járvány csúcsa Magyarországon, és hogyan tudjuk ezt modellezni?
A SEIR modell a fertőzésre fogékonyak, a fertőzöttek és a betegek száma mellett figyelembe veszi a lappangó eseteket is. Az eredmény attól függ, hogy ebben a pillanatban hány fertőzött van az országban, és mennyi az R0, vagyis a reprodukciós ráta.

A koronavírus, a pöröly és a tánc
A pöröllyel (hammer) lecsapunk a vírusra, a többit meg majdcsak kimozogjuk valahogy (dance). Az első fázisban a legfontosabb a gyorsaság és a fertőzöttek elszigetelése, a másodikban az, hogy a korlátozásokat és a járvány dinamikáját olyan egyensúlyban tartsuk, hogy a fertőzöttek száma ne kezdjen újra exponenciálisan növekedni.
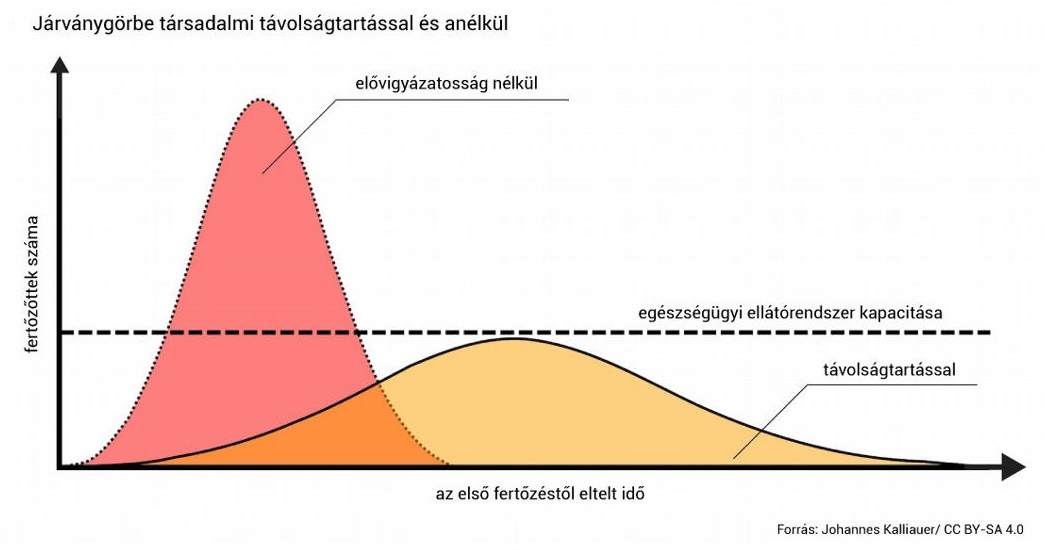
Mi az a hírhedt járványgörbe, és helyesen járunk-e el, ha megpróbáljuk kilapítani?
Joscha Bach, a mesterséges intelligenciával foglalkozó amerikai AI Foundation kutatója amellett érvel, hogy a görbe ellaposítása nem fog működni, és nem a görbét kell kilapítani, hanem a járványt kell megállítani. Igaza van, de ez nem változtat a jelenleg alkalmazandó intézkedéseken. Lássuk, miért!
A járványdinamika segít abban, hogy megértsük, miről szólnak a mostani intézkedések
Minél kisebb az egyszerre jelentkező esetszám, annál kevésbé van leterhelve az egészségügy. A jelenlegi intézkedések ezt az időbeli elhúzást kívánják elérni, amivel a járvány időtartamát kitolják ugyan, de az egészségügy leterheltségét csökkentik.
Kapcsolódó cikkek